区间dp

一.什么是区间dp?
顾名思义：区间dp就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的 最优解进而得出整个大区间上最优解的dp算法。

二.核心思路既然让我求解在一个区间上的最优解，那么我把这个区间分割成一个个小区间，求解每个小区间的最优解，再合并小区间得到大区间即可。所以在代码实现上，我可以枚举区间长度len为每次分割成的小区间长度（由短到长不断合并），内层枚举该长度下可以的起点，自然终点也就明了了。然后在这个起点终点之间枚举分割点，求解这段小区间在某个分割点下的最优解。

for(int len = 1;len<=n;len++){//枚举长度
        for(int j = 1;j+len<=n+1;j++){//枚举起点，ends<=n
            int ends = j+len - 1;
            for(int i = j;i<ends;i++){//枚举分割点，更新小区间最优解
                dp[j][ends] = min(dp[j][ends],dp[j][i]+dp[i+1][ends]+something);
            }
        }
    }

(1)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动相邻的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。

这是石子归并的简化版本，石子处于一排。由于发现只能是相邻的2堆石子进行归并。我们会发现，贪心算法在此处便失去作用，局部最优解并不能带来整体最优解。

因此，不难让我们想到，此题应该采取DP(dynamic Programing)来求其最优解。

动态规划常常采取从部分整体最优解的拆分来得到最优解法的递归式，我们可以想到，此处是由2堆石子合并，所以最终最优解肯定是由两个局部最优解的加上整体的和求得。

因此，我们可以推断出动态转移方程：

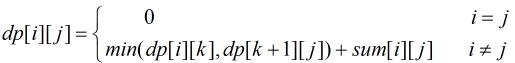
dp[i][j]在此处表示从第i堆加到第j堆的最优解，而当i == j是，并不存在相加，所以结果为0

#include <iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define INF 0x3f3f3f
int stone[105];
int dp[105][105];
int sum[105];
int main()
{
    int n;
    scanf("%d",&n);
    memset(sum,0,sizeof(sum));
    memset(dp,INF,sizeof(dp));
    for(int  i =1;i<=n;i++){
        scanf("%d",&stone[i]);
        sum[i] = sum[i - 1] + stone[i];//重量
        dp[i][i] = 0;
    }
    for(int len = 1;len<=n;len++){//枚举长度
        for(int j = 1;j+len<=n+1;j++){//枚举起点，ends<=n
            int ends = j+len - 1;
            for(int i = j;i<ends;i++){//枚举分割点
                dp[j][ends] = min(dp[j][ends],dp[j][i]+dp[i+1][ends]+sum[ends]-sum[j-1]);//更新状态
            }
        }
    }
    cout<<dp[1][n]<<endl;
    return 0;
}

推广到环形的石子合并问题：


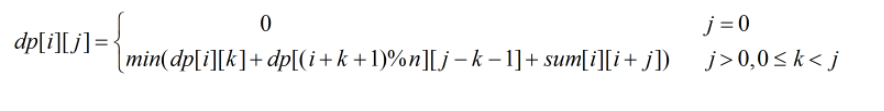
不过，此处的j与前面(1)中的j意义并不一样，此处的j意义为：从第i堆出发，往下数j堆石子。
因此，j == 0时，自然dp[i][j] == 0了
因为j的意义不同，所以dp[i][j]长得自然不一样了，实际上还是一个意思。
所以sum[i][j]也改为：

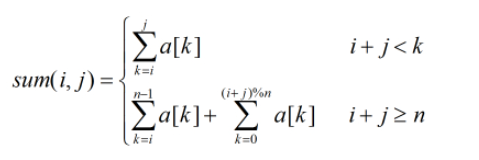
#include <iostream>
#include <algorithm>
#include <limits>
using namespace std;
const int INF = INT_MAX;
const int maxn = 1003;
int dp[maxn][maxn];
int stone[maxn];
int sum[maxn]; //0 - i 的和
int n; //本次的个数
int getSum(int i, int j) {
    if (i + j >= n)
        return getSum(i, n - i - 1) + getSum(0, i + j - n);
    else
        return sum[i + j] - (i > 0 ? sum[i - 1] : 0);
}
int findMin() {
    for (int i = 0; i < n; i++) {
        dp[i][0] = 0;
    }
    for (int j = 1; j < n; j++) {
        for (int i = 0; i < n; i++) {
            dp[i][j] = INF;

            for (int k = 0; k < j; k++) {
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[(i + k + 1) % n][j - k - 1] + getSum(i, j));
            }
        }
    }
    return dp[0][n - 1];
}

int main() {
    while (cin >> n) {
        for (int i = 0; i < n; i++) {
            cin >> stone[i];
            sum[i] = 0;
        }
        sum[0] = stone[0];
        for (int i = 1; i < n; i++) {
            sum[i] = sum[i - 1] + stone[i];
        }
        cout << findMin() << endl;
    }
    return 0;
}