数学问题——组合数

1 求n!中有多少个质因子p

1.1 以10!中质因子2的个数为例

设n!中的质因子p的个数为f(n, p)

f(10, 2) = (10 / 2) + f(10/2, 2) = 5 + f(5, 2)

f(5, 2) = (5 / 2) + f(5/2, 2) = 2 + f(2, 2)

2! = 1*2 =                   f(2, 2) = (2/2) + f(2/2, 2) = 1 + f(1, 2) = 1 + 0 = 1

综上，f(10, 2) = 5+2+1 = 8

1.2 结论

        n!中质因子p的个数，实际上等于1~n中p的倍数的个数  加上  中质因子p的个数

// 计算 n! 中有多少个质因子p
int cal(int n, int p){
    if(n<p) return 0;  // n<p时1~n中不可能有质因子p
    return n/p + cal(n/p, p);
}

2 组合数的计算

2.1 组合数的基本概念

        是指从n个不同元素中选出m个元素的方案数(m<=n)

        

        

        

2.2 计算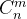

2.2.1 通过递推公式计算

        可以转换为下面两种选法的方案数之和：一是不选最后一个数，从前n-1个数中选m个数；二是选最后一个数，从前n-1个数中选m-1个数。于是得递推公式：

        用long long型存储结果，该方法在n=67、m=33时开始溢出

        该方法的时间复杂度为O(n^2)

// 递归代码
long long res[67][67] = {0};  // 将已经计算过的结果保存在数组中，可以减少重复计算
long long  C(long long n, long long m){
    if(m==0 || m==n) return 1;
    if(res[n][m] != 0) return res[n][m];
    return res[n][m] = C(n-1, m) + C(n-1, m-1);  // 赋值给res[n][m]并返回
}

// 或者是把整张表都计算出来的递推代码
const int n = 60;
void calC(){
    for(int i=0;i<=n;i++){
        res[i][0] = res[i][i] = 1;  // 初始化边界
    }
    for(int i=2;i<=n;i++){
        for(int j=0;j<=i/2;j++){
            res[i][j] = res[i-1][j] + res[i-1][j-1];    // 递推计算C(i, j)
            res[i][i-j] = res[i][j];  // C(i, i-j) = C(i, j)
        }
    }
}

2.2.2 通过定义式的变形来计算

只要能保证每次除法都是整除，就能用这种边乘边除的方法避免连续乘法溢出问题。

是个整数，显然每次除法都是整除。

时间复杂度为O(m)，在n=62、m=31时开始溢出

long long C(long long n,long long m){
    long long ans=1;
    for(long long i=1;i<=m;i++)
        ans = ans*(n-m+i)/i;    // 注意一定要先乘在除
    return ans;
}

2.3 计算

 2.3.1 通过递推公式计算

适用场景：支持m<=n<=10^4，p<=10^9级别的数据范围

// 递归代码
int res[1010][1010] = {0};  // 将已经计算过的结果保存在数组中，可以减少重复计算
int C(int n, int m,int p){
    if(m==0 || m==n) return 1;
    if(res[n][m] != 0) return res[n][m];
    return res[n][m] = (C(n-1, m) + C(n-1, m-1)) % p;  // 赋值给res[n][m]并返回
}

// 或者是把整张表都计算出来的递推代码
const int n = 1001;
void calC(){
    for(int i=0;i<=n;i++){
        res[i][0] = res[i][i] = 1;  // 初始化边界
    }
    for(int i=2;i<=n;i++){
        for(int j=0;j<=i/2;j++){
            res[i][j] = res[i-1][j] + res[i-1][j-1] % p;    // 递推计算C(i, j)
            res[i][i-j] = res[i][j];  // C(i, i-j) = C(i, j)
        }
    }
}

2.3.2 通过质因子分解来计算

适用场景：支持m<=n<=10^6，p<=10^9级别的数据范围

// 使用素数筛选法获得素数表prime，注意表中最大素数不得小于n
int prime[MAXN];
// 计算C(n,m)%p
int C(int n,int m,int p){
    int ans = 1;
    for(int i=0;prime[i]<=n;i++){
        // 计算C(n, m)中prime[i]的指数c, cal(n, k)为n!中含质因子k的个数
        int c = cal(n, prime[i]) - cal(m, prime[i]) - cal(n-m, prime[i]);
        // 快速幂计算prime[i]^c%p
        ans = ans *BinaryPow(prime[i], c, p) % p;
    }
    return ans;
}

2.3.3 Lucas定理

在p是素数的条件下，将m和n表示为p进制：

Lucas定理告诉我们下面等式成立：

这意味着将  分解为O(logn)级别个小组合数的乘积的模。

适用场景：p<=10^5且p为素数。支持m<=n<=10^18级别的数据范围

int Lucas(int n,int m){
    if(m==0) return 1;
    return C(n%p,m%p)*Lucas(n/p, m/p) % p;
}

        回忆进制转换部分，将10进制转换为p进制只需要不断除以p，然后对p取模即可