矩阵连乘问题

问题描述

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1， 2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次 序计算矩阵连乘积需要的数乘次数最少。

问题分析

对于一组相乘的矩阵列，满足如下性质，我们用(ri,rj)来描述一个矩阵

• 两个矩阵相乘必须满足第一个矩阵的列数等于第二个矩阵的行数也就是A(r1,c1)*B(r2,c2)，有C1=R2
• 新矩阵的规模是R1*C2，一组矩阵相乘后的规模是：R1*Cn
• 对于不同的结合次序，计算次数不同AB(CD)不一定等于A(BC)D,我们要找到一个划分次序使得计算的代价最小

算法分析

• 将矩阵连乘积 AiAi+1Ai+2…Aj简记为A[i:j] ，这里i≤j
• 考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵 Ak和Ak+1之间将矩阵链断开，i≤k<j，则其相应完全 加括号方式为
  
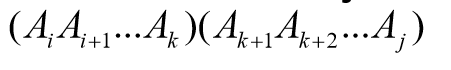
• 对于这样的一个划分，计算量是A[i:k]+A[k+1:j]+（A[i:k]*A[k+1:j]）
• 我们用P[0]，P[1].......P[n]来描述一个矩阵乘法列的行数和列数，也就是说：Ai的行数ri=P[i-1],ci=P[i]
• 根据最优子结构m[i:j]=m[i,k]+m[k+1,j]+pi-1*pk*pj

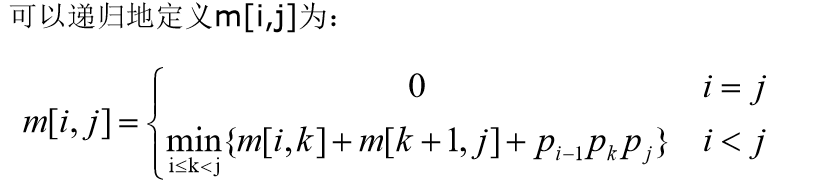
我们将会考虑递归实现和动态规划实现两种方法，并且对比复杂度

直接递归实现

#include <iostream>
using namespace std;
const int maxn=105,INF=0x7fffffff;
int P[maxn]={0};
int matrixChain(int i,int j)
{
    if(i==j) return 0;
    int minRes=INF;
    for(int k=i;k<j;k++)
    {
        int res=matrixChain(i,k)+matrixChain(k+1,j)+P[i-1]*P[k]*P[j];
        minRes=min(minRes,res);
    }
    return minRes;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<=n;i++)
        cin>>P[i];
    int res=matrixChain(1,n);
    cout<<res;
    return 0;
}

算法分析：

算法复杂度分析： 对于n个矩阵的连乘积，设其不同的计算次序为P(n)。 由于每种加括号方式都可以分解为两个子矩阵的加括号问题： (A1…Ak)(Ak+1…An)可以得到关于P(n)的递推式如下：

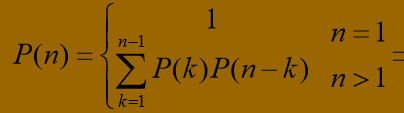
• 实际展开后我们发现这是一个卡特兰数列，其性质如下

• 我们使用其近似公式可知
  
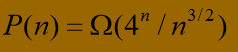
  显然这样的复杂度是不可接受的，我们可以对其进一步改进或者 使用动态规划，我么选用动态规划：

动态规划法

• 用数组m[n][n]存放A[i:j]的最佳结果
• 递推关系式：
  
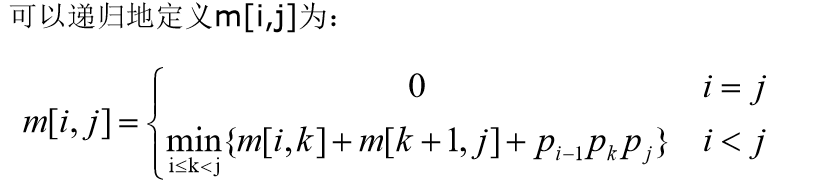
• 用数组S[n][n]记录结合律中的最佳划分
• 递推次序如下：
  
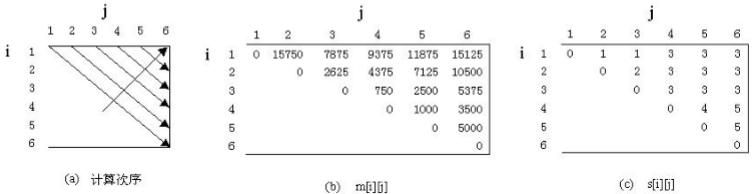
  代码如下：

#include <iostream>
using namespace std;
const int maxn=105,INF=0x7fffffff;
int P[maxn]={0},m[maxn][maxn]={0},s[maxn][maxn]={0};//初始化
void matrixChain(int n)
{//由于数组已经进行过初始化，所以预处理已经完成
    int res;
    for(int r=2;r<=n;r++)
    {//划分长度
        for(int i=1;i<=n-r+1;i++)
        {
            int j=i+r-1;//i到j的划分
            m[i][j]=INF;
            for(int k=i;k<=j-1;k++)//历遍r中所有的子划分
            {
                res=m[i][k]+m[k+1][j]+P[i-1]*P[k]*P[j];
                if(res<m[i][j])
                {
                    m[i][j]=res;//更新最小执行次数
                    s[i][j]=k;//更新结合律划分点
                }
            }
        }
    }
    printf("最小乘法次数=%d\n",m[1][n]);
}
void printS(int s[maxn][maxn],int i,int j)
{
    if(i==j) printf("A%d",i);//只有一个元素
    else{
        printf("(");
        printS(s,i,s[i][j]);//处理左划分
        printS(s,s[i][j]+1,j);//处理右划分
        printf(")");
    }
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<=n;i++)
        cin>>P[i];
    matrixChain(n);
    printS(s,1,n);
    return 0;
}

算法分析

算法matrixChain的主要计算量取决于算法中对r， i和k的3重循环。循环体内的计算量为O(1)，而3重 循环的总次数为O(n3)。因此算法的计算时间上界 为O(n3)。算法所占用的空间显然为O(n2)