【递归与分治基础详解】小白系列

1. 递归与分治的算法思想

• 将问题分解为k个子问题，对于这k个子问题进行求解；
• 如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题的规模足够的小，很容易求解为止。
• 将求出的小规模问题的解合并为一个更大规模的解，自底向上逐步求出原问题的解。

如果用一个图来表示递归以及分治算法思想的话，可以借鉴下图，其实其本质就是一个大事化小，小事化了的过程。

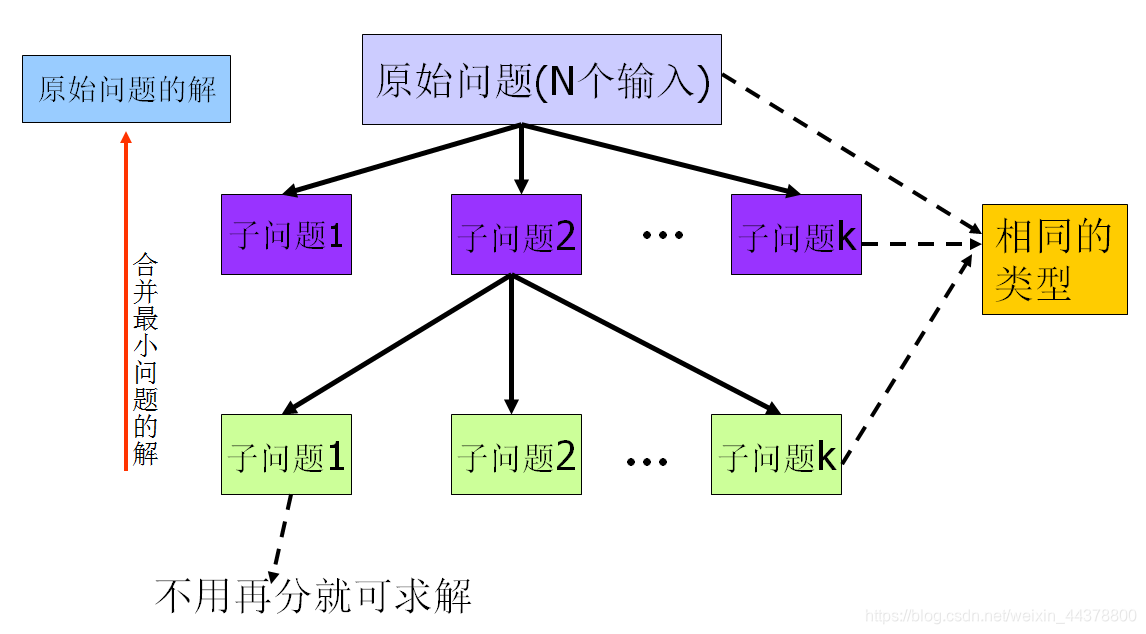
1.1 递归详解

首先我们来了解一下递归的一些特征：

• 直接或者间接调用自身的算法称为递归算法；用函数自身给出定义的函数称为递归函数；
• 由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生；
• 递归与分治像一对孪生兄弟，经常同时应用于算法设计中，并且由此产生了许多高效算法。

边界条件和递归方程是递归函数的两个要素

递归函数只有具备了这两个要素,才能在有限次计算后得到计算结果。

1.2 分治详解

分治法所能解决的问题一般具有以下几个特征：

• 该问题的规模缩小到一定程度就可以容易的解决；
• 该问题可以分解为若干个规模较小的相同的问题，即该问题具有最优子结构性质；
• 利用该问题的子问题的解可以合并求出该问题的解；
• 该问题所分解出的各个子问题是相互独立的，即各个子问题之间不包含公共的子问题。

最后一条特征涉及到分治法的效率，如果各个子问题不是独立的，则分治法需要做许多不必要的工作，重复的解公共子问题，这个时候动态规划会比分治法更加有效率。

分治法的伪代码如下所示：

divide-and-conquer(P)  {
    if ( | P | <= n0) adhoc(P);          //解决小规模的问题
    divide P into smaller subinstances P1,P2,...,Pk；//分解问题
    for (i=1,i<=k,i++)                            //参考全排列的子问题
        yi=divide-and-conquer(Pi);       //递归的解各子问题
    return merge(y1,...,yk);             //将各子问题的解合并为原问题的解
  }

在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。

2. 算法示例

在这一章节将主要展示一些示例，有一些代码是自己写的，有一部分直接摘自网上，摘抄部分会注明出处。

2.1 斐波拉契数列

2.1.1 解题思想方法

斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34 …

通过观察我们不难发现从第3项开始，每一项都等于前两项之和，从而我们可以得到斐波拉契数列的函数表达式：

然后我们不难可以写出斐波拉契数列的函数代码，这里用c++实现：

#include <iostream>

 int Fibonacci(int n) {
		if(n <= 0) {
			return 0;
		}
		if(n == 1 || n == 2) {
			return 1;
		}
		return Fibonacci(n -2) + Fibonacci(n-1);
	}

int main()
{
	std::cout << "result:" << Fibonacci(10) << std::endl;
}

2.1.2 缺点

其实在编写代码的过程中或者是自己手写推导计算的过程中，我们不难发现，计算的过程中有很多项都被重复计算，那么当n特别大的时候，很容易造成内存的溢出，于是在这个时候迭代算法可能会取得比递归更好的效果，参考此处。

在这里不难给出迭代的代码如下：

#include <iostream>

int FibonacciD(int n) {
		if(n <= 0) {
			return 0;
		}
		if(n == 1 || n == 2) {
			return 1;
		}
		int first = 1,second =1,third = 0;
		for(int i = 3; i<= n ;i++) {
			third = first + second;
			first = second;
			second = third;
		}
		return third;
	}

int main()
{
	std::cout << "result:" << FibonacciD(10) << std::endl;
}

然后我们测试一下当n达到一千万的时候两个函数各自的运行时间，依次是递归以及迭代，可以看到的是当数目特别大的时候，使用递归算法确实出现了内存溢出的问题而且运行时间也更长。

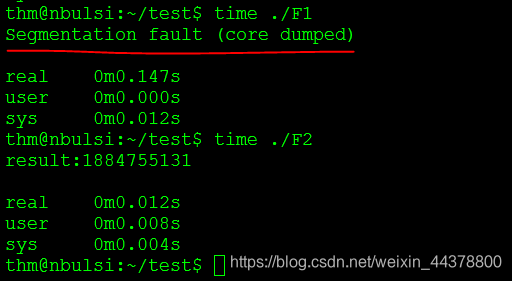
2.2 汉诺塔问题

2.2.1 问题描述

设a,b,c是3个塔座。开始时，在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,现要求将塔座a上的这一叠圆盘移到塔座b上，并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则：

规则1：每次只能移动1个圆盘；
规则2：任何时刻都不允许将较大的圆盘压在较小的圆盘之上；
规则3：在满足移动规则1和2的前提下，可将圆盘移至a,b,c中任一塔座上。

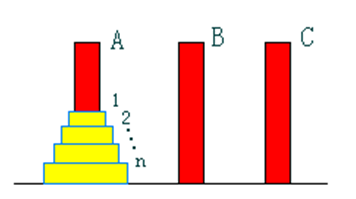
2.2.2 解题思路

如果说A只有三个圆盘的话，那么这种情况下是比较好推的，依次按照以下步骤就可以实现三个圆盘由A转到B上：

A–>B,A–>C,B–>C,A–>B,C–>A,C–>B,A–>B 总共7步就可以完成圆盘的换位，当达到n个圆盘的时候，可以分为以下几个步骤：

1. 将A（src）上n-1个圆盘借助B（dest）移动到C（rely）上；
2. 将A（src）剩下的一个圆盘移动到B（dest）上；
3. 利用A（src）将C（rely）上的n-1个圆盘移动到B（dest）上，此时变成了一个子问题。

代码如下，具体帮助理解为：

• n==1表示递归的终止条件
• 借助谁（rely）将谁的圆盘（src（source））移动到了谁那里（dest（destination）），这样子就能比较容易看懂代码了。

#include <iostream>
using namespace std;
 
void hanoi(int n ,char src, char dest,char rely)
{
    if(n == 1)
        cout << src << "-->" << dest << endl ;
    else
    {
        hanoi(n-1 , src, rely, dest) ;
        cout << src << "-->" << dest << endl ;
        hanoi(n-1 , rely, dest, src) ;
    }
}
 
int main()
{
    cout << "移动圆盘的顺序：" << endl ;
    hanoi(3, 'A' , 'B' , 'C') ;
 
    return 0;
}

可以得到最后结果为：

如果说将n的数目变大，例如4，则可以得到其他结果：

2.3 合并（归并）排序

2.3.1 解题思想

归并排序使用了一种分治思想，分治思想的意思就是’分而治之"，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单地直接求解。

即先将无序序列划分为有序子序列，再将有序子序列合并成一个有序序列的有效的排序算法。

下图会帮助更好的理解：

2.3.2 c++代码

#include <iostream>
#include <vector>

using namespace std;
void Merge(vector<int> vec, int left, int right, int mid)
{
  int i = left, j = mid + 1, k = 0;
  vector<int> temp; //used to save sorted elements.

  while( i <= mid && j < right)
    {
      if(vec[i] < vec[j]) temp[k++] = vec[i++];
      else
        temp[k++] = vec[j++];
    }

  while( j<=right )
    {
      temp[k++] = vec[j++];
    }
  while(i< left)
    {
      temp[k++] = vec[i++];
    }
  for(int i = left, j= 0; i <= right; i++, j++)
    {
      vec[i] = temp[j];
    }
}

void MergeSort(vector<int> vec, int left, int right )
{
  if(left > right) return;

  int mid = (left + right) / 2;

  MergeSort(vec, left, mid);
  MergeSort(vec, mid + 1, right);
  Merge(vec,left, right, mid );
}

int main()
{
  vector<int> s = {5,4,6,31};
  MergeSort(s,0,s.size()-1);
  for (int i = 0; i < s.size(); i ++ ) cout << s[i] << ' ' ;
  cout << endl;

  return 0;
}

2.4 快速排序

2.4.1 基本思想

选取待排序组合A的某个元素t=A[s]，然后将其他元素重新排列，使A[0…n-1]中所有在t以前出现的元素都小于或等于t，而在t之后出现的元素都大于或等于t。

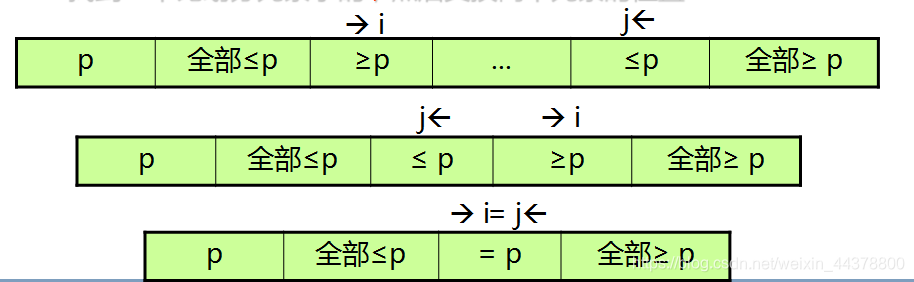
说白了就是选择一个基准，是的基准左边的都比基准小，基准右边的都比基准大，如下图所示：

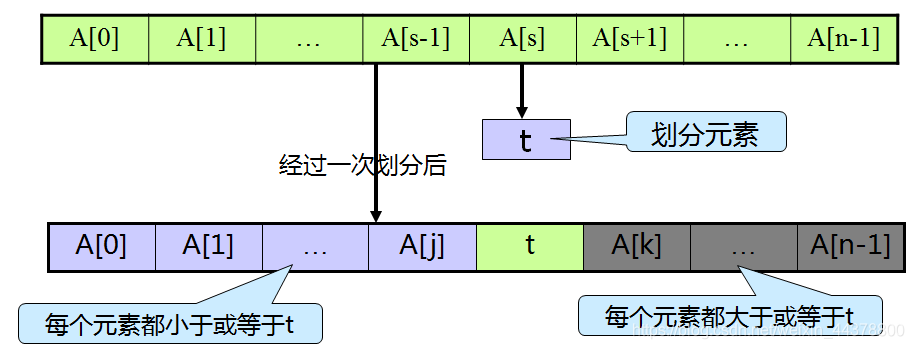
• 快速排序是对于冒泡排序的一种改进；
• 然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列.
• 同时从左、右开始扫描，左边找到一个比划分元素Pivot大的，右边找到一个比划分元素小的，然后交换两个元素的位置。

2.4.2 c++代码