插入排序算法详解-CSDN博客

本文深入解析插入排序算法的特性，包括其确定性、可行性及有穷性。通过伪代码展示算法流程，阐述正确的算法应如何在任意输入下得到正确输出，并详细解释循环不变量的概念及其在插入排序中的应用。

算法

算法的特点

Input,output(输入，输出)
Deterministic(确定性)
Feasible(可行性）
Finite(有穷性)

算法的描述

Psudocode(伪代码)
在这里插入图片描述

插入排序：
InserSort(A)
for j←2 to n do//我拿上来的牌就是J
	key←A[j]
	i←j-1//i表示牌的位置
	while i>0 and A[i]>key do
		A[i+1]←A[i]
		i←i-1
	A[i+1]←key
return A

算法的正确性

正确的算法
对任意一个输入，算法能得到一个正确的输出
循环不变量
与程序变量有关的一个语句，它在循环刚开始前，以及在循环的每个迭代执行后为真，特别是在循环结束后，仍然为真。
插入排序的循环不变量
在for循环第j个迭代执行前，子数组A[1```j-1]由最初A[1````j-1]中的元素构成，不过现在是有序的。

我们任何一个算法其实就是一个迭代算法
循环算法和迭代算法其实都是一样的
这个循环变量如何找到？就是最难的地方
在插入排序算法中
for()
在执行第K部的时候，我们前面的A[1]---A[k-1]，比如我们排序的目标是由小到大，这些元素保存的就是a[1]---a[k-1]的元素

在这里插入图片描述
我们要找一个最大的数
max=A[i]

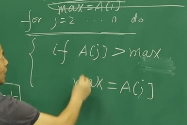
在我们执行j=k之前，前面的max一定是前面k-1个元素中最大的
当j=n+1时，循环就跳出来了，出来的结果就是前面n个元素中最大的
所以这个就是循环不变量，在循环结束之前都为真

我们来证明一下：
在这里插入图片描述

在排序算法中，我们的循环不变量可以被作为Lj-1

在这里插入图片描述
插入算法的证明

循环不变量： j=k
Lk-1 A[I]到A[K-1]是有序的
初始步，j=2
L1: A[1]
LK-1 A[I]----A[k-1]
从小到大
在这里插入图片描述
要验证LK对不对

A[k]=k时，要完成这个迭代

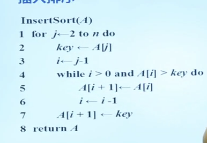
while循环里面要进行插入，
一定要按照算法来执行

当k=n+1时，循环退出