LeetCode刷题指南 - 动态规划篇

以下内容学习labuladong 的算法笔记时，所做的笔记记录，仅供学习使用感谢。

一、动态规划基本技巧

① 动态规划解题框架

注意：

1、动态规划问题的一般形式就是求最值。

2、存在「重叠子问题」，需要「备忘录」或者「DP table」来优化穷举过程

**3、求解动态规划的核心问题是穷举，通过列出正确的「状态转移方程」：明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case **

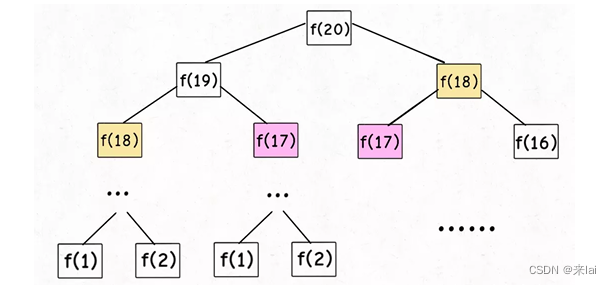
509、斐波那契数列问题

1、暴力递归

int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

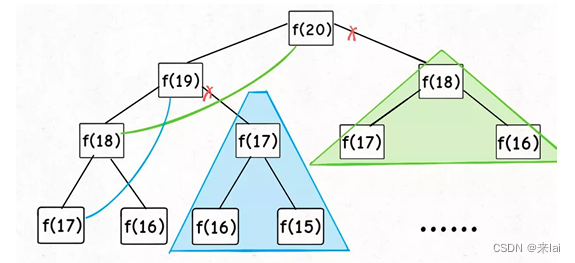
2、带备忘录的递归解法

int fib(int N) {
    if (N < 1) return 0;
    // 备忘录全初始化为 0
   int[] memo= new int[n+1];
    // 初始化最简情况
    return helper(memo, N);
}

int helper(int[] memo, int n) {
    // base case 
    if (n == 1 || n == 2) return 1;
    // 已经计算过
    if (memo[n] != 0) return memo[n];
    memo[n] = helper(memo, n - 1) + 
                helper(memo, n - 2);
    return memo[n];
}

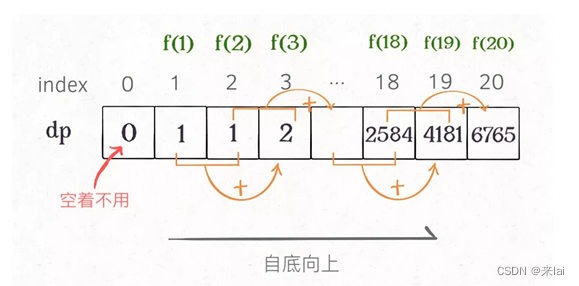
3、dp 数组的迭代解法

int fib(int N) {
    int dp[] = new int[31];
    // base case
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];
}

//优化空间，因为只用记录前两个记录就可以
int fib(int n) {
    if (n == 2 || n == 1) 
        return 1;
    int prev = 1, curr = 1;
    for (int i = 3; i <= n; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

322、零钱兑换问题

1、暴力递归(会超时)

//纯递归，超时
public int coinChange(int[] coins, int amount) {
    return result(coins,amount,0);
}
//减少数组下标为i的硬币值后，子问题的最优解，最终答案为子问题最优解+1
public int result(int[] coins,int amount,int index){
    if(amount==0)  return 0;
    if(amount<0)  return -1;
    int min = Integer.MAX_VALUE; //amount减少一个硬币后，硬币个数最少（最优解为min+1）
    for(int i = 0;i<coins.length;i++){
        int cur = result(coins, amount-coins[i],i);//递归求依次减少值为coin[i]的硬币后，每个子问题的最优解
        //如果值为-1，暂时先不考虑
        if(cur==-1){
            continue;
        }
        //求当前所有子问题最优解中，需要硬币个数最少的
        if(cur < min ){
            min = cur;
        }
    }
    //如果此时，最小值仍为初始值，证明当前问题无最优解，返回-1
    if(min == Integer.MAX_VALUE){
        return -1;
    }else{ //否则，返回子问题中，硬币最少的最优解
        return min+1;
    }
}

以上代码的数学形式就是状态转移方程：

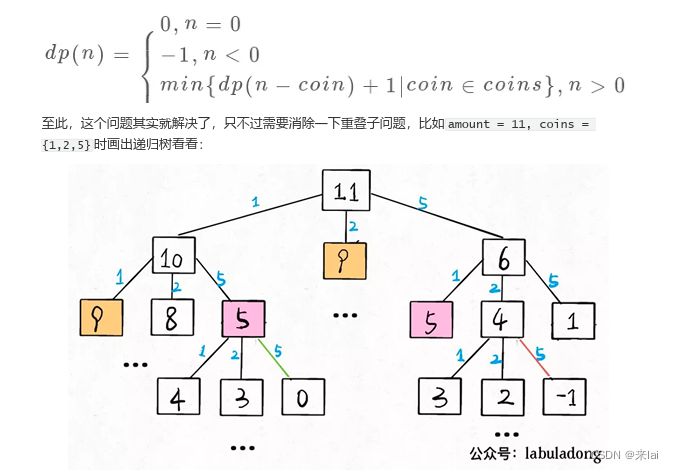
时间复杂度分析：子问题总数 x 解决每个子问题的时间。

子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(k * n^k)，指数级别。

2、带备忘录的递归

public int coinChange(int[] coins, int amount) {
    //面值<1时，需要0个硬币
    if(amount<1)  return 0;
    return result(coins,amount, new int[amount+1]);
}
public int result(int[] coins,int amount,int[] memo){ //memo[]备忘录
    //总数为0，返回0个硬币
    if(amount==0)  return 0;
    if(amount<0)  return -1;
    if(memo[amount]!=0)  return memo[amount];//如果备忘录中有当前值，找到它
    int min = Integer.MAX_VALUE; //amount减少一个硬币后，硬币个数最少（最优解）
    for(int i = 0;i<coins.length;i++){
        int cur = result(coins, amount-coins[i],memo);//子问题
        if(cur==-1){
            continue;
        }
        if(cur < min&&cur>=0){
            min = cur;
        }
    }
    if(min== Integer.MAX_VALUE){
        return memo[amount]=-1;
    }else{
        memo[amount]=min+1;
    }
    return memo[amount];
}

很显然「备忘录」大大减小了子问题数目，完全消除了子问题的冗余，所以子问题总数不会超过金额数 n，即子问题数目为 O(n)。处理一个子问题的时间不变，仍是 O(k)，所以总的时间复杂度是 O(kn)。

3、dp 数组的迭代解法

//自底向上迭代解法
//动态规划迭代 dp[i] = x表示，当目标金额为i时，至少需要x枚硬币。
public int coinChange(int[] coins, int amount) {
    //dp[i]表示，当目标金额为i时，至少需要dp[i]枚硬币凑出
    int[] dp = new int[amount + 1];//范围0-amount
    //dp数组全部初始化为特殊值 amount+1
    Arrays.fill(dp, amount + 1);//dp[]={amount+1,amount+1,amount+1,amount+1...}
    //base case
    dp[0]=0;
    //遍历所有状态amount
    for(int i=1;i<= amount;i++){
        //遍历所有面额的硬币
        for(int coin:coins){
            //子问题无解跳过
            if(i-coin < 0 ){
                continue;
            }
            //状态转移
            dp[i]=Math.min(dp[i],dp[i-coin]+1);
        }
    }
    //看看金额amount是否可以凑出来，dp[0]==0+1,就取值-1
    return (dp[amount] == amount + 1) ? -1 : dp[amount];
}

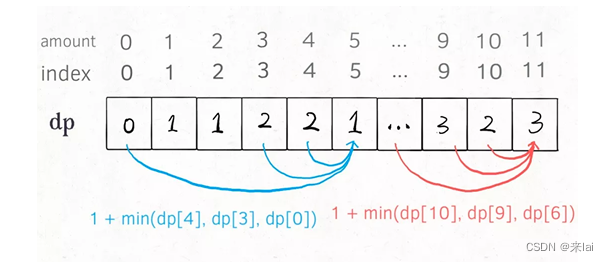
PS：为啥dp数组初始化为amount + 1呢，因为凑成amount金额的硬币数最多只可能等于amount（全用 1 元面值的硬币），所以初始化为amount + 1就相当于初始化为正无穷，便于后续取最小值。

② 动态规划答疑篇

一、最优子结构详解

**「最优子结构」**是某些问题的一种特定性质，并不是动态规划问题专有的。也就是说，很多问题其实都具有最优子结构，只是其中大部分不具有重叠子问题，所以我们不把它们归为动态规划系列问题而已。

我先举个很容易理解的例子：假设你们学校有 10 个班，你已经计算出了每个班的最高考试成绩。那么现在我要求你计算全校最高的成绩，你会不会算？当然会，而且你不用重新遍历全校学生的分数进行比较，而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩。

我给你提出的这个问题就符合最优子结构：可以从子问题的最优结果推出更大规模问题的最优结果。让你算每个班的最优成绩就是子问题，你知道所有子问题的答案后，就可以借此推出全校学生的最优成绩这个规模更大的问题的答案。

你看，这么简单的问题都有最优子结构性质，只是因为显然没有重叠子问题，所以我们简单地求最值肯定用不出动态规划。

再举个例子：假设你们学校有 10 个班，你已知每个班的最大分数差（最高分和最低分的差值）。那么现在我让你计算全校学生中的最大分数差，你会不会算？可以想办法算，但是肯定不能通过已知的这 10 个班的最大分数差推到出来。因为这 10 个班的最大分数差不一定就包含全校学生的最大分数差，比如全校的最大分数差可能是 3 班的最高分和 6 班的最低分之差。

这次我给你提出的问题就不符合最优子结构，因为你没办通过每个班的最优值推出全校的最优值，没办法通过子问题的最优值推出规模更大的问题的最优值。前文 动态规划详解 说过，想满足最优子结，子问题之间必须互相独立。全校的最大分数差可能出现在两个班之间，显然子问题不独立，所以这个问题本身不符合最优子结构。

那么遇到这种最优子结构失效情况，怎么办？策略是：改造问题。对于最大分数差这个问题，我们不是没办法利用已知的每个班的分数差吗，那我只能这样写一段暴力代码：

int result = 0;
for (Student a : school) {
    for (Student b : school) {
        if (a is b) continue;
        result = max(result, |a.score - b.score|);
    }
}
return result;

改造问题，也就是把问题等价转化：最大分数差，不就等价于最高分数和最低分数的差么，那不就是要求最高和最低分数么，不就是我们讨论的第一个问题么，不就具有最优子结构了么？那现在改变思路，借助最优子结构解决最值问题，再回过头解决最大分数差问题，是不是就高效多了？

当然，上面这个例子太简单了，不过请读者回顾一下，我们做动态规划问题，是不是一直在求各种最值，本质跟我们举的例子没啥区别，无非需要处理一下重叠子问题。

前文 动态规划：不同的定义产生不同的解法 和 经典动态规划：高楼扔鸡蛋（进阶篇） 就展示了如何改造问题，不同的最优子结构，可能导致不同的解法和效率。

再举个常见但也十分简单的例子，求一棵二叉树的最大值，不难吧（简单起见，假设节点中的值都是非负数）：

int maxVal(TreeNode root) {    
    if (root == null)      
        return -1;    
    int left = maxVal(root.left);   
    int right = maxVal(root.right);   
    return max(root.val, left, right);
}

你看这个问题也符合最优子结构，以root为根的树的最大值，可以通过两边子树（子问题）的最大值推导出来，结合刚才学校和班级的例子，很容易理解吧。

当然这也不是动态规划问题，旨在说明，最优子结构并不是动态规划独有的一种性质，能求最值的问题大部分都具有这个性质；但反过来，最优子结构性质作为动态规划问题的必要条件，一定是让你求最值的，以后碰到那种恶心人的最值题，思路往动态规划想就对了，这就是套路。

动态规划不就是从最简单的 base case 往后推导吗，可以想象成一个链式反应，不断以小博大。但只有符合最优子结构的问题，才有发生这种链式反应的性质。

找最优子结构的过程，其实就是证明状态转移方程正确性的过程，方程符合最优子结构就可以写暴力解了，写出暴力解就可以看出有没有重叠子问题了，有则优化，无则 OK。这也是套路，经常刷题的朋友应该能体会。

这里就不举那些正宗动态规划的例子了，读者可以翻翻历史文章，看看状态转移是如何遵循最优子结构的，这个话题就聊到这，下面再来看另外个动态规划迷惑行为。

二、dp 数组的遍历方向

我相信读者做动态规划问题时，肯定会对dp数组的遍历顺序有些头疼。我们拿二维dp数组来举例，有时候我们是正向遍历：

int[][] dp = new int[m][n];
for (int i = 0; i < m; i++)
    for (int j = 0; j < n; j++)
        // 计算 dp[i][j]

有时候我们反向遍历：

for (int i = m - 1; i >= 0; i--)
    for (int j = n - 1; j >= 0; j--)
        // 计算 dp[i][j]

有时候可能会斜向遍历：

// 斜着遍历数组
for (int l = 2; l <= n; l++) {
    for (int i = 0; i <= n - l; i++) {
        int j = l + i - 1;
        // 计算 dp[i][j]
    }
}

甚至更让人迷惑的是，有时候发现正向反向遍历都可以得到正确答案，比如我们在 团灭 LeetCode 股票买卖问题 中有的地方就正反皆可。

那么，如果仔细观察的话可以发现其中的原因的。你只要把住两点就行了：

1、遍历的过程中，所需的状态必须是已经计算出来的。

2、遍历的终点必须是存储结果的那个位置。

下面来具体解释上面两个原则是什么意思。

比如编辑距离这个经典的问题，详解见前文 经典动态规划：编辑距离，我们通过对dp数组的定义，确定了 base case 是dp[..][0]和dp[0][..]，最终答案是dp[m][n]；而且我们通过状态转移方程知道dp[i][j]需要从dp[i-1][j],dp[i][j-1],dp[i-1][j-1]转移而来，如下图：

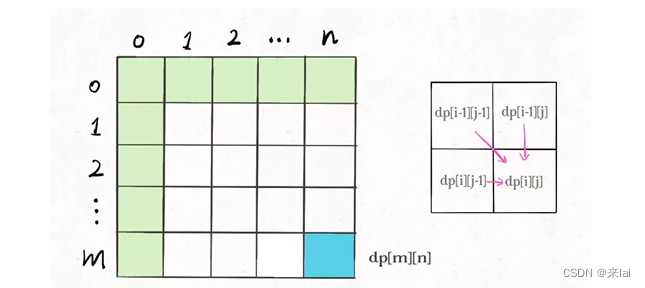
那么，参考刚才说的两条原则，你该怎么遍历dp数组？肯定是正向遍历：

for (int i = 1; i < m; i++)
    for (int j = 1; j < n; j++)
        // 通过 dp[i-1][j], dp[i][j - 1], dp[i-1][j-1]
        // 计算 dp[i][j]

因为，这样每一步迭代的左边、上边、左上边的位置都是 base case 或者之前计算过的，而且最终结束在我们想要的答案dp[m][n]。

再举一例，回文子序列问题，详见前文 子序列解题模板：最长回文子序列，我们通过过对dp数组的定义，确定了 base case 处在中间的对角线，dp[i][j]需要从dp[i+1][j],dp[i][j-1],dp[i+1][j-1]转移而来，想要求的最终答案是dp[0][n-1]，如下图：

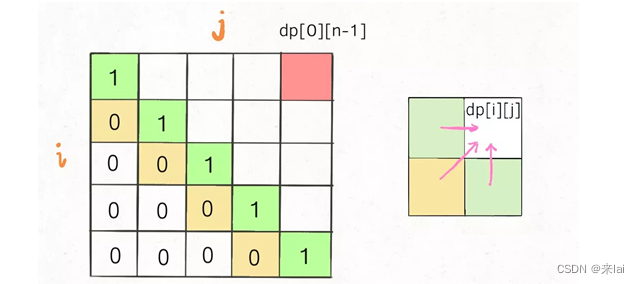
这种情况根据刚才的两个原则，就可以有两种正确的遍历方式：

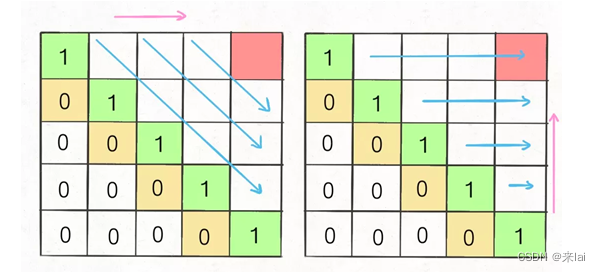
要么从左至右斜着遍历，要么从下向上从左到右遍历，这样才能保证每次dp[i][j]的左边、下边、左下边已经计算完毕，最终得到正确结果。

现在，你应该理解了这两个原则，主要就是看 base case 和最终结果的存储位置，保证遍历过程中使用的数据都是计算完毕的就行，有时候确实存在多种方法可以得到正确答案，可根据个人口味自行选择。

③ base case 和备忘录怎么定

931.下降路径最小和

看下力扣第 931 题「下降路径最小和」，输入为一个n * n的二维数组matrix，请你计算从第一行落到最后一行，经过的路径和最小为多少。

函数签名如下：

int minFallingPathSum(int[][] matrix);

就是说你可以站在matrix的第一行的任意一个元素，需要下降到最后一行。

每次下降，可以向下、向左下、向右下三个方向移动一格。也就是说，可以从matrix[i][j]降到matrix[i+1][j]或matrix[i+1][j-1]或matrix[i+1][j+1]三个位置。

请你计算下降的「最小路径和」，比如说题目给了一个例子：

我们前文写过两道「路径和」相关的文章：动态规划之最小路径和 和 用动态规划算法通关魔塔。

今天这道题也是类似的，不算是困难的题目，所以我们借这道题来讲讲 base case 的返回值、备忘录的初始值、索引越界情况的返回值如何确定。

不过还是要通过 动态规划的标准套路 介绍一下这道题的解题思路，首先我们可以定义一个dp数组：

int dp(int[][] matrix, int i, int j);

这个dp函数的含义如下：

从第一行（matrix[0][..]）向下落，落到位置matrix[i][j]的最小路径和为dp(matrix, i, j)。

根据这个定义，我们可以把主函数的逻辑写出来：

public int minFallingPathSum(int[][] matrix) {
    int n = matrix.length;
    int res = Integer.MAX_VALUE;

    // 终点可能在最后一行的任意一列
    for (int j = 0; j < n; j++) {
        res = Math.min(res, dp(matrix, n - 1, j));
    }

    return res;
}

因为我们可能落到最后一行的任意一列，所以要穷举一下，看看落到哪一列才能得到最小的路径和。

接下来看看dp函数如何实现。

对于matrix[i][j]，只有可能从matrix[i-1][j], matrix[i-1][j-1], matrix[i-1][j+1]这三个位置转移过来。

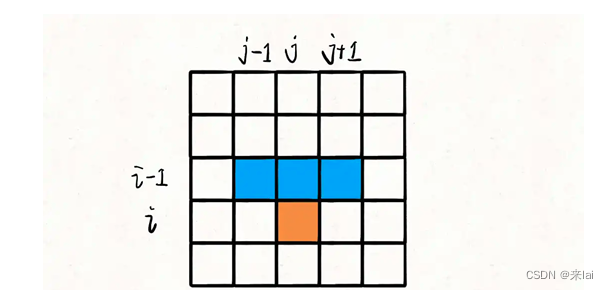
那么，只要知道到达(i-1, j), (i-1, j-1), (i-1, j+1)这三个位置的最小路径和，加上matrix[i][j]的值，就能够计算出来到达位置(i, j)的最小路径和：

//暴力法
int dp(int[][] matrix, int i, int j) {
    // 非法索引检查
    if (i < 0 || j < 0 ||
        i >= matrix.length ||
        j >= matrix[0].length) {
        // 返回一个特殊值
        return 99999;
    }
    // base case
    if (i == 0) {
        return matrix[i][j];
    }
    // 状态转移
    return matrix[i][j] + min(
            dp(matrix, i - 1, j), 
            dp(matrix, i - 1, j - 1),
            dp(matrix, i - 1, j + 1)
        );
}
int min(int a, int b, int c) {
    return Math.min(a, Math.min(b, c));
}

当然，上述代码是暴力穷举解法，我们可以用备忘录的方法消除重叠子问题，完整代码如下：

//备忘录法
public int minFallingPathSum(int[][] matrix) {
    int n = matrix.length;
    int res = Integer.MAX_VALUE;
    // 备忘录里的值初始化为 66666
    memo = new int[n][n];
    for (int i = 0; i < n; i++) {
        Arrays.fill(memo[i], 66666);
    }
    // 终点可能在 matrix[n-1] 的任意一列
    for (int j = 0; j < n; j++) {
        res = Math.min(res, dp(matrix, n - 1, j));
    }
    return res;
}
int[][] memo;// 备忘录
int dp(int[][] matrix, int i, int j) {
    // 1、索引合法性检查
    if (i < 0 || j < 0 ||
        i >= matrix.length ||
        j >= matrix[0].length) {

        return 99999;
    }
    // 2、base case
    if (i == 0) {
        return matrix[0][j];
    }
    // 3、查找备忘录，防止重复计算
    if (memo[i][j] != 66666) {
        return memo[i][j];
    }
    // 进行状态转移
    memo[i][j] = matrix[i][j] + min(
            dp(matrix, i - 1, j), 
            dp(matrix, i - 1, j - 1),
            dp(matrix, i - 1, j + 1)
        );

    return memo[i][j];
}
int min(int a, int b, int c) {
    return Math.min(a, Math.min(b, c));
}

如果看过我们公众号之前的动态规划系列文章，这个解题思路应该是非常容易理解的。

那么本文对于这个dp函数仔细探讨三个问题：

1、对于索引的合法性检测，返回值为什么是 99999？其他的值行不行？

2、base case 为什么是i == 0？

3、备忘录memo的初始值为什么是 66666？其他值行不行？

首先，说说 base case 为什么是i == 0，返回值为什么是matrix[0][j]，这是根据dp函数的定义所决定的。

回顾我们的dp函数定义：

从第一行（matrix[0][..]）向下落，落到位置matrix[i][j]的最小路径和为dp(matrix, i, j)。

根据这个定义，我们就是从matrix[0][j]开始下落。那如果我们想落到的目的地就是i == 0，所需的路径和当然就是matrix[0][j]呗。

再说说备忘录memo的初始值为什么是 66666，这是由题目给出的数据范围决定的。

备忘录memo数组的作用是什么？

就是防止重复计算，将dp(matrix, i, j)的计算结果存进memo[i][j]，遇到重复计算可以直接返回。

那么，我们必须要知道memo[i][j]到底存储计算结果没有，对吧？如果存结果了，就直接返回；没存，就去递归计算。

所以，memo的初始值一定得是特殊值，和合法的答案有所区分。

我们回过头看看题目给出的数据范围：

matrix是n * n的二维数组，其中1 <= n <= 100；对于二维数组中的元素，有-100 <= matrix[i][j] <= 100。

假设matrix的大小是 100 x 100，所有元素都是 100，那么从第一行往下落，得到的路径和就是 100 x 100 = 10000，也就是最大的合法答案。

类似的，依然假设matrix的大小是 100 x 100，所有元素是 -100，那么从第一行往下落，就得到了最小的合法答案 -100 x 100 = -10000。

也就是说，这个问题的合法结果会落在区间[-10000, 10000]中。

所以，我们memo的初始值就要避开区间[-10000, 10000]，换句话说，memo的初始值只要在区间(-inf, -10001] U [10001, +inf)中就可以。

最后，说说对于不合法的索引，返回值应该如何确定，这需要根据我们状态转移方程的逻辑确定。

对于这道题，状态转移的基本逻辑如下：

int dp(int[][] matrix, int i, int j) {

    return matrix[i][j] + min(
            dp(matrix, i - 1, j), 
            dp(matrix, i - 1, j - 1),
            dp(matrix, i - 1, j + 1)
        );
}

显然，i - 1, j - 1, j + 1这几个运算可能会造成索引越界，对于索引越界的dp函数，应该返回一个不可能被取到的值。

因为我们调用的是min函数，最终返回的值是最小值，所以对于不合法的索引，只要dp函数返回一个永远不会被取到的最大值即可。

刚才说了，合法答案的区间是[-10000, 10000]，所以我们的返回值只要大于 10000 就相当于一个永不会取到的最大值。

换句话说，只要返回区间[10001, +inf)中的一个值，就能保证不会被取到。

至此，我们就把动态规划相关的三个细节问题举例说明了。

拓展延伸一下，建议大家做题时，除了题意本身，一定不要忽视题目给定的其他信息。

本文举的例子，测试用例数据范围可以确定「什么是特殊值」，从而帮助我们将思路转化成代码。

除此之外，数据范围还可以帮我们估算算法的时间/空间复杂度。

比如说，有的算法题，你只想到一个暴力求解思路，时间复杂度比较高。如果发现题目给定的数据量比较大，那么肯定可以说明这个求解思路有问题或者存在优化的空间。

除了数据范围，有时候题目还会限制我们算法的时间复杂度，这种信息其实也暗示着一些东西。

比如要求我们的算法复杂度是O(NlogN)，你想想怎么才能搞出一个对数级别的复杂度呢？

肯定得用到 二分搜索 或者二叉树相关的数据结构，比如TreeMap，PriorityQueue之类的对吧。

再比如，有时候题目要求你的算法时间复杂度是O(MN)，这可以联想到什么？

可以大胆猜测，常规解法是用 回溯算法 暴力穷举，但是更好的解法是动态规划，而且是一个二维动态规划，需要一个M * N的二维dp数组，所以产生了这样一个时间复杂度。

dp自底向上解法：

class Solution {
    public  int minFallingPathSum(int[][] matrix) {
        int n=matrix.length;
        if(n==1) return matrix[0][0];//只有一行情况
        int[][] dp=new int[n][n];//// 定义 dp[i][j] 的值为 matrix[i][j] 下降路径的最小值。
        for(int j=0;j<n;j++) {
            dp[0][j]=matrix[0][j];
        }
        for(int i=1;i<n;i++){
            for( int j=0;j<n;j++){
                if(j==0){
                    dp[i][j]=matrix[i][j]+Math.min(dp[i-1][j],dp[i-1][j+1]);
                }else if(j==n-1) {
                    dp[i][j]=matrix[i][j]+Math.min(dp[i-1][j-1],dp[i-1][j]);
                }else{
                    dp[i][j]=matrix[i][j]+Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1]);
                } 
            }
        }
        int res=Integer.MAX_VALUE;
        for(int j=0;j<n;j++){
            res=Math.min(dp[n-1][j],res);
        }
        return res;
    }
}

④ 状态压缩：对动态规划进行降维打击

「状态压缩」技巧，就能够把很多动态规划解法的空间复杂度进一步降低，由 O(N^2) 降低到 O(N)，

能够使用状态压缩技巧的动态规划都是二维dp问题，你看它的状态转移方程，如果计算状态dp[i][j]需要的都是dp[i][j]相邻的状态，那么就可以使用状态压缩技巧，将二维的dp数组转化成一维，将空间复杂度从 O(N^2) 降低到 O(N)。

什么叫「和dp[i][j]相邻的状态」呢，比如前文 最长回文子序列 中，最终的代码如下：

516、最长回文子序列

public int longestPalindromeSubseq(String s) {
    int n = s.length();
    // dp 数组全部初始化为 0
    int dp[][] =new int[n][n];
    for(int[] row:dp){
        Arrays.fill(row,0);
    }
    // base case
    for (int i = 0; i < n; i++)
        dp[i][i] = 1;
    // 反着遍历保证正确的状态转移
    for (int i = n - 2; i >= 0; i--) { //n-2可以看图得出
        for (int j = i + 1; j < n; j++) {
            // 状态转移方程
            if (s.charAt(i) == s.charAt(j))
                dp[i][j] = dp[i + 1][j - 1] + 2;
            else
                dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
    // 整个 s 的最长回文子串长度
    return dp[0][n - 1];
}

PS：我们本文不探讨如何推状态转移方程，只探讨对二维 DP 问题进行状态压缩的技巧。技巧都是通用的，所以如果你没看过前文，不明白这段代码的逻辑也无妨，完全不会阻碍你学会状态压缩。

你看我们对dp[i][j]的更新，其实只依赖于dp[i+1][j-1], dp[i][j-1], dp[i+1][j]这三个状态：

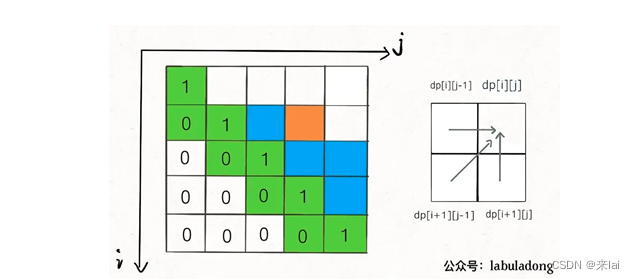
这就叫和dp[i][j]相邻，反正你计算dp[i][j]只需要这三个相邻状态，其实根本不需要那么大一个二维的 dp table 对不对？

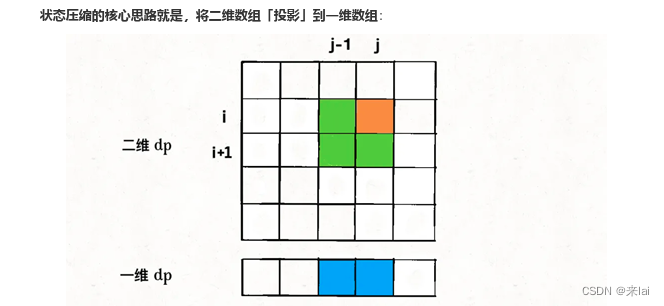
思路很直观，但是也有一个明显的问题，图中dp[i][j-1]和dp[i+1][j-1]这两个状态处在同一列，而一维数组中只能容下一个，那么当我计算dp[i][j]时，他俩必然有一个会被另一个覆盖掉，怎么办？

这就是状态压缩的难点，下面就来分析解决这个问题，还是拿「最长回文子序列」问题举例，它的状态转移方程主要逻辑就是如下这段代码：

for (int i = n - 2; i >= 0; i--) {
    for (int j = i + 1; j < n; j++) {
        // 状态转移方程
        if (s.charAt(i) == s.charAt(j))
            dp[i][j] = dp[i + 1][j - 1] + 2;
        else
            dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
    }
}

想把二维dp数组压缩成一维，一般来说是把第一个维度，也就是i这个维度去掉，只剩下j这个维度。压缩后的一维dp数组就是之前二维dp数组的dp[i][..]那一行。

我们先将上述代码进行改造，直接无脑去掉i这个维度，把dp数组变成一维：

for (int i = n - 2; i >= 0; i--) {
    for (int j = i + 1; j < n; j++) {
        // 在这里，一维 dp 数组中的数是什么？
        if (s.charAt(i) == s.charAt(j))
            dp[j] = dp[j - 1] + 2;
        else
            dp[j] = Math.max(dp[j], dp[j - 1]);
    }
}

上述代码的一维dp数组只能表示二维dp数组的一行dp[i][..]，那我怎么才能得到dp[i+1][j-1], dp[i][j-1], dp[i+1][j]这几个必要的的值，进行状态转移呢？

在代码中注释的位置，将要进行状态转移，更新dp[j]，那么我们要来思考两个问题：

1、在对dp[j]赋新值之前，dp[j]对应着二维dp数组中的什么位置？

2、dp[j-1]对应着二维dp数组中的什么位置？

对于问题 1，在对dp[j]赋新值之前，dp[j]的值就是外层 for 循环上一次迭代算出来的值，也就是对应二维dp数组中dp[i+1][j]的位置。

对于问题 2，dp[j-1]的值就是内层 for 循环上一次迭代算出来的值，也就是对应二维dp数组中dp[i][j-1]的位置。

那么问题已经解决了一大半了，只剩下二维dp数组中的dp[i+1][j-1]这个状态我们不能直接从一维dp数组中得到：

for (int i = n - 2; i >= 0; i--) {
    for (int j = i + 1; j < n; j++) {
        if (s.charAt(i) == s.charAt(j))
            // dp[i][j] = dp[i+1][j-1] + 2;
            dp[j] = ?? + 2;
        else
            // dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
            dp[j] = Math.max(dp[j], dp[j - 1]);
    }
}

因为 for 循环遍历i和j的顺序为从右向左，从下向上，所以可以发现，在更新一维dp数组的时候，dp[i+1][j-1]会被dp[i][j-1]覆盖掉，图中标出了这四个位置被遍历到的次序：

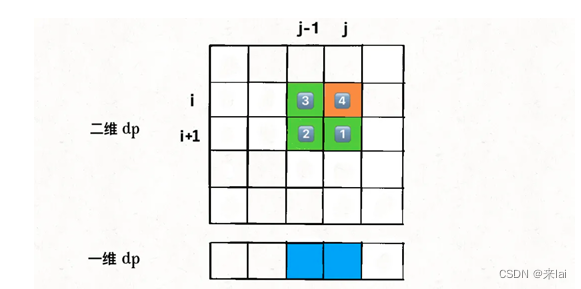
那么如果我们想得到dp[i+1][j-1]，就必须在它被覆盖之前用一个临时变量temp把它存起来，并把这个变量的值保留到计算dp[i][j]的时候。为了达到这个目的，结合上图，我们可以这样写代码：

for (int i = n - 2; i >= 0; i--) {
    // 存储 dp[i+1][j-1] 的变量
    int pre = 0;
    for (int j = i + 1; j < n; j++) {
        int temp = dp[j];
        if (s.charAt(i) == s.charAt(j))
            // dp[i][j] = dp[i+1][j-1] + 2;
            dp[j] = pre + 2;
        else
            dp[j] = Math.max(dp[j], dp[j - 1]);        
        // 到下一轮循环，pre 就是 dp[i+1][j-1] 了
        pre = temp;
    }
}

别小看这段代码，这是一维dp最精妙的地方，会者不难，难者不会。为了清晰起见，我用具体的数值来拆解这个逻辑：

假设现在i = 5, j = 7且s[5] == s[7]，那么现在会进入下面这个逻辑对吧：

if (s.charAt(5) == s.charAt(7))
    // dp[5][7] = dp[i+1][j-1] + 2;
    dp[7] = pre + 2;

我问你这个pre变量是什么？是内层 for 循环上一次迭代的temp值。

那我再问你内层 for 循环上一次迭代的temp值是什么？是dp[j-1]也就是dp[6]，但这是外层 for 循环上一次迭代对应的dp[6]，也就是二维dp数组中的dp[i+1][6] = dp[6][6]。

也就是说，pre变量就是dp[i+1][j-1] = dp[6][6]，也就是我们想要的结果。

那么现在我们成功对状态转移方程进行了降维打击，算是最硬的的骨头啃掉了，但注意到我们还有 base case 要处理呀：

// dp 数组全部初始化为 0
int dp[][] =new int[n][n];
for(int[] row:dp){
    Arrays.fill(row,0);
}
// base case
for (int i = 0; i < n; i++)
    dp[i][i] = 1;

如何把 base case 也打成一维呢？**很简单，记住，状态压缩就是投影，**我们把 base case 投影到一维看看：

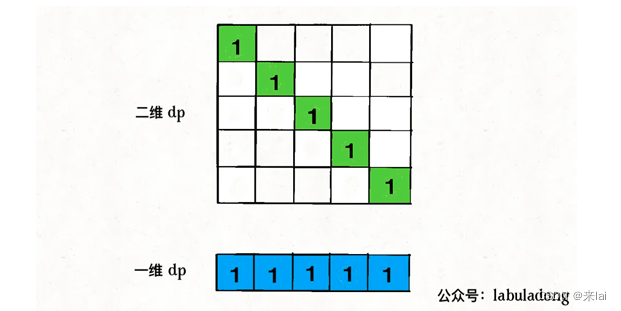
二维dp数组中的 base case 全都落入了一维dp数组，不存在冲突和覆盖，所以说我们直接这样写代码就行了：

// 一维 dp 数组全部初始化为 1
int[] dp =new int[n];
Arrays.fill(dp,1);

至此，我们把 base case 和状态转移方程都进行了降维，实际上已经写出完整代码了：

class Solution {
    int longestPalindromeSubseq(String s) {
        int n = s.length();
        // base case：一维 dp 数组全部初始化为 1
        int[] dp =new int[n];
        Arrays.fill(dp,1);
        for (int i = n - 2; i >= 0; i--) {
            int pre = 0;
            for (int j = i + 1; j < n; j++) {
                int temp = dp[j];
                // 状态转移方程
                if (s.charAt(i) == s.charAt(j))
                    dp[j] = pre + 2;
                else
                    dp[j] = Math.max(dp[j], dp[j - 1]);
                pre = temp;
            }
        }
        return dp[n - 1];
    }
}

本文就结束了，不过状态压缩技巧再牛逼，也是基于常规动态规划思路之上的。

你也看到了，使用状态压缩技巧对二维dp数组进行降维打击之后，解法代码的可读性变得非常差了，如果直接看这种解法，任何人都是一脸懵逼的。

算法的优化就是这么一个过程，先写出可读性很好的暴力递归算法，然后尝试运用动态规划技巧优化重叠子问题，最后尝试用状态压缩技巧优化空间复杂度。

⑤ 动态规划和回溯算法到底谁大？

我们前文经常说回溯算法和递归算法有点类似，有的问题如果实在想不出状态转移方程，尝试用回溯算法暴力解决也是一个聪明的策略，总比写不出来解法强。

那么，回溯算法和动态规划到底是啥关系？它俩都涉及递归，算法模板看起来还挺像的，都涉及做「选择」，真的酷似父与子。

那么，它俩具体有啥区别呢？回溯算法和动态规划之间，是否可能互相转化呢？

今天就用力扣第 494 题「目标和」来详细对比一下回溯算法和动态规划，真可谓群魔乱舞：

494 .目标和

注意，给出的例子 nums 全是 1，但实际上可以是任意正整数哦。

一、回溯思路

其实我第一眼看到这个题目，花了两分钟就写出了一个回溯解法。

任何算法的核心都是穷举，回溯算法就是一个暴力穷举算法，前文 回溯算法解题框架 就写了回溯算法框架：

def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

关键就是搞清楚什么是「选择」，而对于这道题，「选择」不是明摆着的吗？

对于每个数字 nums[i]，我们可以选择给一个正号 + 或者一个负号 -，然后利用回溯模板穷举出来所有可能的结果，数一数到底有几种组合能够凑出 target 不就行了嘛？

伪码思路如下：

def backtrack(nums, i):
    if i == len(nums):
        if 达到 target:
            result += 1
        return

    for op in { +1, -1 }:
        选择 op * nums[i]
        # 穷举 nums[i + 1] 的选择
        backtrack(nums, i + 1)
        撤销选择

如果看过我们之前的几篇回溯算法文章，这个代码可以说是比较简单的了：

int result = 0;

/* 主函数 */
int findTargetSumWays(int[] nums, int target) {
    if (nums.length == 0) return 0;
    backtrack(nums, 0, target);
    return result;
}

/* 回溯算法模板 */
void backtrack(int[] nums, int i, int rest) {
    // base case
    if (i == nums.length) {
        if (rest == 0) {
            // 说明恰好凑出 target
            result++;
        }
        return;
    }
    // 给 nums[i] 选择 - 号
    rest += nums[i];
    // 穷举 nums[i + 1]
    backtrack(nums, i + 1, rest);
    // 撤销选择
    rest -= nums[i]; 

    // 给 nums[i] 选择 + 号
    rest -= nums[i];
    // 穷举 nums[i + 1]
    backtrack(nums, i + 1, rest);
    // 撤销选择
    rest += nums[i];
}

有的读者可能问，选择 - 的时候，为什么是 rest += nums[i]，选择 + 的时候，为什么是 rest -= nums[i] 呢，是不是写反了？

不是的，「如何凑出 target」和「如何把 target 减到 0」其实是一样的。我们这里选择后者，因为前者必须给 backtrack 函数多加一个参数，我觉得不美观：

void backtrack(int[] nums, int i, int sum, int target) {
    // base case
    if (i == nums.length) {
        if (sum == target) {
            result++;
        }
        return;
    }
    // ...
}

因此，如果我们给 nums[i] 选择 + 号，就要让 rest - nums[i]，反之亦然。

以上回溯算法可以解决这个问题，时间复杂度为 O(2^N)，N 为 nums 的大小。这个复杂度怎么算的？回忆前文 学习数据结构和算法的框架思维，发现这个回溯算法就是个二叉树的遍历问题：

void backtrack(int[] nums, int i, int rest) {
    if (i == nums.length) {
        return;
    }
    backtrack(nums, i + 1, rest - nums[i]);
    backtrack(nums, i + 1, rest + nums[i]);
}

树的高度就是 nums 的长度嘛，所以说时间复杂度就是这棵二叉树的节点数，为 O(2^N)，其实是非常低效的。

那么，这个问题如何用动态规划思想进行优化呢？

二、消除重叠子问题

动态规划之所以比暴力算法快，是因为动态规划技巧消除了重叠子问题。

如何发现重叠子问题？看是否可能出现重复的「状态」。对于递归函数来说，函数参数中会变的参数就是「状态」，对于 backtrack 函数来说，会变的参数为 i 和 rest。

前文 动态规划之编辑距离 说了一种一眼看出重叠子问题的方法，先抽象出递归框架：

void backtrack(int i, int rest) {
    backtrack(i + 1, rest - nums[i]);
    backtrack(i + 1, rest + nums[i]);
}

举个简单的例子，如果 nums[i] = 0，会发生什么？

void backtrack(int i, int rest) {
    backtrack(i + 1, rest);
    backtrack(i + 1, rest);
}

你看，这样就出现了两个「状态」完全相同的递归函数，无疑这样的递归计算就是重复的。这就是重叠子问题，而且只要我们能够找到一个重叠子问题，那一定还存在很多的重叠子问题。

因此，状态 (i, rest) 是可以用备忘录技巧进行优化的：

int findTargetSumWays(int[] nums, int target) {
    if (nums.length == 0) return 0;
    return dp(nums, 0, target);
}

// 备忘录
HashMap<String, Integer> memo = new HashMap<>();
int dp(int[] nums, int i, int rest) {
    // base case
    if (i == nums.length) {
        if (rest == 0) return 1;
        return 0;
    }
    // 把它俩转成字符串才能作为哈希表的键
    String key = i + "," + rest;
    // 避免重复计算
    if (memo.containsKey(key)) {
        return memo.get(key);
    }
    // 还是穷举
    int result = dp(nums, i + 1, rest - nums[i]) + dp(nums, i + 1, rest + nums[i]);
    // 记入备忘录
    memo.put(key, result);
    return result;
}

以前我们都是用 Python 的元组配合哈希表 dict 来做备忘录的，其他语言没有元组，可以用把「状态」转化为字符串作为哈希表的键，这是一个常用的小技巧。

这个解法通过备忘录消除了很多重叠子问题，效率有一定的提升，但是这就结束了吗？

三、动态规划

事情没有这么简单，先来算一算，消除重叠子问题之后，算法的时间复杂度是多少？其实最坏情况下依然是 O(2^N)。

为什么呢？因为我们只不过恰好发现了重叠子问题，顺手用备忘录技巧给优化了，但是底层思路没有变，依然是暴力穷举的回溯算法，依然在遍历一棵二叉树。这只能叫对回溯算法进行了「剪枝」，提升了算法在某些情况下的效率，但算不上质的飞跃。

其实，这个问题可以转化为一个子集划分问题，而子集划分问题又是一个典型的背包问题。动态规划总是这么玄学，让人摸不着头脑……

首先，如果我们把 nums 划分成两个子集 A 和 B，分别代表分配 + 的数和分配 - 的数，那么他们和 target 存在如下关系：

sum(A) - sum(B) = target
sum(A) = target + sum(B)
sum(A) + sum(B) = target + sum(B) + sum(B)
sum(nums) - target = 2 * sum(B)

综上，可以推出 sum(B) = (sum(nums) - target) / 2，也就是把原问题转化成：nums 中存在几个子集 B，使得 B 中元素的和为 (sum(nums) - target) / 2？

类似的子集划分问题我们前文 经典背包问题：子集划分 讲过，现在实现这么一个函数：

/* 计算 nums 中有几个子集的和为 sum */
int subsets(int[] nums, int sum) {}

然后，可以这样调用这个函数：

int findTargetSumWays(int[] nums, int target) {
    int sum = 0;
    for (int n : nums) sum += n;
    // 这两种情况，不可能存在合法的子集划分
    if (sum < target || (sum + target) % 2 == 1) {
        return 0;
    }
    return subsets(nums, (sum - target) / 2); //注意：解决目标和为负数的情况
}

好的，变成背包问题的标准形式：

有一个背包，容量为 sum，现在给你 N 个物品，第 i 个物品的重量为 nums[i - 1]（注意 1 <= i <= N），每个物品只有一个，请问你有几种不同的方法能够恰好装满这个背包？

现在，这就是一个正宗的动态规划问题了，下面按照我们一直强调的动态规划套路走流程：

第一步要明确两点，「状态」和「选择」。

对于背包问题，这个都是一样的，状态就是「背包的容量」和「可选择的物品」，选择就是「装进背包」或者「不装进背包」。

第二步要明确 dp 数组的定义。

按照背包问题的套路，可以给出如下定义：

dp[i][j] = x 表示，若只在前 i 个物品中选择，若当前背包的容量为 j，则最多有 x 种方法可以恰好装满背包。

翻译成我们探讨的子集问题就是，若只在 nums 的前 i 个元素中选择，若目标和为 j，则最多有 x 种方法划分子集。

根据这个定义，显然 dp[0][..] = 0，因为没有物品的话，根本没办法装背包；dp[..][0] = 1，因为如果背包的最大载重为 0，「什么都不装」就是唯一的一种装法。

我们所求的答案就是 dp[N][sum]，即使用所有 N 个物品，有几种方法可以装满容量为 sum 的背包。

第三步，根据「选择」，思考状态转移的逻辑。

回想刚才的 dp 数组含义，可以根据「选择」对 dp[i][j] 得到以下状态转移：

如果不把 nums[i] 算入子集，或者说你不把这第 i 个物品装入背包，那么恰好装满背包的方法数就取决于上一个状态 dp[i-1][j]，继承之前的结果。

如果把 nums[i] 算入子集，或者说你把这第 i 个物品装入了背包，那么只要看前 i - 1 个物品有几种方法可以装满 j - nums[i-1] 的重量就行了，所以取决于状态 dp[i-1][j-nums[i-1]]。

PS：注意我们说的 i 是从 1 开始算的，而数组 nums 的索引时从 0 开始算的，所以 nums[i-1] 代表的是第 i 个物品的重量，j - nums[i-1] 就是背包装入物品 i 之后还剩下的容量。

由于 dp[i][j] 为装满背包的总方法数，所以应该以上两种选择的结果求和，得到状态转移方程：

dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];

然后，根据状态转移方程写出动态规划算法：

/* 计算 nums 中有几个子集的和为 sum */
int subsets(int[] nums, int sum) {
    int n = nums.length;
    int[][] dp = new int[n + 1][sum + 1];
    // base case
    for (int i = 0; i <= n; i++) {
        dp[i][0] = 1;
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= sum; j++) {
            if (j >= nums[i-1]) {
                // 两种选择的结果之和
                dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
            } else {
                // 背包的空间不足，只能选择不装物品 i
                dp[i][j] = dp[i-1][j];
            }
        }
    }
    return dp[n][sum];
}

然后，发现这个 dp[i][j] 只和前一行 dp[i-1][..] 有关，那么肯定可以优化成一维 dp：

/* 计算 nums 中有几个子集的和为 sum */
int subsets(int[] nums, int sum) {
    int n = nums.length;
    int[] dp = new int[sum + 1];
    // base case
    dp[0] = 1;

    for (int i = 1; i <= n; i++) {
        // j 要从后往前遍历
        for (int j = sum; j >= 0; j--) {
            // 状态转移方程
            if (j >= nums[i-1]) {
                dp[j] = dp[j] + dp[j-nums[i-1]];
            } else {
                dp[j] = dp[j];
            }
        }
    }
    return dp[sum];
}

对照二维 dp，只要把 dp 数组的第一个维度全都去掉就行了，唯一的区别就是这里的 j 要从后往前遍历，原因如下：

因为二维压缩到一维的根本原理是，dp[j] 和 dp[j-nums[i-1]] 还没被新结果覆盖的时候，相当于二维 dp 中的 dp[i-1][j] 和 dp[i-1][j-nums[i-1]]。

那么，我们就要做到：在计算新的 dp[j] 的时候，dp[j] 和 dp[j-nums[i-1]] 还是上一轮外层 for 循环的结果。

如果你从前往后遍历一维 dp 数组，dp[j] 显然是没问题的，但是 dp[j-nums[i-1]] 已经不是上一轮外层 for 循环的结果了，这里就会使用错误的状态，当然得不到正确的答案。

现在，这道题算是彻底解决了。

总结一下，回溯算法虽好，但是复杂度高，即便消除一些冗余计算，也只是「剪枝」，没有本质的改进。而动态规划就比较玄学了，经过各种改造，从一个加减法问题变成子集问题，又变成背包问题，经过各种套路写出解法，又搞出状态压缩，还得反向遍历。

现在搞得我都忘了自己是来干嘛的了。嗯，这也许就是动态规划的魅力吧

二、子序列问题

①编辑距离

72.编辑距离

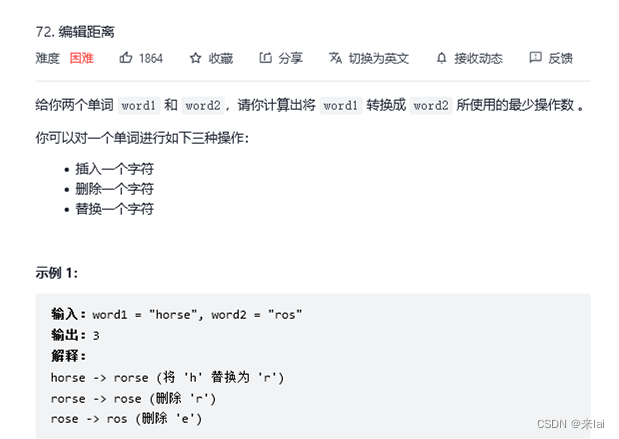
一、思路

编辑距离问题就是给我们两个字符串s1和s2，只能用三种操作，让我们把s1变成s2，求最少的操作数。需要明确的是，不管是把s1变成s2还是反过来，结果都是一样的，所以后文就以s1变成s2举例。

前文 最长公共子序列 说过，解决两个字符串的动态规划问题，一般都是用两个指针i,j分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模。

设两个字符串分别为 “rad” 和 “apple”，为了把s1变成s2，算法会这样进行：

请记住这个 GIF 过程，这样就能算出编辑距离。关键在于如何做出正确的操作，稍后会讲。

根据上面的 GIF，可以发现操作不只有三个，其实还有第四个操作，就是什么都不要做（skip）。比如这个情况：

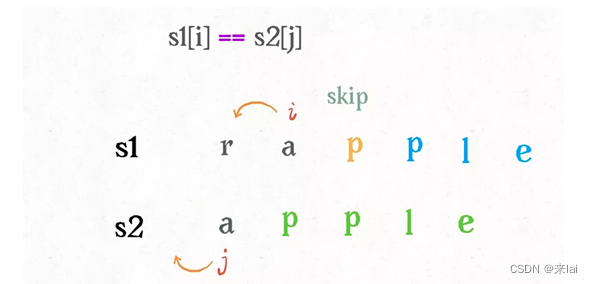
因为这两个字符本来就相同，为了使编辑距离最小，显然不应该对它们有任何操作，直接往前移动i,j即可。

还有一个很容易处理的情况，就是j走完s2时，如果i还没走完s1，那么只能用删除操作把s1缩短为s2。比如这个情况：

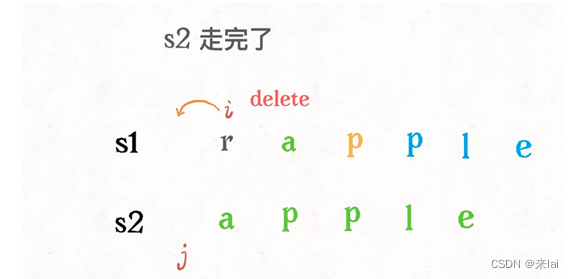
类似的，如果i走完s1时j还没走完了s2，那就只能用插入操作把s2剩下的字符全部插入s1。等会会看到，这两种情况就是算法的 base case。

下面详解一下如何将这个思路转化成代码，坐稳，准备发车了。

二、代码详解

先梳理一下之前的思路：

base case 是i走完s1或j走完s2，可以直接返回另一个字符串剩下的长度。

对于每对儿字符s1[i]和s2[j]，可以有四种操作：

if s1[i] == s2[j]:
    啥都别做（skip）
    i, j 同时向前移动
else:
    三选一：
        插入（insert）
        删除（delete）
        替换（replace）

有这个框架，问题就已经解决了。读者也许会问，这个「三选一」到底该怎么选择呢？很简单，全试一遍，哪个操作最后得到的编辑距离最小，就选谁。这里需要递归技巧，理解需要点技巧，先看下代码：

public int minDistance_1(String s1, String s2) {
    char[] c1 = s1.toCharArray();
    char[] c2 = s2.toCharArray();
    return dp(c1,s1.length() - 1,c2,s2.length() - 1);
}

private int dp(char[] c1, int i, char[] c2, int j) {
    if (i == -1 || j == -1)
        return Math.max(i,j) + 1;
    if (c1[i] == c2[j])
        return dp(c1, i-1, c2, j-1);
    else 
        return 1 + Math.min(
        	Math.min(dp(c1, i - 1, c2, j - 1),  //替换
                     dp(c1, i - 1, c2, j)),     //删除
                     dp(c1, i, c2, j - 1));     //插入
}

下面来详细解释一下这段递归代码，base case 应该不用解释了，主要解释一下递归部分。

都说递归代码的可解释性很好，这是有道理的，只要理解函数的定义，就能很清楚地理解算法的逻辑。我们这里 dp(i, j) 函数的定义是这样的：

def dp(i, j) -> int
# 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离

记住这个定义之后，先来看这段代码：

if s1[i] == s2[j]:
    return dp(i - 1, j - 1)  # 啥都不做
# 解释：
# 本来就相等，不需要任何操作
# s1[0..i] 和 s2[0..j] 的最小编辑距离等于
# s1[0..i-1] 和 s2[0..j-1] 的最小编辑距离
# 也就是说 dp(i, j) 等于 dp(i-1, j-1)

如果s1[i]！=s2[j]，就要对三个操作递归了，稍微需要点思考：

dp(i, j - 1) + 1,    # 插入
# 解释：
# 我直接在 s1[i] 插入一个和 s2[j] 一样的字符
# 那么 s2[j] 就被匹配了，前移 j，继续跟 i 对比
# 别忘了操作数加一

dp(i - 1, j) + 1,    # 删除
# 解释：
# 我直接把 s[i] 这个字符删掉
# 前移 i，继续跟 j 对比
# 操作数加一

dp(i - 1, j - 1) + 1 # 替换
# 解释：
# 我直接把 s1[i] 替换成 s2[j]，这样它俩就匹配了
# 同时前移 i，j 继续对比
# 操作数加一

现在，你应该完全理解这段短小精悍的代码了。还有点小问题就是，这个解法是暴力解法，存在重叠子问题，需要用动态规划技巧来优化。

怎么能一眼看出存在重叠子问题呢？前文 动态规划之正则表达式 有提过，这里再简单提一下，需要抽象出本文算法的递归框架：

def dp(i, j):
    dp(i - 1, j - 1) #1
    dp(i, j - 1)     #2
    dp(i - 1, j)     #3

对于子问题dp(i-1,j-1)，如何通过原问题dp(i,j)得到呢？有不止一条路径，比如dp(i,j)->#1和dp(i,j)->#2->#3。一旦发现一条重复路径，就说明存在巨量重复路径，也就是重叠子问题。

三、动态规划优化

对于重叠子问题呢，前文 动态规划详解 介绍过，优化方法无非是备忘录或者 DP table。

备忘录很好加，原来的代码稍加修改即可：

class Solution {
    /**
     * 备忘录记录重复子问题 自顶向下
     */
    int[][] memo;
    public int minDistance(String s1, String s2) {
        char[] c1 = s1.toCharArray(), c2 = s2.toCharArray();
        memo = new int[c1.length][c2.length];
        return dp(c1, s1.length() - 1, c2, s2.length() - 1);
    }
    //定义：返回s1[0...i]和s2[0....j]的最小编辑距离
    private int dp(char[] c1, int i, char[] c2, int j) {
        //base case
        if (i == -1 || j == -1)
            return Math.max(i,j) + 1;
        //状态转移
        if (c1[i] == c2[j])
            return dp(c1,i - 1,c2,j - 1);
        else {
            if (memo[i][j] != 0)
                return memo[i][j];
            int res = 1 + Math.min(Math.min(dp(c1, i - 1, c2, j - 1), //替换
                                        dp(c1, i - 1, c2, j)), //删除
                               			dp(c1, i, c2, j - 1)); //插入
            memo[i][j] = res;
            return res;
        }
    }
}

主要说下 DP table 的解法：

首先明确 dp 数组的含义，dp 数组是一个二维数组，长这样：

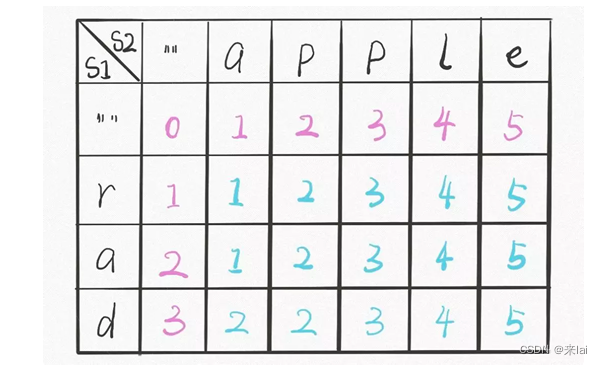
dp[i][j]的含义和之前的 dp 函数类似：

def dp(i, j) -> int
# 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离

dp[i-1][j-1]
# 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离

有了之前递归解法的铺垫，应该很容易理解。dp 函数的 base case 是i,j等于 -1，而数组索引至少是 0，所以 dp 数组会偏移一位，dp[..][0]和dp[0][..]对应 base case。。

既然 dp 数组和递归 dp 函数含义一样，也就可以直接套用之前的思路写代码，唯一不同的是，DP table 是自底向上求解，递归解法是自顶向下求解：

class Solution {
    //自底向上的迭代解法
    public int minDistance(String s1, String s2) {
        int m = s1.length(), n = s2.length();
        int[][] dp = new int[m + 1][n + 1];
        // base case 
        for (int i = 1; i <= m; i++)
            dp[i][0] = i;
        for (int j = 1; j <= n; j++)
            dp[0][j] = j;
        // 自底向上求解
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                if (s1.charAt(i-1) == s2.charAt(j-1))
                    dp[i][j] = dp[i - 1][j - 1];
                else               
                    dp[i][j] = min(
                        dp[i - 1][j] + 1,
                        dp[i][j - 1] + 1,
                        dp[i-1][j-1] + 1
                    );
        // 储存着整个 s1 和 s2 的最小编辑距离
        return dp[m][n];
    }
    int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}

三、扩展延伸

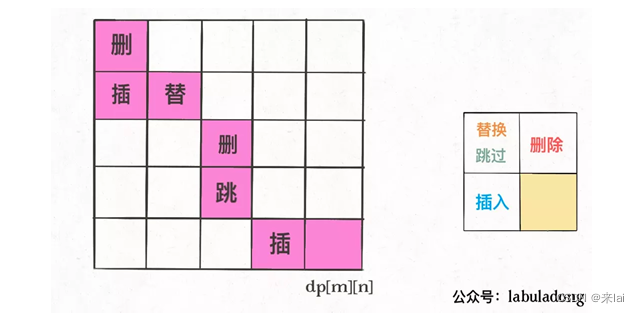
一般来说，处理两个字符串的动态规划问题，都是按本文的思路处理，建立 DP table。为什么呢，因为易于找出状态转移的关系，比如编辑距离的 DP table：

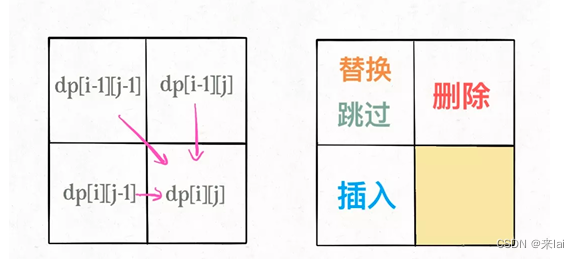
还有一个细节，既然每个dp[i][j]只和它附近的三个状态有关，空间复杂度是可以压缩成 O(min(M,N)) 的（M，N 是两个字符串的长度）。不难，但是可解释性大大降低，读者可以自己尝试优化一下。

你可能还会问，这里只求出了最小的编辑距离，那具体的操作是什么？之前举的修改公众号文章的例子，只有一个最小编辑距离肯定不够，还得知道具体怎么修改才行。

这个其实很简单，代码稍加修改，给 dp 数组增加额外的信息即可：

// int[][] dp;
Node[][] dp;

class Node {
    int val;
    int choice;
    // 0 代表啥都不做
    // 1 代表插入
    // 2 代表删除
    // 3 代表替换
}

val属性就是之前的 dp 数组的数值，choice属性代表操作。在做最优选择时，顺便把操作记录下来，然后就从结果反推具体操作。

我们的最终结果不是dp[m][n]吗，这里的val存着最小编辑距离，choice存着最后一个操作，比如说是插入操作，那么就可以左移一格：

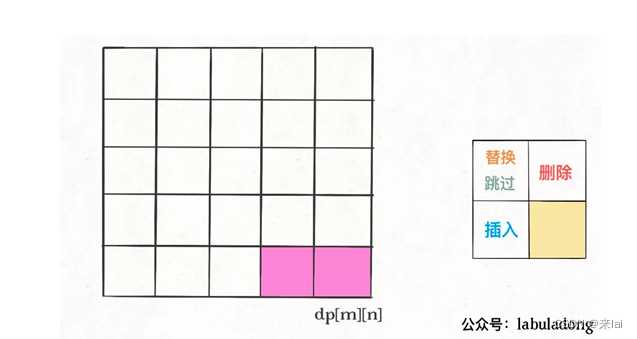
重复此过程，可以一步步回到起点dp[0][0]，形成一条路径，按这条路径上的操作编辑对应索引的字符，就是最佳方案：

②最长递增子序列

300.最长上升子序列

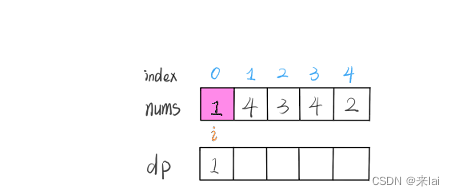
我们的定义是这样的：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。

根据这个定义，我们就可以推出 base case：dp[i] 初始值为 1，因为以 nums[i] 结尾的最长递增子序列起码要包含它自己。

举两个例子：

算法演进的过程是这样的：

根据这个定义，我们的最终结果（子序列的最大长度）应该是 dp 数组中的最大值。

int res = 0;
for (int i = 0; i < dp.size(); i++) {
    res = Math.max(res, dp[i]);
}
return res;

读者也许会问，刚才的算法演进过程中每个 dp[i] 的结果是我们肉眼看出来的，我们应该怎么设计算法逻辑来正确计算每个 dp[i] 呢？

这就是动态规划的重头戏了，要思考如何设计算法逻辑进行状态转移，才能正确运行呢？这里就可以使用数学归纳的思想：

假设我们已经知道了 dp[0..4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢？

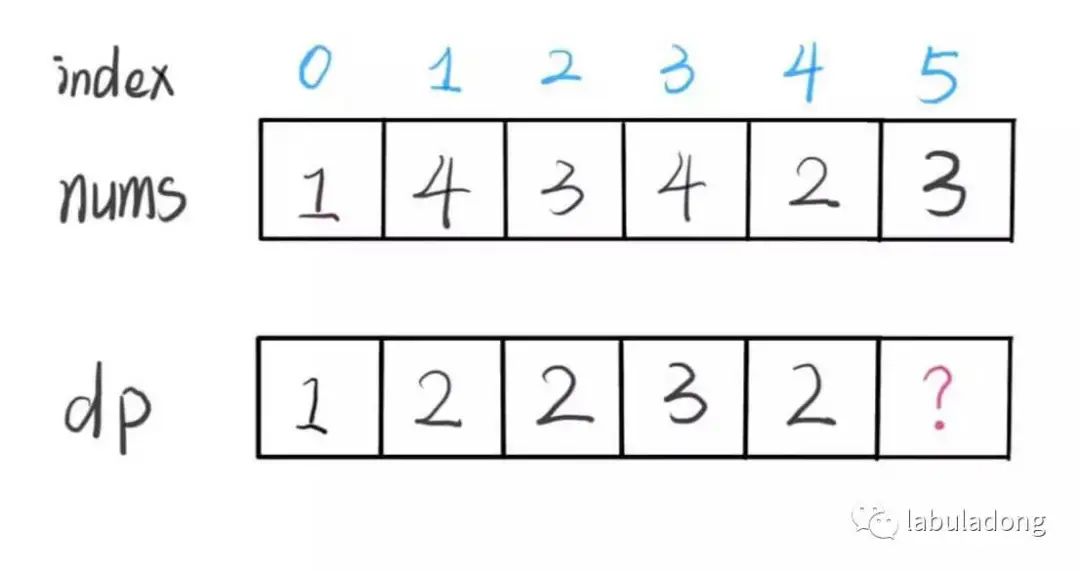
根据刚才我们对 dp 数组的定义，现在想求 dp[5] 的值，也就是想求以 nums[5] 为结尾的最长递增子序列。

nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。

显然，可能形成很多种新的子序列，但是我们只选择最长的那一个，把最长子序列的长度作为 dp[5] 的值即可。

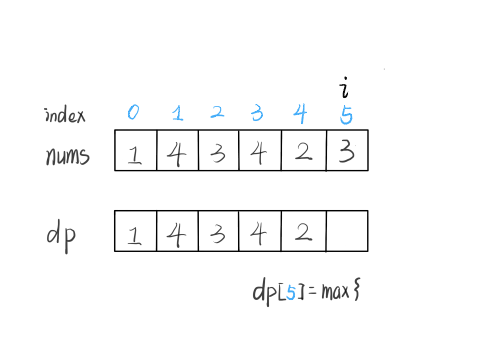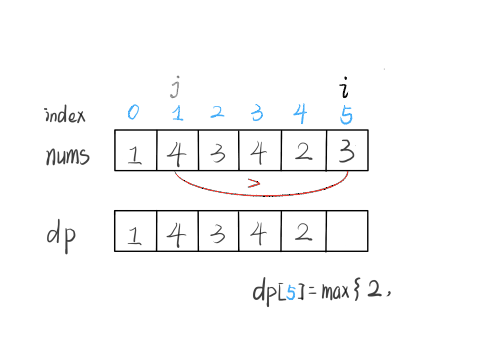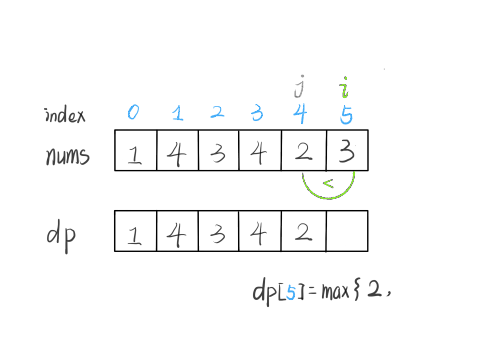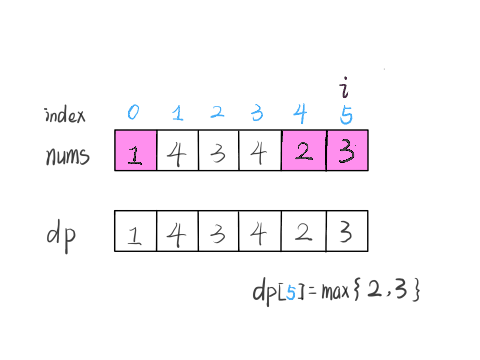
for (int j = 0; j < i; j++) {
    if (nums[i] > nums[j]) 
        dp[i] = Math.max(dp[i], dp[j] + 1);
}

当 i = 5 时，这段代码的逻辑就可以算出 dp[5]。其实到这里，这道算法题我们就基本做完了。

读者也许会问，我们刚才只是算了 dp[5] 呀，dp[4], dp[3] 这些怎么算呢？类似数学归纳法，你已经可以算出 dp[5] 了，其他的就都可以算出来：

for (int i = 0; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) 
            dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

结合我们刚才说的 base case，下面我们看一下完整代码：

public int lengthOfLIS(int[] nums) {
    int[] dp = new int[nums.length];
    // base case：dp 数组全都初始化为 1
    Arrays.fill(dp, 1);
    for (int i = 0; i < nums.length; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) 
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }

    int res = 0;
    for (int i = 0; i < dp.length; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

至此，这道题就解决了，时间复杂度 O(N^2)。总结一下如何找到动态规划的状态转移关系：

**1、**明确 dp 数组所存数据的含义。这一步对于任何动态规划问题都很重要，如果不得当或者不够清晰，会阻碍之后的步骤。

**2、**根据 dp 数组的定义，运用数学归纳法的思想，假设 dp[0...i-1] 都已知，想办法求出 dp[i]，一旦这一步完成，整个题目基本就解决了。

但如果无法完成这一步，很可能就是 dp 数组的定义不够恰当，需要重新定义 dp 数组的含义；或者可能是 dp 数组存储的信息还不够，不足以推出下一步的答案，需要把 dp 数组扩大成二维数组甚至三维数组。

解法2：二分查找解法

这个解法的时间复杂度为 O(NlogN)，但是说实话，正常人基本想不到这种解法（也许玩过某些纸牌游戏的人可以想出来）。所以大家了解一下就好，正常情况下能够给出动态规划解法就已经很不错了。

根据题目的意思，我都很难想象这个问题竟然能和二分查找扯上关系。其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关，甚至有一种排序方法就叫做 patience sorting（耐心排序）。

为了简单起见，后文跳过所有数学证明，通过一个简化的例子来理解一下算法思路。

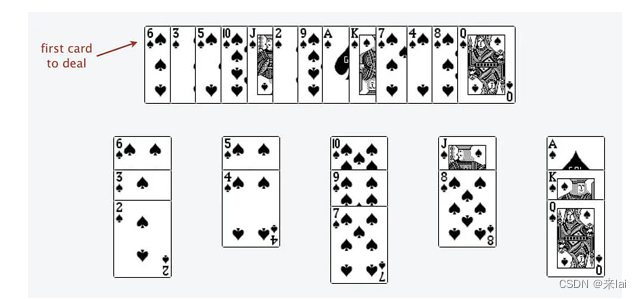
首先，给你一排扑克牌，我们像遍历数组那样从左到右一张一张处理这些扑克牌，最终要把这些牌分成若干堆。

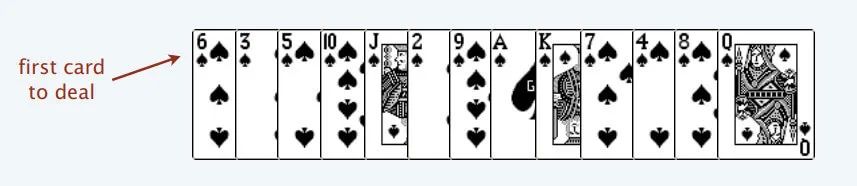
处理这些扑克牌要遵循以下规则：

只能把点数小的牌压到点数比它大的牌上；如果当前牌点数较大没有可以放置的堆，则新建一个堆，把这张牌放进去；如果当前牌有多个堆可供选择，则选择最左边的那一堆放置。

比如说上述的扑克牌最终会被分成这样 5 堆（我们认为纸牌 A 的牌面是最大的，纸牌 2 的牌面是最小的）。

为什么遇到多个可选择堆的时候要放到最左边的堆上呢？稍加观察可以发现，这样可以保证牌堆顶的牌有序（2, 4, 7, 8, Q）。

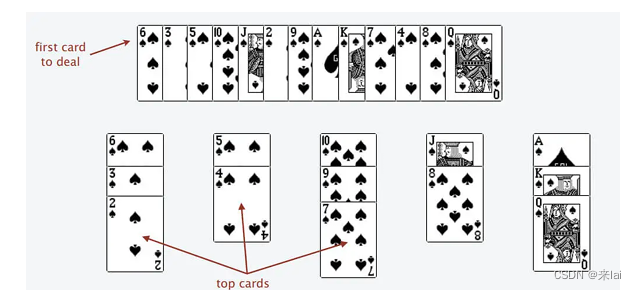
按照上述规则执行，可以算出最长递增子序列，牌的堆数就是最长递增子序列的长度。

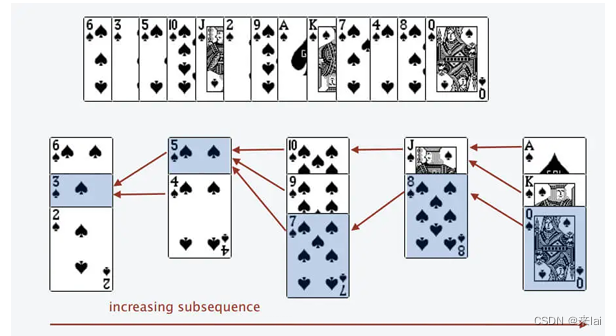
这个应该不难理解，**因为如果从每堆拿出一张牌，就可以形成一个递增子序列。又因为每堆牌的值是递减的，所以这个递增子序列是最长的。**具体证明可点击「阅读原文」查看。

我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗，牌堆顶的牌不是有序吗，这就能用到二分查找了：用二分查找来搜索当前牌应放置的位置。

PS：旧文 我作了首诗，保你闭着眼睛也能写对二分查找 详细介绍了二分查找的细节及变体，这里就完美应用上了，如果没读过强烈建议阅读。

public int lengthOfLIS(int[] nums) {
    int[] top = new int[nums.length];
    // 牌堆数初始化为 0
    int piles = 0;
    for (int i = 0; i < nums.length; i++) {
        // 要处理的扑克牌
        int poker = nums[i];
        /***** 搜索左侧边界的二分查找 *****/
        int left = 0, right = piles;
        while (left < right) {
            int mid = (left + right) / 2;
            if (top[mid] > poker) {
                right = mid;
            } else if (top[mid] < poker) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        /*********************************/
        // 没找到合适的牌堆，新建一堆
        if (left == piles) piles++;
        // 把这张牌放到牌堆顶
        top[left] = poker;
    }
    // 牌堆数就是 LIS 长度
    return piles;
}

至此，二分查找的解法也讲解完毕。

这个解法确实很难想到。首先涉及数学证明，谁能想到按照这些规则执行，就能得到最长递增子序列呢？其次还有二分查找的运用，要是对二分查找的细节不清楚，给了思路也很难写对。

③信封嵌套问题

354.俄罗斯套娃信封问题(300进阶版)

这道题的解法是比较巧妙的：

先对宽度w进行升序排序，如果遇到w相同的情况，则按照高度h降序排序。之后把所有的h作为一个数组，在这个数组上计算 LIS 的长度就是答案。

画个图理解一下，先对这些数对进行排序：

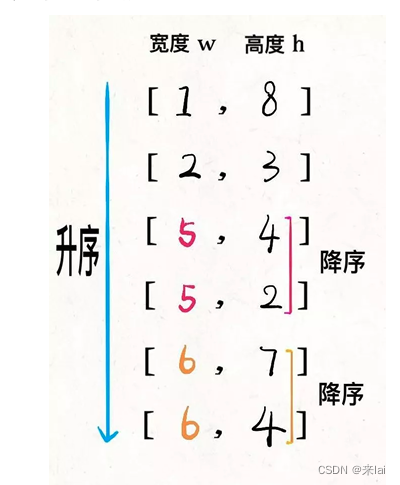
然后在h上寻找最长递增子序列：

这个子序列 [2,3],[5,4],[6,7] 就是最优的嵌套方案。

这个解法的关键在于，对于宽度w相同的数对，要对其高度h进行降序排序。因为两个宽度相同的信封不能相互包含的，而逆序排序保证在w相同的数对中最多只选取一个计入 LIS。

class Solution {
   public static int maxEnvelopes(int[][] envelopes) {
        int n= envelopes.length;
        //按宽度升序排序，如果宽度一样，则按高度降序排序
        Arrays.sort(envelopes, new Comparator<int[]>() {
            public int compare(int[] a, int[] b) {
                //返回 1 原来的默认升序进行调整,变成降序,即 b-a
     			//返回 -1 升序,即 a-b
                return a[0] == b[0]? b[1]- a[1] :a[0] - b[0];
            }
        });
        //对高度数组寻找LIS
        int[] height= new int[n];
        for (int i = 0; i < n; i++) {
            height[i]=envelopes[i][1];
        }
        return lengthOfLIS(height);
    }
    public static int lengthOfLIS(int[] nums) {
        int[] top = new int[nums.length];
        // 牌堆数初始化为 0
        int piles = 0;
        for (int i = 0; i < nums.length; i++) {
            // 要处理的扑克牌
            int poker = nums[i];
            /***** 搜索左侧边界的二分查找 *****/
            int left = 0, right = piles;
            while (left < right) {
                int mid = (left + right) / 2;
                if (top[mid] > poker) {
                    right = mid;
                } else if (top[mid] < poker) {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
            // 没找到合适的牌堆，新建一堆
            if (left == piles) {
                piles++;
            }
            // 把这张牌放到牌堆顶
            top[left] = poker;
        }
        // 牌堆数就是 LIS 长度
        return piles;
    }
}

其实这种问题还可以拓展到三维，比如说现在不是让你嵌套信封，而是嵌套箱子，每个箱子有长宽高三个维度，请你算算最多能嵌套几个箱子？这类问题叫做**「偏序问题」，上升到三维会使难度巨幅提升，需要借助一种高级数据结构「树状数组」**

④最大子数组

53.最大子序和

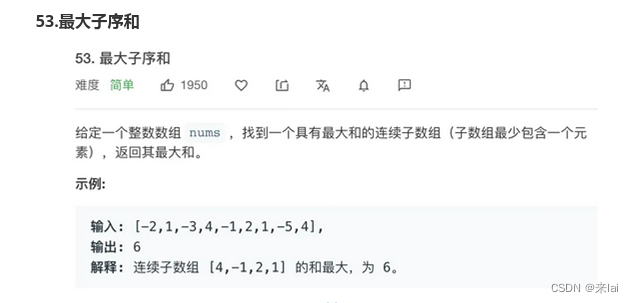
定义dp数组的含义：

以nums[i]为结尾的「最大子数组和」为dp[i]。

这种定义之下，想得到整个nums数组的「最大子数组和」，不能直接返回dp[n-1]，而需要遍历整个dp数组：

int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
    res = Math.max(res, dp[i]);
}
return res;

依然使用数学归纳法来找状态转移关系：假设我们已经算出了dp[i-1]，如何推导出dp[i]呢？

可以做到，dp[i]有两种「选择」，要么与前面的相邻子数组连接，形成一个和更大的子数组；要么不与前面的子数组连接，自成一派，自己作为一个子数组。

如何选择？既然要求「最大子数组和」，当然选择结果更大的那个啦：

// 要么自成一派，要么和前面的子数组合并
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);

综上，我们已经写出了状态转移方程，就可以直接写出解法了：

int maxSubArray(int[] nums) {
    int n = nums.length;
    if (n == 0) return 0;
    int[] dp = new int[n];
    // base case
    // 第一个元素前面没有子数组
    dp[0] = nums[0];
    // 状态转移方程
    for (int i = 1; i < n; i++) {
        dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
    }
    // 得到 nums 的最大子数组
    int res = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

以上解法时间复杂度是 O(N)，空间复杂度也是 O(N)，较暴力解法已经很优秀了，不过注意到dp[i]仅仅和dp[i-1]的状态有关，那么我们可以进行「状态压缩」，将空间复杂度降低：

int maxSubArray(int[] nums) {
    int n = nums.length;
    if (n == 0) return 0;
    // base case
    int dp_0 = nums[0];
    int dp_1 = 0, res = dp_0;

    for (int i = 1; i < n; i++) {
        // dp[i] = max(nums[i], nums[i] + dp[i-1])
        dp_1 = Math.max(nums[i], nums[i] + dp_0);
        dp_0 = dp_1;
        // 顺便计算最大的结果
        res = Math.max(res, dp_1);
    }

    return res;
}

这道「最大子数组和」就和「最长递增子序列」非常类似，dp数组的定义是「以nums[i]为结尾的最大子数组和/最长递增子序列为dp[i]」。因为只有这样定义才能将dp[i+1]和dp[i]建立起联系，利用数学归纳法写出状态转移方程。

⑤最长公共子序列问题

1143.最长公共子序列

给你输入两个字符串s1和s2，请你找出他们俩的最长公共子序列，返回这个子序列的长度。

力扣第 1143 题就是这道题，函数签名如下：

int longestCommonSubsequence(String s1, String s2);

比如说输入s1 = "zabcde", s2 = "acez"，它俩的最长公共子序列是lcs = "ace"，长度为 3，所以算法返回 3。

对于两个字符串求子序列的问题，都是用两个指针i和j分别在两个字符串上移动，大概率是动态规划思路。

最长公共子序列的问题也可以遵循这个规律，我们可以先写一个dp函数：

// 定义：计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j)

这个dp函数的定义是：dp(s1, i, s2, j)计算s1[i..]和s2[j..]的最长公共子序列长度。

根据这个定义，那么我们想要的答案就是dp(s1, 0, s2, 0)，且 base case 就是i == len(s1)或j == len(s2)时，因为这时候s1[i..]或s2[j..]就相当于空串了，最长公共子序列的长度显然是 0：

int longestCommonSubsequence(String s1, String s2) {
    return dp(s1, 0, s2, 0);
}

/* 主函数 */
int dp(String s1, int i, String s2, int j) {
    // base case
    if (i == s1.length() || j == s2.length()) {
        return 0;
    }
    // ...

接下来，咱不要看s1和s2两个字符串，而是要具体到每一个字符，思考每个字符该做什么。

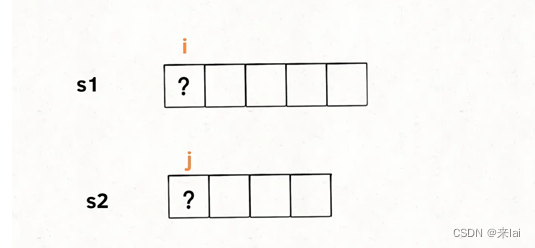
我们只看s1[i]和s2[j]，如果s1[i] == s2[j]，说明这个字符一定在lcs中：

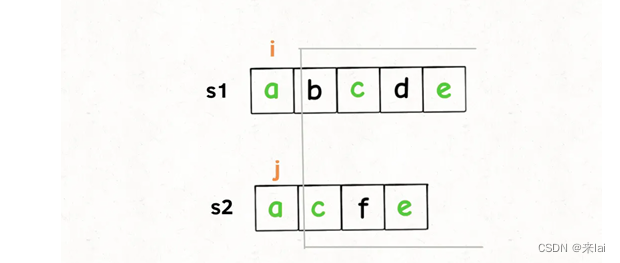
这样，就找到了一个lcs中的字符，根据dp函数的定义，我们可以完善一下代码：

// 定义：计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
    if (s1.charAt(i) == s2.charAt(j)) {
        // s1[i] 和 s2[j] 必然在 lcs 中，
        // 加上 s1[i+1..] 和 s2[j+1..] 中的 lcs 长度，就是答案
        return 1 + dp(s1, i + 1, s2, j + 1);
    } else {
        // ...
    }
}

刚才说的s1[i] == s2[j]的情况，但如果s1[i] != s2[j]，应该怎么办呢？

s1[i] != s2[j]意味着，s1[i]和s2[j]中至少有一个字符不在lcs中：

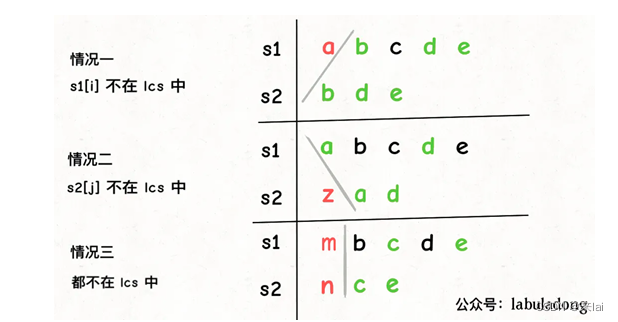
如上图，总共可能有三种情况，我怎么知道具体是那种情况呢？

其实我们也不知道，那就把这三种情况的答案都算出来，取其中结果最大的那个呗，因为题目让我们算「最长」公共子序列的长度嘛。

这三种情况的答案怎么算？回想一下我们的dp函数定义，不就是专门为了计算它们而设计的嘛！

代码可以再进一步：

// 定义：计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
    if (s1.charAt(i) == s2.charAt(j)) {
        return 1 + dp(s1, i + 1, s2, j + 1)
    } else {
        // s1[i] 和 s2[j] 中至少有一个字符不在 lcs 中，
        // 穷举三种情况的结果，取其中的最大结果
        return max(
            // 情况一、s1[i] 不在 lcs 中
            dp(s1, i + 1, s2, j),
            // 情况二、s2[j] 不在 lcs 中
            dp(s1, i, s2, j + 1),
            // 情况三、都不在 lcs 中
            dp(s1, i + 1, s2, j + 1)
        );
    }
}

这里就已经非常接近我们的最终答案了，还有一个小的优化，情况三「s1[i]和s2[j]都不在 lcs 中」其实可以直接忽略。

因为我们在求最大值嘛，情况三在计算s1[i+1..]和s2[j+1..]的lcs长度，这个长度肯定是小于等于情况二s1[i..]和s2[j+1..]中的lcs长度的，因为s1[i+1..]比s1[i..]短嘛，那从这里面算出的lcs当然也不可能更长嘛。

同理，情况三的结果肯定也小于等于情况一。说白了，情况三被情况一和情况二包含了，所以我们可以直接忽略掉情况三，完整代码如下：

// 备忘录，消除重叠子问题
int[][] memo;

/* 主函数 */
int longestCommonSubsequence(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    // 备忘录值为 -1 代表未曾计算
    memo = new int[m][n];
    for (int[] row : memo) 
        Arrays.fill(row, -1);
    // 计算 s1[0..] 和 s2[0..] 的 lcs 长度
    return dp(s1, 0, s2, 0);
}

// 定义：计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
    // base case
    if (i == s1.length() || j == s2.length()) {
        return 0;
    }
    // 如果之前计算过，则直接返回备忘录中的答案
    if (memo[i][j] != -1) {
        return memo[i][j];
    }
    // 根据 s1[i] 和 s2[j] 的情况做选择
    if (s1.charAt(i) == s2.charAt(j)) {
        // s1[i] 和 s2[j] 必然在 lcs 中
        memo[i][j] = 1 + dp(s1, i + 1, s2, j + 1);
    } else {
        // s1[i] 和 s2[j] 至少有一个不在 lcs 中
        memo[i][j] = Math.max(
            dp(s1, i + 1, s2, j),
            dp(s1, i, s2, j + 1)
        );
    }
    return memo[i][j];
}

以上思路完全就是按照我们之前的爆文 动态规划套路框架 来的，应该是很容易理解的。至于为什么要加memo备忘录，我们之前写过很多次，为了照顾新来的读者，这里再简单重复一下，首先抽象出我们核心dp函数的递归框架：

int dp(int i, int j) {
    dp(i + 1, j + 1); // #1
    dp(i, j + 1);     // #2
    dp(i + 1, j);     // #3
}

你看，假设我想从dp(i, j)转移到dp(i+1, j+1)，有不止一种方式，可以直接走#1，也可以走#2 -> #3，也可以走#3 -> #2。

这就是重叠子问题，如果我们不用memo备忘录消除子问题，那么dp(i+1, j+1)就会被多次计算，这是没有必要的。

至此，最长公共子序列问题就完全解决了，用的是自顶向下带备忘录的动态规划思路，我们当然也可以使用自底向上的迭代的动态规划思路，和我们的递归思路一样，关键是如何定义dp数组，我这里也写一下自底向上的解法吧：

定义dp [ i ] [ j ]表示 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列。 （注：text1[0:i-1] 表示的是 text1 的 第 0 个元素到第 i - 1 个元素，两端都包含）

//二维dp数组优
public int longestCommonSubsequence(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    int[][] dp = new int[m + 1][n + 1];
    // 定义：s1[0..i-1] 和 s2[0..j-1] 的 lcs 长度为 dp[i][j]
    // 目标：s1[0..m-1] 和 s2[0..n-1] 的 lcs 长度，即 dp[m][n]
    // base case: dp[0][..] = dp[..][0] = 0
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            // 现在 i 和 j 从 1 开始，所以要减一
            if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                // s1[i-1] 和 s2[j-1] 必然在 lcs 中
                dp[i][j] = 1 + dp[i - 1][j - 1];
            } else {
                // s1[i-1] 和 s2[j-1] 至少有一个不在 lcs 中
                dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
            }
        }
    }
    for (int i = 0; i < m; i++){
        for (int j = 0; j < n; j++){
            System.out.print(dp[i][j] + " ");
        }
        System.out.print("\n");
    }
    return dp[m][n];
}

public int longestCommonSubsequence(String text1, String text2) {
    int m = text1.length(), n = text2.length();
    //dp[i][j]：表示text1[0...i-1]与text2[0...j-1]的最大子序列长度
    int[][] dp = new int[m+1][n+1]; 
    //base case dp[..][0]=dp[0][..]=0;
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if (text1.charAt(i) == text2.charAt(j)) {
                //dp[i+1][j+1]代表 text1[0...i]与text2[0...j]的最大子序列长度
                dp[i+1][j+1] = 1+dp[i][j];
            } else {
                dp[i+1][j+1] = Math.max(dp[i][j + 1], dp[i + 1][j]);
            }
        }
    }
    return dp[m][n];        
}

//dp数组优化一维
public int longestCommonSubsequence(String text1, String text2) {
    int m = text1.length(), n = text2.length();
    //dp[i][j]表示text1[0...i-1]与text2[0...j-1]的最大子序列长度
    int dp[]=new int[n+1];
    for(int i=1;i<=m;i++){
        int pre=dp[0];
        for(int j=1;j<=n;j++){
            int temp=dp[j];
            if(text1.charAt(i-1)==text2.charAt(j-1)){
                dp[j]=1+pre;
            }else{
                dp[j]=Math.max(dp[j],dp[j-1]);
            }
            pre=temp;
        }
    }
    return dp[n];        
}

自底向上的解法中dp数组定义的方式和我们的递归解法有一点差异，而且由于数组索引从 0 开始，有索引偏移，不过思路和我们的递归解法完全相同，如果你看懂了递归解法，这个解法应该不难理解。

另外，自底向上的解法可以通过我们前文讲过的 动态规划状态压缩技巧 来进行优化，把空间复杂度压缩为 O(N)

583.两个字符串的删除操作

这是力扣第 583 题「两个字符串的删除操作」，看下题目：

函数签名如下：

int minDistance(String s1, String s2);

题目让我们计算将两个字符串变得相同的最少删除次数，那我们可以思考一下，最后这两个字符串会被删成什么样子？

删除的结果不就是它俩的最长公共子序列嘛！

那么，要计算删除的次数，就可以通过最长公共子序列的长度推导出来：

int minDistance(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    // 复用前文计算 lcs 长度的函数
    int lcs = longestCommonSubsequence(s1, s2);
    return m - lcs + n - lcs;
}

712.两个字符串的最小ASCII删除和

这道题，和上一道题非常类似，这回不问我们删除的字符个数了，问我们删除的字符的 ASCII 码加起来是多少。

那就不能直接复用计算最长公共子序列的函数了，但是可以依照之前的思路，稍微修改 base case 和状态转移部分即可直接写出解法代码：

// 备忘录
int memo[][];
/* 主函数 */    
int minimumDeleteSum(String s1, String s2) {
    int m = s1.length(), n = s2.length();
    // 备忘录值为 -1 代表未曾计算
    memo = new int[m][n];
    for (int[] row : memo) 
        Arrays.fill(row, -1);

    return dp(s1, 0, s2, 0);
}

// 定义：将 s1[i..] 和 s2[j..] 删除成相同字符串，
// 最小的 ASCII 码之和为 dp(s1, i, s2, j)。
int dp(String s1, int i, String s2, int j) {
    int res = 0;
    // base case
    if (i == s1.length()) {
        // 如果 s1 到头了，那么 s2 剩下的都得删除
        for (; j < s2.length(); j++)
            res += s2.charAt(j);
        return res;
    }
    if (j == s2.length()) {
        // 如果 s2 到头了，那么 s1 剩下的都得删除
        for (; i < s1.length(); i++)
            res += s1.charAt(i);
        return res;
    }

    if (memo[i][j] != -1) {
        return memo[i][j];
    }

    if (s1.charAt(i) == s2.charAt(j)) {
        // s1[i] 和 s2[j] 都是在 lcs 中的，不用删除
        memo[i][j] = dp(s1, i + 1, s2, j + 1);
    } else {
        // s1[i] 和 s2[j] 至少有一个不在 lcs 中，删一个
        memo[i][j] = Math.min(
            s1.charAt(i) + dp(s1, i + 1, s2, j),
            s2.charAt(j) + dp(s1, i, s2, j + 1)
        );
    }
    return memo[i][j];
}

public int minimumDeleteSum(String s1, String s2) {
    int m=s1.length(),n=s2.length();
    int dp[][]=new int[m+1][n+1];
    for(int i=1;i<= m;i++){
        dp[i][0]=dp[i-1][0]+s1.charAt(i-1);
    }
    for(int j=1;j<= n;j++){
        dp[0][j]=dp[0][j-1]+s2.charAt(j-1);
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            if(s1.charAt(i-1)==s2.charAt(j-1)){
                dp[i][j]=dp[i-1][j-1];
            }else{
                dp[i][j]=Math.min(dp[i-1][j] + s1.charAt(i-1),
                                  dp[i][j-1] + s2.charAt(j-1));
            }
        }
    }
    for (int i = 0; i <=m; i++){
        for (int j = 0; j <= n; j++){
            System.out.print(dp[i][j] + " ");
        }
        System.out.print("\n");
    }
    return dp[m][n]; //231=115+t
}

base case 有一定区别，计算lcs长度时，如果一个字符串为空，那么lcs长度必然是 0；但是这道题如果一个字符串为空，另一个字符串必然要被全部删除，所以需要计算另一个字符串所有字符的 ASCII 码之和。

关于状态转移，当s1[i]和s2[j]相同时不需要删除，不同时需要删除，所以可以利用dp函数计算两种情况，得出最优的结果。其他的大同小异，就不具体展开了。

⑥子序列问题模板

1、第一种思路模板是一个一维的 dp 数组：

int n = array.length;
int[] dp = new int[n];

for (int i = 1; i < n; i++) {
    for (int j = 0; j < i; j++) {
        dp[i] = 最值(dp[i], dp[j] + ...)
    }
}

举个我们写过的例子 最长递增子序列，在这个思路中 dp 数组的定义是：

在子数组array[0..i]中，以array[i]结尾的目标子序列（最长递增子序列）的长度是dp[i]。

为啥最长递增子序列需要这种思路呢？前文说得很清楚了，因为这样符合归纳法，可以找到状态转移的关系，这里就不具体展开了。

2、第二种思路模板是一个二维的 dp 数组：

int n = arr.length;
int[][] dp = new dp[n][n];

for (int i = 0; i < n; i++) {
    for (int j = 1; j < n; j++) {
        if (arr[i] == arr[j]) 
            dp[i][j] = dp[i][j] + ...
        else
            dp[i][j] = 最值(...)
    }
}

这种思路运用相对更多一些，尤其是涉及两个字符串/数组的子序列。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。

2.1 涉及两个字符串/数组时（比如最长公共子序列），dp 数组的含义如下：

在子数组arr1[0..i]和子数组arr2[0..j]中，我们要求的子序列（最长公共子序列）长度为dp[i][j]。

2.2 只涉及一个字符串/数组时（比如本文要讲的最长回文子序列），dp 数组的含义如下：

在子数组array[i..j]中，我们要求的子序列（最长回文子序列）的长度为dp[i][j]。

第一种情况可以参考这两篇旧文：详解编辑距离 和 最长公共子序列。

下面就借最长回文子序列这个问题，详解一下第二种情况下如何使用动态规划。

516.最长回文子序列

我们说这个问题对 dp 数组的定义是：在子串s[i..j]中，最长回文子序列的长度为dp[i][j]。一定要记住这个定义才能理解算法。

为啥这个问题要这样定义二维的 dp 数组呢？我们前文多次提到，找状态转移需要归纳思维，说白了就是如何从已知的结果推出未知的部分，这样定义容易归纳，容易发现状态转移关系。

具体来说，如果我们想求dp[i][j]，假设你知道了子问题dp[i+1][j-1]的结果（s[i+1..j-1]中最长回文子序列的长度），你是否能想办法算出dp[i][j]的值（s[i..j]中，最长回文子序列的长度）呢？

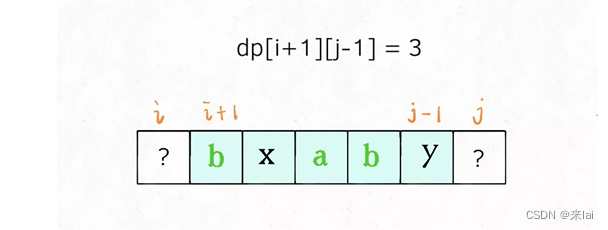
可以！这取决于s[i]和s[j]的字符：

如果它俩相等，那么它俩加上s[i+1..j-1]中的最长回文子序列就是s[i..j]的最长回文子序列：

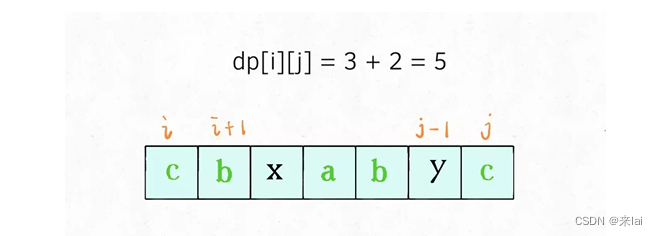
如果它俩不相等，说明它俩不可能同时出现在s[i..j]的最长回文子序列中，那么把它俩分别加入s[i+1..j-1]中，看看哪个子串产生的回文子序列更长即可：

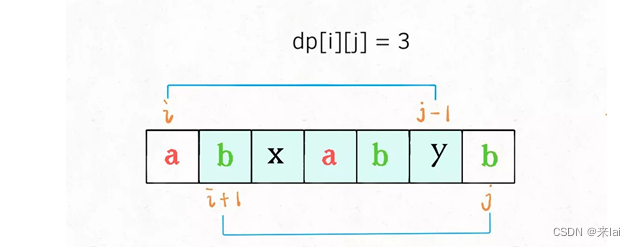
以上两种情况写成代码就是这样：

if (s[i] == s[j])
    // 它俩一定在最长回文子序列中
    dp[i][j] = dp[i + 1][j - 1] + 2;
else
    // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

至此，状态转移方程就写出来了，根据 dp 数组的定义，我们要求的就是dp[0][n - 1]，也就是整个s的最长回文子序列的长度。

代码实现

首先明确一下 base case，如果只有一个字符，显然最长回文子序列长度是 1，也就是dp[i][j] = 1,(i == j)。

因为i肯定小于等于j，所以对于那些i > j的位置，根本不存在什么子序列，应该初始化为 0。

另外，看看刚才写的状态转移方程，想求dp[i][j]需要知道dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1]这三个位置；再看看我们确定的 base case，填入 dp 数组之后是这样：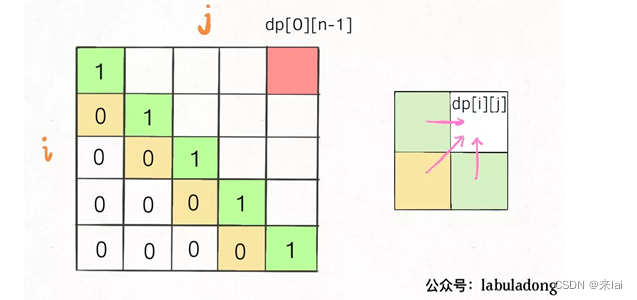

为了保证每次计算dp[i][j]，左、下、左下三个方向的位置已经被计算出来，只能斜着遍历或者反着遍历：

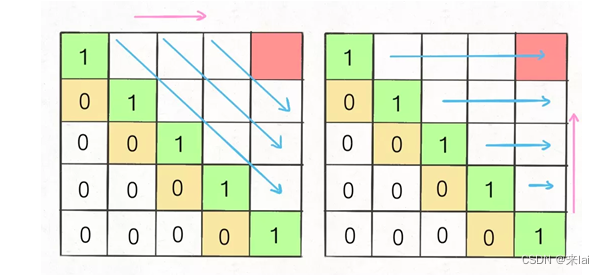
我选择反着遍历，代码如下：

public int longestPalindromeSubseq(String s) {
    int n = s.length();
    // dp 数组全部初始化为 0
    int dp[][] =new int[n][n];
    for(int[] row:dp){
        Arrays.fill(row,0);
    }
    // base case
    for (int i = 0; i < n; i++)
        dp[i][i] = 1;
    // 反着遍历保证正确的状态转移
    for (int i = n - 1; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            // 状态转移方程
            if (s.charAt(i) == s.charAt(j))
                dp[i][j] = dp[i + 1][j - 1] + 2;
            else
                dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
    // 整个 s 的最长回文子串长度
    return dp[0][n - 1];
}

//一维dp数组
int longestPalindromeSubseq(String s) {
    int n = s.length();
    // base case：一维 dp 数组全部初始化为 1
    int[] dp =new int[n];
    Arrays.fill(dp,1);
    for (int i = n - 2; i >= 0; i--) {
        int pre = 0;
        for (int j = i + 1; j < n; j++) {
            int temp = dp[j];
            // 状态转移方程
            if (s.charAt(i) == s.charAt(j))
                dp[j] = pre + 2;
            else
                dp[j] = Math.max(dp[j], dp[j - 1]);
            pre = temp;
        }
    }
    return dp[n - 1];
}

至此，最长回文子序列的问题就解决了。

主要还是正确定义 dp 数组的含义，遇到子序列问题，首先想到两种动态规划思路，然后根据实际问题看看哪种思路容易找到状态转移关系。

另外，找到状态转移和 base case 之后，一定要观察 DP table，看看怎么遍历才能保证通过已计算出来的结果解决新的问题

5.最长回文子串

/*************************************
* 解法1 ：dp数组
*************************************/
public String longestPalindrome(String s) {
    int n=s.length();
    //初始化
    if (n == 0 || n == 1) return s;
    if (n == 2) return (s.charAt(0) == s.charAt(1)) ? s : s.substring(0, 1);
    int maxLen = 1, maxBegin = 0;
    //base case
    /* dp[i][j]表示s[i...j]是否是回文串 */
    boolean[][] dp = new boolean[n][n];
    for (int i = 0; i < n; i++) {
        Arrays.fill(dp[i], true);
    }
    /* i从下往上，j从左往右遍历 */
    for (int i = n - 2; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            dp[i][j] = (dp[i + 1][j - 1] && (s.charAt(i) == s.charAt(j)));
            /* 如果当前子串是回文串，且长度大于maxLen，则更新最长回文串 */
            if (dp[i][j] && (j - i + 1 > maxLen)) {
                maxLen = j - i + 1;
                maxBegin = i;
            }
        }
    }
    // for (int i = 0; i < n; i++){
    //     for (int j = 0; j < n; j++){
    //         System.out.print(dp[i][j] + " ");
    //     }
    //     System.out.print("\n");
    // }
    // dp数组
    // true false true false false 
    // true true false true false 
    // true true true false false 
    // true true true true false 
    // true true true true true 

    return s.substring(maxBegin, maxBegin + maxLen);
}

/*************************************
* 解法2 ：双指针解法（中间扩展法，分奇数偶数）
*************************************/
public String longestPalindrome(String s) {
    String res = "";
    for (int i = 0; i < s.length(); i++) {
        // 以 s[i] 为中心的最长回文子串
        String s1 = palindrome(s, i, i);
        // 以 s[i] 和 s[i+1] 为中心的最长回文子串
        String s2 = palindrome(s, i, i + 1);
        // res = longest(res, s1, s2)
        res = res.length() > s1.length() ? res : s1;
        res = res.length() > s2.length() ? res : s2;
    }
    return res;
}
String palindrome(String s, int left, int right) {
    // 防止索引越界
    while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
        // 向两边展开
        left--;
        right++;
    }
    // 返回以 s[l] 和 s[r] 为中心的最长回文串
    return s.substring(left + 1, right);
}
// int maxLen = 1, maxBegin = 0; //记录最长回文串的长度,起始下标
// public String longestPalindrome(String s) {
//     int n = s.length();
//     for (int i = 0; i < n; i++) {           
//         palindrome(s, i, i);
//         palindrome(s, i, i + 1);
//     }
//     return s.substring(maxBegin, maxBegin + maxLen);
// }
// public void palindrome(String s, int left, int right) {
//     while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
//         left--;
//         right++;
//     }
//     if (right - left - 1 > maxLen) {
//         maxLen = right - left - 1;
//         maxBegin = left + 1;
//     }
// }

=========================================================================================================

1312、674、718、1035、392、115、647 未做

三、背包问题

0-1背包问题

第一步: 要明确两点，「状态」和「选择」。

所以状态有两个，就是「背包的容量」和「可选择的物品」。

选择就是「装进背包」或者「不装进背包」嘛。

明白了状态和选择，动态规划问题基本上就解决了，只要往这个框架套就完事儿了：

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

第二步: 要明确dp数组的定义。

dp数组是什么？其实就是描述问题局面的一个数组。换句话说，我们刚才明确问题有什么「状态」，现在需要用dp数组把状态表示出来。

首先看看刚才找到的「状态」，有两个，也就是说我们需要一个二维dp数组，一维表示可选择的物品，一维表示背包的容量。

dp[i][w]的定义如下：对于前i个物品，当前背包的容量为w，这种情况下可以装的最大价值是dp[i][w]。

比如说，如果 dp[3][5] = 6，其含义为：对于给定的一系列物品中，若只对前 3 个物品进行选择，当背包容量为 5 时，最多可以装下的价值为 6。

PS：为什么要这么定义？便于状态转移，或者说这就是套路，记下来就行了。建议看一下我们的动态规划系列文章，几种动规套路都被扒得清清楚楚了。

根据这个定义，我们想求的最终答案就是**dp[N][W]。base case 就是dp[0][..] = dp[..][0] = 0**，因为没有物品或者背包没有空间的时候，能装的最大价值就是 0。

细化上面的框架：

int dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0

for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            把物品 i 装进背包,
            不把物品 i 装进背包
        )
return dp[N][W]

第三步: 根据「选择」，思考状态转移的逻辑。

简单说就是，上面伪码中「把物品i装进背包」和「不把物品i装进背包」怎么用代码体现出来呢？

这一步要结合对**dp数组的定义和我们的算法逻辑来分析：**

先重申一下刚才我们的dp数组的定义：

dp[i][w]表示：对于前i个物品，当前背包的容量为w时，这种情况下可以装下的最大价值是dp[i][w]。

如果你没有把这第**i个物品装入背包**，那么很显然，最大价值dp[i][w]应该等于dp[i-1][w]。你不装嘛，那就继承之前的结果。

如果你把这第**i个物品装入了背包**，那么dp[i][w]应该等于dp[i-1][w-wt[i-1]] + val[i-1]。

首先，由于i是从 1 开始的，所以对val和wt的取值是i-1。

而dp[i-1][w-wt[i-1]]也很好理解：你如果想装第i个物品，你怎么计算这时候的最大价值？换句话说，在装第**i个物品的前提下，背包能装的最大价值是多少？**

显然，你应该寻求剩余重量w-wt[i-1]限制下能装的最大价值，加上第i个物品的价值val[i-1]，这就是装第i个物品的前提下，背包可以装的最大价值。

综上就是两种选择，我们都已经分析完毕，也就是写出来了状态转移方程，可以进一步细化代码：

for i in [1..N]:
    for w in [1..W]:
        dp[i][w] = max(
            dp[i-1][w],
            dp[i-1][w - wt[i-1]] + val[i-1]
        )
return dp[N][W]

最后一步: 把伪码翻译成代码，处理一些边界情况。

我用java写的代码，把上面的思路完全翻译了一遍，并且处理了w - wt[i-1]可能小于 0 导致数组索引越界的问题：

//01背包：二维dp数组
public int knapsack(int W, int[] wt, int[] val) {
   int N = wt.length;
   int dp[][]=new int[N+1][W+1];
   // 背包重量为0的 dp[i][0]价值为0
   for (int i = 0; i < N ; i++) {
      dp[i][0] = 0;
   }
    for (int i = 1; i <= N; i++) { //物品数量 N
        for (int w = 1; w <= W; w++) { //背包最大容量 W
            if (w - wt[i-1] < 0) {
                // 当前背包容量装不下，只能选择不装入背包
                dp[i][w] = dp[i - 1][w];
            } else {
                /*1、拿：dp[i - 1][w - wt[i-1]]+value[i-1]，
                     寻求剩余重量w-wt[i-1]限制下能装的最大价值，加上第i个物品的价值val[i-1]*/
                //2、不拿： dp[i - 1][w],还是和上个状态一样
                dp[i][w] = Math.max(dp[i-1][w - wt[i-1]] + val[i-1], dp[i-1][w]);
            }
        }
    }
    //打印dp数组
    for (int i = 0; i <= N; i++){
        for (int j = 0; j <= W; j++){
            System.out.print(dp[i][j] + " ");
        }
        System.out.print("\n");
    }
    return dp[N][W];
}

//01背包：一维dp数组优化空间
public int knapsack(int[] wt, int[] val, int W){ //背包最大容量W
    int N = wt.length;//物品数量
    //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
    int[] dp = new int[W + 1];
    //遍历顺序：只能先遍历物品，再倒序遍历背包容量
    for (int i = 0; i < N ; i++){  //物品数量N
        for (int w = W; w >= wt[i]; j--){ //背包最大容量
            dp[w] = Math.max(dp[w - wt[i]] + val[i] , dp[w]);
        }
    }
    //打印dp数组
    for (int j = 0; j <= W; j++){
        System.out.print(dp[j] + " ");
    }
    return dp[W];
}

子集背包问题

那么对于这个问题，我们可以先对集合求和，得出sum，把问题转化为背包问题：

给一个可装载重量为sum/2的背包和N个物品，每个物品的重量为nums[i]。现在让你装物品，是否存在一种装法，能够恰好将背包装满？

第一步要明确两点，「状态」和「选择」。

第二步要明确dp数组的定义。

dp[i][j] = x表示，对于前i个物品，当前背包的容量为j时，若x为true，则说明可以恰好将背包装满，若x为false，则说明不能恰好将背包装满。

比如说，如果dp[4][9] = true，其含义为：对于容量为 9 的背包，若只是用前 4 个物品，可以有一种方法把背包恰好装满。

或者说对于本题，含义是对于给定的集合中，若只对前 4 个数字进行选择，存在一个子集的和可以恰好凑出 9。

根据这个定义，我们想求的最终答案就是dp[N][sum/2]，base case 就是dp[..][0] = true和dp[0][..] = false，因为背包没有空间的时候，就相当于装满了，而当没有物品可选择的时候，肯定没办法装满背包。

第三步，根据「选择」，思考状态转移的逻辑。

如果不把nums[i]算入子集，或者说你不把这第i个物品装入背包，那么是否能够恰好装满背包，取决于上一个状态dp[i-1][j]，继承之前的结果。

如果把nums[i]算入子集，或者说你把这第i个物品装入了背包，那么是否能够恰好装满背包，取决于状态dp[i - 1][j-nums[i-1]]。

首先，由于i是从 1 开始的，而数组索引是从 0 开始的，所以第i个物品的重量应该是nums[i-1]，这一点不要搞混。

dp[i - 1][j-nums[i-1]]也很好理解：你如果装了第i个物品，就要看背包的剩余重量j - nums[i-1]限制下是否能够被恰好装满。

换句话说，如果j - nums[i-1]的重量可以被恰好装满，那么只要把第i个物品装进去，也可恰好装满j的重量；否则的话，重量j肯定是装不满的。

public static boolean canPartition(int[] nums) {
    int sum = 0;
    for (int num : nums) sum += num;
    // 和为奇数时，不可能划分成两个和相等的集合
    if (sum % 2 != 0) return false;
    int n = nums.length;
    sum = sum / 2;
    //初始化
    boolean[][] dp =new boolean[n+1][sum+1];
    for(boolean[] row : dp) {
        Arrays.fill(row,false);
    }
    // base case，因为背包没有空间的时候，就相当于装满了，而当没有物品可选择的时候，肯定没办法装满背包
    for (int i = 0; i <= n; i++)
        dp[i][0] = true;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= sum; j++) {
            if (j - nums[i - 1] < 0) {
                // 背包容量不足，不能装入第 i 个物品
                dp[i][j] = dp[i - 1][j];
            } else {
                // 装入或不装入背包
                dp[i][j] = dp[i - 1][j] || dp[i - 1][j-nums[i-1]];
            }
        }
    }
    return dp[n][sum];
}

再进一步，是否可以优化这个代码呢？注意到dp[i][j]都是通过上一行dp[i-1][..]转移过来的，之前的数据都不会再使用了。

所以，我们可以进行状态压缩，将二维dp数组压缩为一维，节约空间复杂度：

public static boolean canPartition(int[] nums) {
    int sum = 0, n = nums.length;
    for (int num : nums) sum += num;
    if (sum % 2 != 0) return false;
    sum = sum / 2;
    boolean[] dp=new boolean[sum+1];
    Arrays.fill(dp,false);//初始化
    // base case
    dp[0] = true;
    for (int i = 0; i < n; i++)
        for (int j = sum; j >= 0; j--)
            if (j - nums[i] >= 0)
                dp[j] = dp[j] || dp[j - nums[i]];

    return dp[sum];
}

这就是状态压缩，其实这段代码和之前的解法思路完全相同，只在一行dp数组上操作，i每进行一轮迭代，dp[j]其实就相当于dp[i-1][j]，所以只需要一维数组就够用了。

唯一需要注意的是j应该从后往前反向遍历，因为每个物品（或者说数字）只能用一次，以免之前的结果影响其他的结果。

至此，子集切割的问题就完全解决了，时间复杂度 O(n*sum)，空间复杂度 O(sum)。

完全背包问题

518 . 零钱兑换II

有一个背包，最大容量为amount，有一系列物品coins，每个物品的重量为coins[i]，每个物品的数量无限。请问有多少种方法，能够把背包恰好装满？

第一步要明确两点，「状态」和「选择」。

这部分都是背包问题的老套路了，我还是啰嗦一下吧：

状态有两个，就是「背包的容量」和「可选择的物品」，选择就是「装进背包」或者「不装进背包」。

明白了状态和选择，动态规划问题基本上就解决了，只要往这个框架套就完事儿了：

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 计算(选择1，选择2...)

第二步要明确**dp数组的定义**。

首先看看刚才找到的「状态」，有两个，也就是说我们需要一个二维dp数组。

dp[i][j]的定义如下：

若只使用前i个物品，当背包容量为j时，有dp[i][j]种方法可以装满背包。

换句话说，翻译回我们题目的意思就是：

若只使用coins中的前i个硬币的面值，若想凑出金额j，有dp[i][j]种凑法。

经过以上的定义，可以得到：

base case 为dp[0][..] = 0， dp[..][0] = 1。因为如果不使用任何硬币面值，就无法凑出任何金额；如果凑出的目标金额为 0，那么“无为而治”就是唯一的一种凑法。

我们最终想得到的答案就是dp[N][amount]，其中N为coins数组的大小。

大致的伪码思路如下：

int dp[N+1][amount+1]
dp[0][..] = 0
dp[..][0] = 1

for i in [1..N]:
    for j in [1..amount]:
        把物品 i 装进背包,
        不把物品 i 装进背包
return dp[N][amount]

第三步，根据「选择」，思考状态转移的逻辑。

注意，我们这个问题的特殊点在于物品的数量是无限的，所以这里和之前写的背包问题文章有所不同。

如果你不把这第i个物品装入背包，也就是说你不使用coins[i]这个面值的硬币，那么凑出面额j的方法数dp[i][j]应该等于dp[i-1][j]，继承之前的结果。

如果你把这第i个物品装入了背包，也就是说你使用coins[i]这个面值的硬币，那么dp[i][j]应该等于dp[i][j-coins[i-1]]。

首先由于i是从 1 开始的，所以coins的索引是i-1时表示第i个硬币的面值。

dp[i][j-coins[i-1]]也不难理解，如果你决定使用这个面值的硬币，那么就应该关注如何凑出金额j - coins[i-1]。

比如说，你想用面值为 2 的硬币凑出金额 5，那么如果你知道了凑出金额 3 的方法，再加上一枚面额为 2 的硬币，不就可以凑出 5 了嘛。

综上就是两种选择，而我们想求的dp[i][j]是「共有多少种凑法」，所以dp[i][j]的值应该是以上两种选择的结果之和：

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= amount; j++) {
        if (j - coins[i-1] >= 0)
            dp[i][j] = dp[i - 1][j] 
                     + dp[i][j-coins[i-1]];
return dp[N][W]

最后一步，把伪码翻译成代码，处理一些边界情况。

我用 Java 写的代码，把上面的思路完全翻译了一遍，并且处理了一些边界问题：

int change(int amount, int[] coins) {
    int n = coins.length;
    int[][] dp = int[n + 1][amount + 1];
    // base case
    for (int i = 0; i <= n; i++) 
        dp[i][0] = 1;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= amount; j++)
            if (j - coins[i-1] >= 0)
                dp[i][j] = dp[i - 1][j] 
                         + dp[i][j - coins[i-1]];
            else 
                dp[i][j] = dp[i - 1][j];
    }
    return dp[n][amount];
}

而且，我们通过观察可以发现，dp数组的转移只和dp[i][..]和dp[i-1][..]有关，所以可以压缩状态，进一步降低算法的空间复杂度：

int change(int amount, int[] coins) {
    int n = coins.length;
    int[] dp = new int[amount + 1];
    dp[0] = 1; // base case
    for (int i = 0; i < n; i++)
        for (int j = 1; j <= amount; j++)
            if (j - coins[i] >= 0)
                dp[j] = dp[j] + dp[j-coins[i]];
    
    return dp[amount];
}

这个解法和之前的思路完全相同，将二维dp数组压缩为一维，时间复杂度 O(N*amount)，空间复杂度 O(amount)。

扩展：

39. 组合总和

利用回溯算法+剪枝

//回溯算法 + 剪枝
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    int len = candidates.length;
    List<List<Integer>> res = new ArrayList<>();
    if (len == 0) {
        return res;
    }
    // 排序是剪枝的前提
    Arrays.sort(candidates);

    Deque<Integer> path = new ArrayDeque<>();
    dfs(candidates, 0, target, path, res);
    return res;
}
private void dfs(int[] candidates, int begin, int target, Deque<Integer> path,  List<List<Integer>> res) {
    int len=candidates.length;
    // target 为负数和 0 的时候不再产生新的孩子结点
    if (target < 0) {
        return;
    }
    if (target == 0) {
        res.add(new ArrayList<>(path));
        return;
    }

    // 重点理解这里从 begin 开始搜索的语意
    for (int i = begin; i < len; i++) {
        // 重点理解这里剪枝，前提是候选数组已经有序，
        if (target - candidates[i] < 0) {
            break;
        }

        path.addLast(candidates[i]);
        // 注意：由于每一个元素可以重复使用，下一轮搜索的起点依然是 i，这里非常容易弄错
        dfs(candidates, i, target - candidates[i], path, res);
        // 状态重置
        path.removeLast();
    }
}

四、贪心问题

什么是贪心算法呢？贪心算法可以认为是动态规划算法的一个特例，相比动态规划，使用贪心算法需要满足更多的条件（贪心选择性质），但是效率比动态规划要高。

比如说一个算法问题使用暴力解法需要指数级时间，如果能使用动态规划消除重叠子问题，就可以降到多项式级别的时间，如果满足贪心选择性质，那么可以进一步降低时间复杂度，达到线性级别的。

什么是贪心选择性质呢，简单说就是：每一步都做出一个局部最优的选择，最终的结果就是全局最优。注意哦，这是一种特殊性质，其实只有一小部分问题拥有这个性质。

比如你面前放着 100 张人民币，你只能拿十张，怎么才能拿最多的面额？显然每次选择剩下钞票中面值最大的一张，最后你的选择一定是最优的。

然而，大部分问题都明显不具有贪心选择性质。比如打斗地主，对手出对儿三，按照贪心策略，你应该出尽可能小的牌刚好压制住对方，但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法，而得使用动态规划解决，参见前文 动态规划解决博弈问题。

区间调度

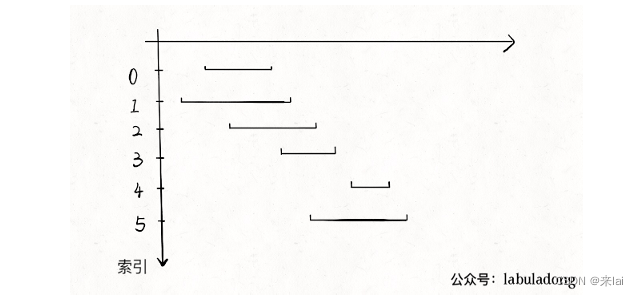
正确的思路其实很简单，可以分为以下三步：

1. 从区间集合 intvs 中选择一个区间 x，这个 x 是在当前所有区间中结束最早的（end 最小）。
2. 把所有与 x 区间相交的区间从区间集合 intvs 中删除。
3. 重复步骤 1 和 2，直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。

把这个思路实现成算法的话，可以按每个区间的end数值升序排序，因为这样处理之后实现步骤 1 和步骤 2 都方便很多:

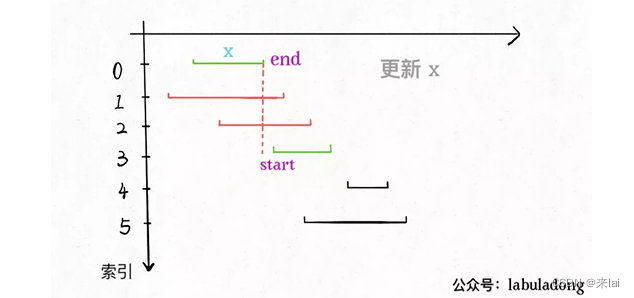
现在来实现算法，对于步骤 1，由于我们预先按照end排了序，所以选择 x 是很容易的。关键在于，如何去除与 x 相交的区间，选择下一轮循环的 x 呢？

由于我们事先排了序，不难发现所有与 x 相交的区间必然会与 x 的end相交；如果一个区间不想与 x 的end相交，它的start必须要大于（或等于）x 的end：

435 、无重叠区间

public int eraseOverlapIntervals(int[][] intervals) {
    int n = intervals.length;
    return n - intervalSchedule(intervals);
}
public int intervalSchedule(int[][] intvs) {
    if (intvs.length == 0) return 0;
    // 按 end 升序排序,避免 return a[1] - b[1] 时 int 型溢出， 换用 < 等运算符来比较。
    Arrays.sort(intvs, new Comparator<int[]>() {
        public int compare(int[] a, int[] b) {
            return a[1] < b[1] ? -1 :1;
            //return a[1] - b[1];
        }
    });
    // 至少有一个区间不相交
    int count = 1;
    // 排序后，第一个区间就是 x
    int x_end = intvs[0][1];
    for (int[] interval : intvs) {
        int start = interval[0];
        if (start >= x_end) {
            // 找到下一个选择的区间了
            count++;
            x_end = interval[1];
        }
    }
    return count;
}

452 、用最少的箭头射爆气球

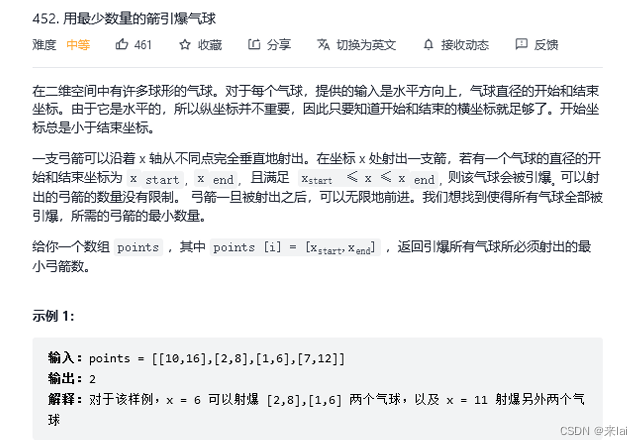
int findMinArrowShots(int[][] intvs) {
    if (intvs.length == 0) return 0;
    // 按 end 升序排序,避免 return a[1] - b[1] 时 int 型溢出， 换用 < 等运算符来比较。
    Arrays.sort(intvs, new Comparator<int[]>() {
        public int compare(int[] a, int[] b) {
            return a[1] < b[1] ? -1 :1;
            //return a[1] - b[1];
        }
    });
    // 至少有一个区间不相交
    int count = 1;
    // 排序后，第一个区间就是 x
    int x_end = intvs[0][1];

    for (int[] interval : intvs) {
        int start = interval[0];
        // 把 >= 改成 > 就行了
        if (start > x_end) {
            count++;
            x_end = interval[1];
        }
    }
    return count;
}

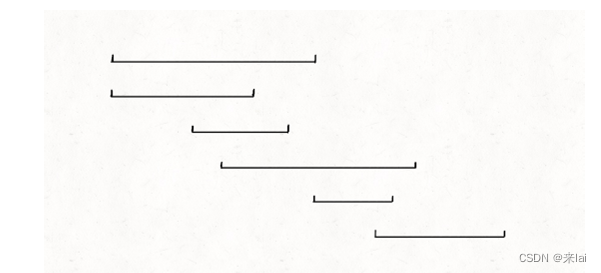
视频拼接

1024. 视频拼接

至于到底如何排序，这个就要因题而异了，我做这道题的思路是先按照起点升序排序，如果起点相同的话按照终点降序排序。

为什么这样排序呢，主要考虑到这道题的以下两个特点：

1、要用若干短视频凑出完成视频[0, T]，至少得有一个短视频的起点是 0。

这个很好理解，如果没有一个短视频是从 0 开始的，那么区间[0, T]肯定是凑不出来的。

2、如果有几个短视频的起点都相同，那么一定应该选择那个最长（终点最大）的视频。

这一条就是贪心的策略，因为题目让我们计算最少需要的短视频个数，如果起点相同，那肯定是越长越好，不要白不要，多出来了大不了剪辑掉嘛。

基于以上两个特点，将clips按照起点升序排序，起点相同的按照终点降序排序，最后得到的区间顺序就像这样：

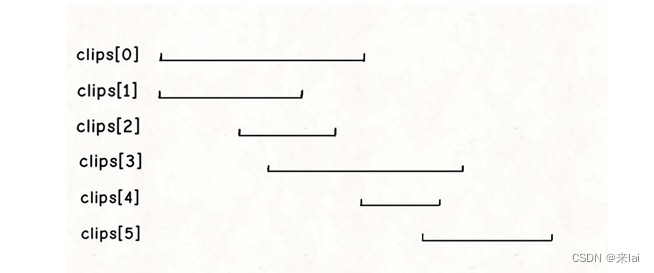
这样我们就可以确定，如果clips[0]是的起点是 0，那么clips[0]这个视频一定会被选择。

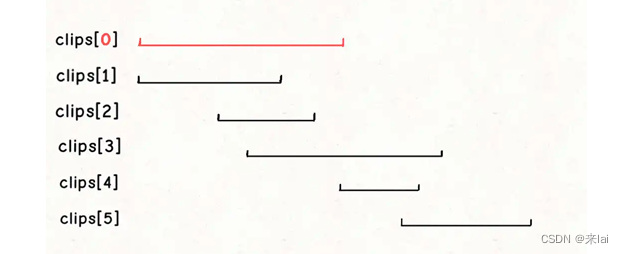
当我们确定clips[0]一定会被选择之后，就可以选出第二个会被选择的视频：

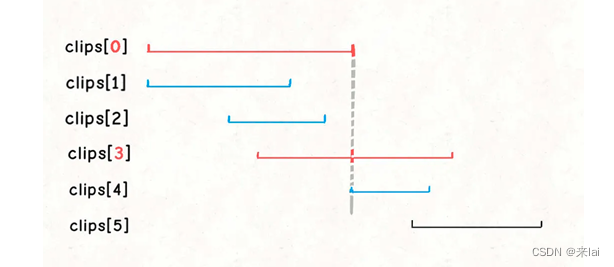
我们会比较所有起点小于clips[0][1]的区间，根据贪心策略，它们中终点最大的那个区间就是第二个会被选中的视频。

然后可以通过第二个视频区间贪心选择出第三个视频，以此类推，直到覆盖区间[0, T]，或者无法覆盖返回 -1。

以上就是这道题的解题思路，仔细想想，这题的核心和前文 贪心算法玩跳跃游戏 写的跳跃游戏是相同的，如果你能看出这两者的联系，就可以说理解贪心算法的奥义了。

实现上述思路需要我们用两个变量curEnd和nextEnd来进行：

最终代码实现如下：

public int videoStitching(int[][] clips, int time) {
    if (time == 0) return 0;
    // 按起点升序排列，起点相同的降序排列
    Arrays.sort(clips, (a, b) -> {
        // if (a[0] == b[0]) {
        //     return b[1] - a[1];
        // }
        // return a[0] - b[0];
        return a[0] == b[0] ? b[1]-a[1] : a[0]-b[0];
    });
    // 记录选择的短视频个数
    int res = 0;
    //{0,2},{1,9},{1,5},{4,6},{5,9},{8,10}
    int curEnd=0,nextEnd = 0;
    int i=0 , n=clips.length;
    while (i < n && clips[i][0] <= curEnd) {
        // 在第 res 个视频的区间内贪心选择下一个视频
        while (i < n && clips[i][0] <= curEnd) {
            nextEnd = Math.max(nextEnd, clips[i][1]);
            i++;
        }
        // 找到下一个视频，更新 curEnd
        res++;
        curEnd = nextEnd;
        if (curEnd >= time) {
            // 已经可以拼出区间 [0, T]
            return res;
        }
    }
    // 无法连续拼出区间 [0, T]
    return -1;
}

区间问题：1288.删除被覆盖区间、56.区间合并、986.区间交集

贪心算法的区间问题：435.区间调度，1024.视频拼接、55.跳跃游戏

跳跃游戏

55.跳跃游戏

不知道读者有没有发现，有关动态规划的问题，大多是让你求最值的，比如最长子序列，最小编辑距离，最长公共子串等等等。这就是规律，因为动态规划本身就是运筹学里的一种求最值的算法。

那么贪心算法作为特殊的动态规划也是一样，一般也是让你求个最值。这道题表面上不是求最值，但是可以改一改：

请问通过题目中的跳跃规则，最多能跳多远？如果能够越过最后一格，返回 true，否则返回 false。

所以说，这道题肯定可以用动态规划求解的。但是由于它比较简单，下一道题再用动态规划和贪心思路进行对比，现在直接上贪心的思路：

bool canJump(int[] nums) {
    int n = nums.length;
    int farthest = 0;
    for (int i = 0; i < n - 1; i++) {
        // 不断计算能跳到的最远距离
        farthest = Math.max(farthest, i + nums[i]);
        // 可能碰到了 0，卡住跳不动了
        if (farthest <= i) return false;
    }
    return farthest >= n - 1;
}

你别说，如果之前没有做过类似的题目，还真不一定能够想出来这个解法。每一步都计算一下从当前位置最远能够跳到哪里，然后和一个全局最优的最远位置farthest做对比，通过每一步的最优解，更新全局最优解，这就是贪心。

45.跳跃游戏II

现在的问题是，保证你一定可以跳到最后一格，请问你最少要跳多少次，才能跳过去？

我们先来说说动态规划的思路，采用自顶向下的递归动态规划，可以这样定义一个dp函数：

// 定义：从索引 p 跳到最后一格，至少需要 dp(nums, p) 步
int dp(int[] nums, int p);

我们想求的结果就是dp(nums, 0)，base case 就是当p超过最后一格时，不需要跳跃：

if (p >= nums.length - 1) {
    return 0;
}

根据前文 动态规划套路详解 的动规框架，就可以暴力穷举所有可能的跳法，通过备忘录memo消除重叠子问题，取其中的最小值最为最终答案：

int[] memo;
public int jump(int[] nums) {
    int n = nums.length;
    // 备忘录都初始化为 n，相当于 INT_MAX
    // 因为从 0 调到 n - 1 最多 n - 1 步
    memo = new int[n];
    Arrays.fill(memo, n);
    return dp(nums, 0);
}
public int dp(int[] nums, int p) {
    int n = nums.length;
    // base case
    if (p >= n - 1) {
        return 0;
    }
    // 子问题已经计算过
    if (memo[p] != n) {
        return memo[p];
    }
    int steps = nums[p];
    // 你可以选择跳 1 步，2 步...
    for (int i = 1; i <= steps; i++) {
        // 穷举每一个选择
        // 计算每一个子问题的结果
        int subProblem = dp(nums, p + i);
        // 取其中最小的作为最终结果
        memo[p] = Math.min(memo[p], subProblem + 1);
    }
    return memo[p];
}

这个动态规划应该很明显了，按照 动态规划套路详解 所说的套路，状态就是当前所站立的索引p，选择就是可以跳出的步数。

该算法的时间复杂度是 递归深度 × 每次递归需要的时间复杂度，即 O(N^2)，在 LeetCode 上是无法通过所有用例的，会超时。

贪心算法比动态规划多了一个性质：贪心选择性质。我知道大家都不喜欢看严谨但枯燥的数学形式定义，那么我们就来直观地看一看什么样的问题满足贪心选择性质。

刚才的动态规划思路，不是要穷举所有子问题，然后取其中最小的作为结果吗？核心的代码框架是这样：

int steps = nums[p];
// 你可以选择跳 1 步，2 步...
for (int i = 1; i <= steps; i++) {
    // 计算每一个子问题的结果
    int subProblem = dp(nums, p + i);
    res = min(subProblem + 1, res);
}

for 循环中会陷入递归计算子问题，这是动态规划时间复杂度高的根本原因。

但是，真的需要「递归地」计算出每一个子问题的结果，然后求最值吗？直观地想一想，似乎不需要递归，只需要判断哪一个选择最具有「潜力」即可：

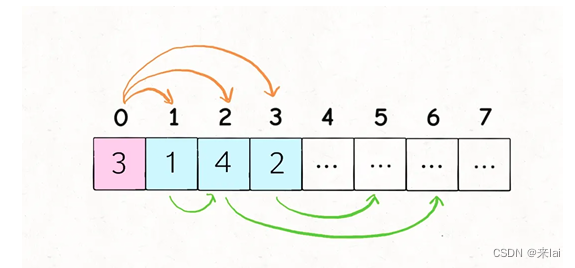
比如上图这种情况应该跳多少呢？

显然应该跳 2 步调到索引 2，因为**nums[2]的可跳跃区域涵盖了索引区间[3..6]，比其他的都大**。如果想求最少的跳跃次数，那么往索引 2 跳必然是最优的选择。

你看，这就是贪心选择性质，我们不需要「递归地」计算出所有选择的具体结果然后比较求最值，而只需要做出那个最有「潜力」，看起来最优的选择即可。

绕过这个弯儿来，就可以写代码了：

int jump(int[] nums) {
    int n = nums.length;
    int end = 0, farthest = 0;
    int jumps = 0;
    for (int i = 0; i < n - 1; i++) {
        farthest = Math.max(nums[i] + i, farthest);
        if (end == i) {
            jumps++;
            end = farthest;
        }
    }
    return jumps;
}

结合刚才那个图，就知道这段短小精悍的代码在干什么了：

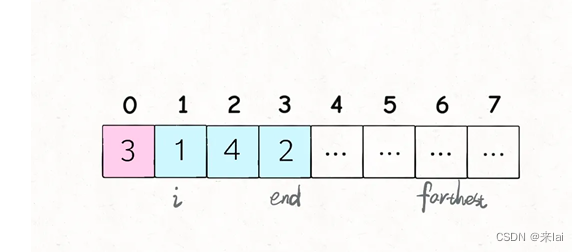
i和end标记了可以选择的跳跃步数，farthest标记了所有可选择跳跃步数[i..end]中能够跳到的最远距离，jumps记录了跳跃次数。

本算法的时间复杂度 O(N)，空间复杂度 O(1)，可以说是非常高效，动态规划都被吊起来打了。

至此，两道跳跃问题都使用贪心算法解决了。

加油站

134.加油站

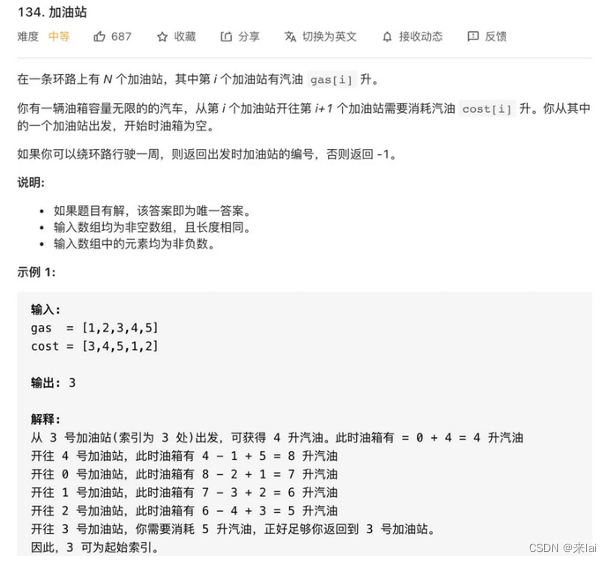
题目应该不难理解，就是每到达一个站点i，可以加gas[i]升油，但离开站点i需要消耗cost[i]升油，问你从哪个站点出发，可以兜一圈回来。

要说暴力解法，肯定很容易想到，用一个 for 循环遍历所有站点，假设为起点，然后再套一层 for 循环，判断一下是否能够转一圈回到起点：

int n = gas.length;
for (int start = 0; start < n; start++) {
    for (int step = 0; step < n; step++) {
        int i = (start + step) % n;
        tank += gas[i];
        tank -= cost[i];
        // 判断油箱中的油是否耗尽
    }
}

很明显时间复杂度是 O(N^2)，这么简单粗暴的解法一定不是最优的，我们试图分析一下是否有优化的余地。

暴力解法是否有重复计算的部分？是否可以抽象出「状态」，是否对同一个「状态」重复计算了多次？

我们前文 动态规划详解 说过，变化的量就是「状态」。那么观察这个暴力穷举的过程，变化的量有两个，分别是「起点」和「当前油箱的油量」，但这两个状态的组合肯定有不下 O(N^2) 种，显然没有任何优化的空间。

所以说这道题肯定不是通过简单的剪枝来优化暴力解法的效率，而是需要我们发现一些隐藏较深的规律，从而减少一些冗余的计算。

下面我们介绍两种方法巧解这道题，分别是数学图像解法和贪心解法。

图像解法

汽车进入站点i可以加gas[i]的油，离开站点会损耗cost[i]的油，那么可以把站点和与其相连的路看做一个整体，将gas[i] - cost[i]作为经过站点i的油量变化值：

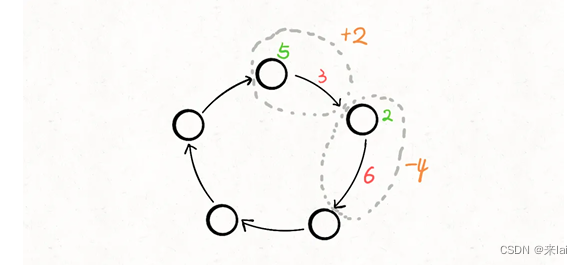
这样，题目描述的场景就被抽象成了一个环形数组，数组中的第i个元素就是gas[i] - cost[i]。

有了这个环形数组，我们需要判断这个环形数组中是否能够找到一个起点start，使得从这个起点开始的累加和一直大于等于 0。

如何判断是否存在这样一个起点start？又如何计算这个起点start的值呢？

我们不妨就把 0 作为起点，计算累加和的代码非常简单：

int n = gas.length, sum = 0;
for (int i = 0; i < n; i++) {
    // 计算累加和
    sum += gas[i] - cost[i];
}

sum就相当于是油箱中油量的变化，上述代码中sum的变化过程可能是这样的：

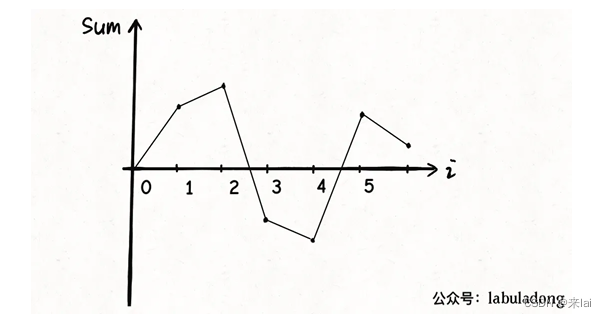
显然，上图将 0 作为起点肯定是不行的，因为sum在变化的过程中小于 0 了，不符合我们「累加和一直大于等于 0」的要求。

那如果 0 不能作为起点，谁可以作为起点呢？

看图说话，图像的最低点最有可能可以作为起点：

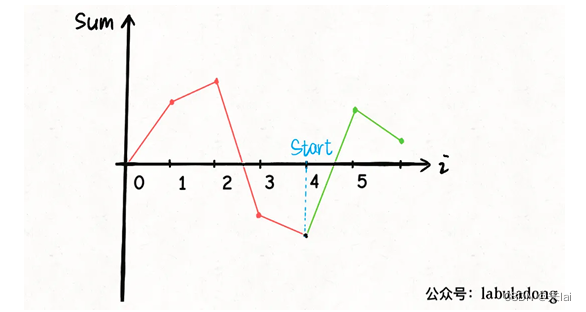
如果把这个「最低点」作为起点，就是说将这个点作为坐标轴原点，就相当于把图像「最大限度」向上平移了。

再加上这个数组是环形数组，最低点左侧的图像可以接到图像的最右侧：

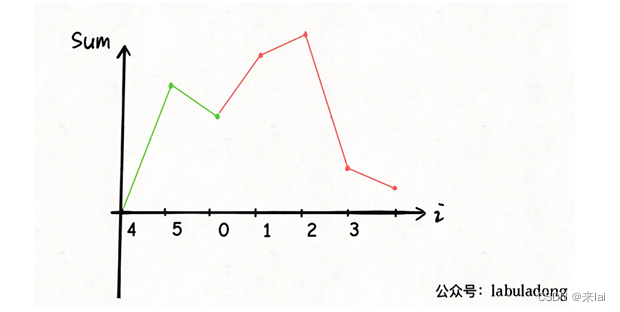
这样，整个图像都保持在 x 轴以上，所以这个最低点 4，就是题目要求我们找的起点。

不过，经过平移后图像一定全部在 x 轴以上吗？不一定，因为还有无解的情况：

如果sum(gas[...]) < sum(cost[...])，总油量小于总的消耗，那肯定是没办法环游所有站点的。

综上，我们就可以写出代码：

int canCompleteCircuit(int[] gas, int[] cost) {
    int n = gas.length;
    // 相当于图像中的坐标点和最低点
    int sum = 0, minSum = 0;
    int start = 0;
    for (int i = 0; i < n; i++) {
        sum += gas[i] - cost[i];
        if (sum < minSum) {
            // 经过第 i 个站点后，使 sum 到达新低
            // 所以站点 i + 1 就是最低点（起点）
            start = i + 1;
            minSum = sum;
        }
    }
    if (sum < 0) {
        // 总油量小于总的消耗，无解
        return -1;
    }
    // 环形数组特性
    return start == n ? 0 : start;
}

以上是观察函数图像得出的解法，时间复杂度为 O(N)，比暴力解法的效率高很多。

下面我们介绍一种使用贪心思路写出的解法，和上面这个解法比较相似，不过分析过程不尽相同。

贪心解法

用贪心思路解决这道题的关键在于以下这个结论：

如果选择站点i作为起点「恰好」无法走到站点j，那么i和j中间的任意站点k都不可能作为起点。

比如说，如果从站点1出发，走到站点5时油箱中的油量「恰好」减到了负数，那么说明站点1「恰好」无法到达站点5；那么你从站点2,3,4任意一个站点出发都无法到达5，因为到达站点5时油箱的油量也必然被减到负数。

如何证明这个结论？

假设tank记录当前油箱中的油量，如果从站点i出发（tank = 0），走到j时恰好出现tank < 0的情况，那说明走到i, j之间的任意站点k时都满足tank > 0，对吧。

如果把k作为起点的话，相当于在站点k时tank = 0，那走到j时必然有tank < 0，也就是说k肯定不能是起点。

拜托，从i出发走到k好歹tank > 0，都无法达到j，现在你还让tank = 0了，那更不可能走到j了对吧。

综上，这个结论就被证明了。

回想一下我们开头说的暴力解法是怎么做的？

如果我发现从i出发无法走到j，那么显然i不可能是起点。

现在，我们发现了一个新规律，可以推导出什么？

如果我发现从i出发无法走到j，那么i以及i, j之间的所有站点都不可能作为起点。

看到冗余计算了吗？看到优化的点了吗？

这就是贪心思路的本质，如果找不到重复计算，那就通过问题中一些隐藏较深的规律，来减少冗余计算。

根据这个结论，就可以写出如下代码：

int canCompleteCircuit(int[] gas, int[] cost) {
    int n = gas.length;
    int sum = 0;
    for (int i = 0; i < n; i++) {
        sum += gas[i] - cost[i];
    }
    if (sum < 0) {
        // 总油量小于总的消耗，无解
        return -1;
    }
    // 记录油箱中的油量
    int tank = 0;
    // 记录起点
    int start = 0;
    for (int i = 0; i < n; i++) {
        tank += gas[i] - cost[i];
        if (tank < 0) {
            // 无法从 start 走到 i
            // 所以站点 i + 1 应该是起点
            tank = 0;
            start = i + 1;
        }
    }
    return start == n ? 0 : start;
}

这个解法的时间复杂度也是 O(N)，和之前图像法的解题思路有所不同，但代码非常类似。

其实，你可以把这个解法的思路结合图像来思考，可以发现它们本质上是一样的，只是理解方式不同而已。

对于这种贪心算法，没有特别套路化的思维框架，主要还是靠多做题多思考，将题目的场景进行抽象的联想，找出隐藏其中的规律，从而减少计算量，进行效率优化。

五、用动态规划解决问题

64.最小路径和

一般来说，让你在二维矩阵中求最优化问题（最大值或者最小值），肯定需要递归 + 备忘录，也就是动态规划技巧。

就拿题目举的例子来说，我给图中的几个格子编个号方便描述：

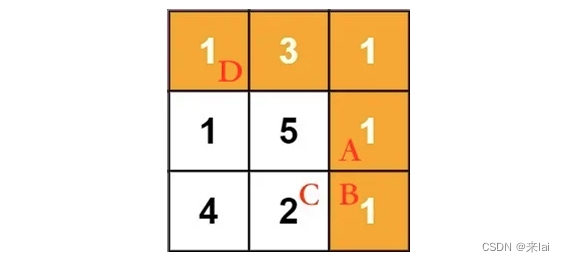
我们想计算从起点D到达B的最小路径和，那你说怎么才能到达B呢？

题目说了只能向右或者向下走，所以只有从A或者C走到B。

那么算法怎么知道从A走到B才能使路径和最小，而不是从C走到B呢？

难道是因为位置A的元素大小是 1，位置C的元素是 2，1 小于 2，所以一定要从A走到B才能使路径和最小吗？

其实不是的，真正的原因是，从D走到A的最小路径和是 6，而从D走到C的最小路径和是 8，6 小于 8，所以一定要从A走到B才能使路径和最小。

换句话说，我们把「从D走到B的最小路径和」这个问题转化成了「从D走到A的最小路径和」和 「从D走到C的最小路径和」这两个问题。

理解了上面的分析，这不就是状态转移方程吗？所以这个问题肯定会用到动态规划技巧来解决。

比如我们定义如下一个dp函数：

int dp(int[][] grid, int i, int j);

这个dp函数的定义如下：

从左上角位置(0, 0)走到位置(i, j)的最小路径和为dp(grid, i, j)。

根据这个定义，我们想求的最小路径和就可以通过调用这个dp函数计算出来：

int minPathSum(int[][] grid) {
    int m = grid.length;
    int n = grid[0].length;
    // 计算从左上角走到右下角的最小路径和
    return dp(grid, m - 1, n - 1);
}

再根据刚才的分析，很容易发现，dp(grid, i, j)的值取决于dp(grid, i - 1, j)和dp(grid, i, j - 1)返回的值。

我们可以直接写代码了：

int dp(int[][] grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        return grid[0][0];
    }
    // 如果索引出界，返回一个很大的值，
    // 保证在取 min 的时候不会被取到
    if (i < 0 || j < 0) {
        return Integer.MAX_VALUE;
    }

    // 左边和上面的最小路径和加上 grid[i][j]
    // 就是到达 (i, j) 的最小路径和
    return Math.min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j];
}

上述代码逻辑已经完整了，接下来就分析一下，这个递归算法是否存在重叠子问题？是否需要用备忘录优化一下执行效率？

前文多次说过判断重叠子问题的技巧，首先抽象出上述代码的递归框架：

int dp(int i, int j) {
    dp(i - 1, j); // #1
    dp(i, j - 1); // #2
}

如果我想从dp(i, j)递归到dp(i-1, j-1)，有几种不同的递归调用路径？

可以是dp(i, j) -> #1 -> #2或者dp(i, j) -> #2 -> #1，不止一种，说明dp(i-1, j-1)会被多次计算，所以一定存在重叠子问题。

那么我们可以使用备忘录技巧进行优化：

int[][] memo;

int minPathSum(int[][] grid) {
    int m = grid.length;
    int n = grid[0].length;
    // 构造备忘录，初始值全部设为 -1
    memo = new int[m][n];
    for (int[] row : memo)
        Arrays.fill(row, -1);

    return dp(grid, m - 1, n - 1);
}


int dp(int[][] grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        return grid[0][0];
    }
    if (i < 0 || j < 0) {
        return Integer.MAX_VALUE;
    }
    // 避免重复计算
    if (memo[i][j] != -1) {
        return memo[i][j];
    }
    // 将计算结果记入备忘录
    memo[i][j] = Math.min(
        dp(grid, i - 1, j),
        dp(grid, i, j - 1)
    ) + grid[i][j];

    return memo[i][j];
}

至此，本题就算是解决了，时间复杂度和空间复杂度都是O(MN)，标准的自顶向下动态规划解法。

有的读者可能问，能不能用自底向上的迭代解法来做这道题呢？完全可以的。

首先，类似刚才的dp函数，我们需要一个二维dp数组，定义如下：

从左上角位置(0, 0)走到位置(i, j)的最小路径和为dp[i][j]。

状态转移方程当然不会变的，dp[i][j]依然取决于dp[i-1][j]和dp[i][j-1]，直接看代码吧：

int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];

        /**** base case ****/
        dp[0][0] = grid[0][0];

        for (int i = 1; i < m; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];

        for (int j = 1; j < n; j++)
            dp[0][j] = dp[0][j - 1] + grid[0][j];        
        /*******************/

        // 状态转移
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }

这个解法的 base case 看起来和递归解法略有不同，但实际上是一样的。

因为状态转移为下面这段代码：

dp[i][j] = Math.min(
    dp[i - 1][j],
    dp[i][j - 1]
) + grid[i][j];

那如果i或者j等于 0 的时候，就会出现索引越界的错误。

所以我们需要提前计算出dp[0][..]和dp[..][0]，然后让i和j的值从 1 开始迭代。

dp[0][..]和dp[..][0]的值怎么算呢？其实很简单，第一行和第一列的路径和只有下面这一种情况嘛：

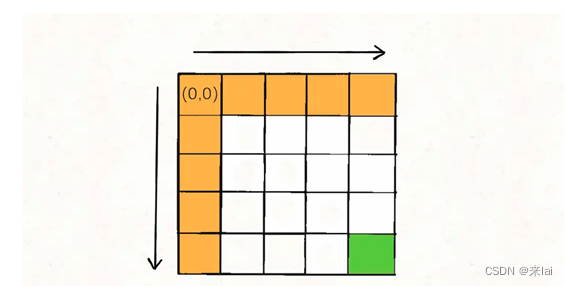
那么按照dp数组的定义，dp[i][0] = sum(grid[0..i][0]), dp[0][j] = sum(grid[0][0..j])，也就是如下代码：

/**** base case ****/
dp[0][0] = grid[0][0];

for (int i = 1; i < m; i++)
    dp[i][0] = dp[i - 1][0] + grid[i][0];

for (int j = 1; j < n; j++)
    dp[0][j] = dp[0][j - 1] + grid[0][j];        
/*******************/

股票问题

**第188题是一个最泛化的形式，其他的问题都是这个形式的简化。**第121题是只进行一次交易，相当于 k = 1；第122题是不限交易次数，相当于 k = +infinity（正无穷）；第123题是只进行 2 次交易，相当于 k = 2；剩下两道也是不限交易次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。

一、穷举框架

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

具体到当前问题，每天都有三种「选择」：买入、卖出、无操作，我们用 buy, sell, rest 表示这三种选择。

但问题是，并不是每天都可以任意选择这三种选择的，因为 sell 必须在 buy 之后，buy 必须在 sell 之后（第一次除外）。那么 rest 操作还应该分两种状态，一种是 buy 之后的 rest（持有了股票），一种是 sell 之后的 rest（没有持有股票）。而且别忘了，我们还有交易次数 k 的限制，就是说你 buy 还只能在 k > 0 的前提下操作。

很复杂对吧，不要怕，我们现在的目的只是穷举，你有再多的状态，老夫要做的就是一把梭全部列举出来。这个问题的「状态」有三个，第一个是天数，第二个是当天允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。

我们用一个三维数组 dp 就可以装下这几种状态的全部组合，用 for 循环就能完成穷举：

dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数，大 K 为最多交易数
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

而且我们可以用自然语言描述出每一个状态的含义，比如说 dp[3][2][1] 的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易。再比如 dp[2] [ 3 ] [0] 的含义：今天是第二天，我现在手上没有持有股票，至今最多进行 3 次交易。很容易理解，对吧？

我们想求的最终答案是 dp[ n - 1 ] [ K] [0]，即最后一天，最多允许 K 次交易，所能获取的最大利润。读者可能问为什么不是 dp[n - 1] [K] [1]？因为 [1] 代表手上还持有股票，[0] 表示手上的股票已经卖出去了，很显然后者得到的利润一定大于前者。

记住如何解释「状态」，一旦你觉得哪里不好理解，把它翻译成自然语言就容易理解了。

二、状态转移框架

现在，我们完成了「状态」的穷举，我们开始思考每种「状态」有哪些「选择」，应该如何更新「状态」。

因为我们的选择是 buy, sell, rest，而这些选择是和「持有状态」相关的，所以只看「持有状态」，可以画个状态转移图。

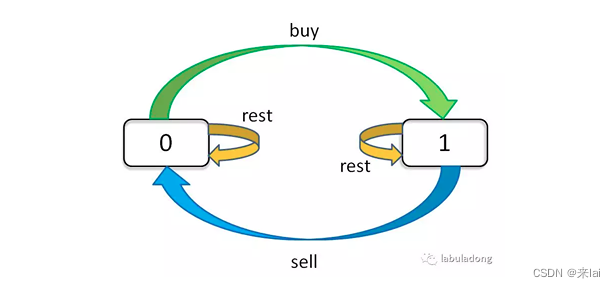
通过这个图可以很清楚地看到，每种状态（0 和 1）是如何转移而来的。根据这个图，我们来写一下状态转移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max(   选择 rest  ,           选择 sell      )

解释：今天我没有持有股票，有两种可能：
要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有；
要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max(   选择 rest  ,           选择 buy         )

解释：今天我持有着股票，有两种可能：
要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票；
要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了。

可能有同学对第二个转移方程中
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
的k-1不理解，我个人的理解是把购买股票看作一次交易的标志，每次购买股票最大交易次数k减一。

当然也可以将出售股票看作一次交易的标志，每次出售股票最大交易次数减一。这种情况下要将第一个转移方程修改为：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k-1][1] + prices[i])

这个解释应该很清楚了，如果 buy，就要从利润中减去 prices[i]，如果 sell，就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。而且注意 k 的限制，我们在选择 buy 的时候，把最大交易数 k 减小了 1，很好理解吧，当然你也可以在 sell 的时候减 1，一样的。

现在，我们已经完成了动态规划中最困难的一步：状态转移方程。**如果之前的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就行了。**不过还差最后一点点，就是定义 base case，即最简单的情况。

dp[-1][k][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释：还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。
dp[i][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。

把上面的状态转移方程总结一下：

base case：
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

读者可能会问，这个数组索引是 -1 怎么编程表示出来呢，负无穷怎么表示呢？这都是细节问题，有很多方法实现。现在整体框架已经完成，下面开始具体化。

三、秒杀题目

第121题，k = 1

直接套状态转移方程，根据 base case，可以做一些化简：

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])
			= max(dp[i-1][1][1], -prices[i])
解释：k = 0 的 base case，所以 dp[i-1][0][0] = 0。

现在发现 k 都是 1，不会改变，即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])

直接翻译成代码：

int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

显然 i = 0 时 dp[i-1] 是不合法的。这是因为我们没有对 i 的 base case 进行处理。那就简单粗暴地处理一下：

for (int i = 0; i < n; i++) {
    if (i - 1 == -1) {
        dp[i][0] = 0;
        // 解释：
        //   dp[i][0] 
        // = max(dp[-1][0], dp[-1][1] + prices[i])
        // = max(0, -infinity + prices[i]) = 0
        dp[i][1] = -prices[i];
        //解释：
        //   dp[i][1] 
        // = max(dp[-1][1], dp[-1][0] - prices[i])
        // = max(-infinity, 0 - prices[i]) 
        // = -prices[i]
        continue;
    }
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

第一题就解决了，但是这样处理 base case 很麻烦，而且注意一下状态转移方程，新状态只和相邻的一个状态有关，其实不用整个 dp 数组，只需要两个变量储存所需的状态就足够了，这样可以把空间复杂度降到 O(1):

// k == 1
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = Math.max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

两种方式都是一样的，不过这种编程方法简洁很多。但是如果没有前面状态转移方程的引导，是肯定看不懂的。后续的题目，我主要写这种空间复杂度 O(1) 的解法。

第122题，k = +infinity

如果 k 为正无穷，那么就可以认为 k 和 k - 1 是一样的。可以这样改写框架：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
            = max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])

我们发现数组中的 k 已经不会改变了，也就是说不需要记录 k 这个状态了：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])

直接翻译代码即可：

int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

第309题，k = +infinity with cooldown（冷冻期）

每次 sell 之后要等一天才能继续交易。只要把这个特点融入上一题的状态转移方程即可：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，而不是 i-1 。

直接翻译成代码即可：

int maxProfit_with_cool(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    int dp_pre_0 = 0; // 代表 dp[i-2][0]
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
        dp_pre_0 = temp;
    }
    return dp_i_0;
}

第714题，k = +infinity with fee （手续费）

每次交易要支付手续费，只要把手续费从利润中减去即可：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释：相当于买入股票的价格升高了。
在第一个式子里减也是一样的，相当于卖出股票的价格减小了。

直接翻译成代码即可：

int maxProfit_with_fee(int[] prices, int fee) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee);
    }
    return dp_i_0;
}

注意：由于dp_i_1初始化为最小的int值，如果在第一个式子即卖出股票中减去fee可能会导致溢出。

dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i] - fee);
dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
可能会导致溢出

第123题，k = 2

k = 2 和前面题目的情况稍微不同，因为上面的情况都和 k 的关系不太大。要么 k 是正无穷，状态转移和 k 没关系了；要么 k = 1，跟 k = 0 这个 base case 挨得近，最后也被消掉了。

这道题 k = 2 和后面要讲的 k 是任意正整数的情况中，对 k 的处理就凸显出来了。我们直接写代码，边写边分析原因。

原始的动态转移方程，没有可化简的地方
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

按照之前的代码，我们可能想当然这样写代码（错误的）：

int k = 2;
int[][][] dp = new int[n][k + 1][2];
for (int i = 0; i < n; i++)
    if (i - 1 == -1) { /* 处理一下 base case*/ }
    dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
    dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];

为什么错误？我这不是照着状态转移方程写的吗？

还记得前面总结的「穷举框架」吗？就在强调必须穷举所有状态。其实我们之前的解法，都在穷举所有状态，只是之前的题目中 k 都被化简掉了，所以没有对 k 的穷举。比如说第一题，k = 1：

这道题由于没有消掉 k 的影响，所以必须要用 for 循环对 k 进行穷举才是正确的：

int max_k = 2;
int n= prices.length;
int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++) {
    for (int k = max_k; k >= 1; k--) {
        if (i - 1 == -1) { 
            /* 处理 base case */
            dp[i][k][0] = 0;
            dp[i][k][1] = -prices[i];
            continue;
        }
        dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
        dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
    }
}
// 穷举了 n × max_k × 2 个状态，正确。
return dp[n - 1][max_k][0];

如果你不理解，可以返回第一点「穷举框架」重新阅读体会一下。

第二种解法：因为这里 k 取值范围比较小，所以也可以不用 for 循环，直接把 k = 1 和 2 的情况手动列举出来也是一样的：

dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], -prices[i])

int maxProfit_k_2(int[] prices) {
    int dp_i10 = 0, dp_i11 = Integer.MIN_VALUE;
    int dp_i20 = 0, dp_i21 = Integer.MIN_VALUE;
    for (int price : prices) {
        dp_i20 = Math.max(dp_i20, dp_i21 + price);
        dp_i21 = Math.max(dp_i21, dp_i10 - price);
        dp_i10 = Math.max(dp_i10, dp_i11 + price);
        dp_i11 = Math.max(dp_i11, -price);
    }
    return dp_i20;
}

有状态转移方程和含义明确的变量名引导，相信你很容易看懂。如我我们想故弄玄虚，可以把上述四个变量换成 a, b, c, d。这样当别人看到你的解法时就会大惊失色，一头雾水，不得不对你肃然起敬。

第188题，k = any integer （任意k）

这题和 k = 2 没啥区别，可以直接套上一题的第一个解法。但是提交之后会出现一个超内存的错误，原来是传入的 k 值可以任意大，导致 dp 数组太大了。现在想想，交易次数 k 最多能有多大呢？

一次交易由买入和卖出构成，至少需要两天。所以说有效的限制次数 k 应该不超过 n/2，如果超过，就没有约束作用了，相当于 k = +infinity。这种情况是之前解决过的。

直接把之前的代码重用：

int maxProfit_k_any(int max_k, int[] prices) {
    int n = prices.length;
    if (max_k > n / 2) 
        return maxProfit_k_inf(prices);

    int[][][] dp = new int[n][max_k + 1][2];
    for (int i = 0; i < n; i++) 
        for (int k = max_k; k >= 1; k--) {
            if (i - 1 == -1) { 
                /* 处理 base case */
                dp[i][k][0] = 0;
                dp[i][k][1] = -prices[i];
                continue;
            }
            dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
            dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);     
        }
    return dp[n - 1][max_k][0];
}

打家劫舍问题

第一道是比较标准的动态规划问题，而第二道融入了环形数组的条件，第三道更绝，让盗贼在二叉树上打劫

198.打家劫舍I

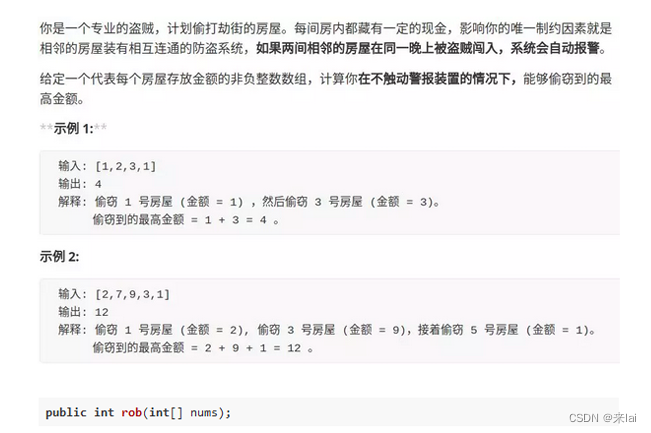
解决动态规划问题就是找「状态」和「选择」，仅此而已。

假想你就是这个专业强盗，从左到右走过这一排房子，在每间房子前都有两种选择：抢或者不抢。

如果你抢了这间房子，那么你肯定不能抢相邻的下一间房子了，只能从下下间房子开始做选择。

如果你不抢这间房子，那么你可以走到下一间房子前，继续做选择。

当你走过了最后一间房子后，你就没得抢了，能抢到的钱显然是 0（base case）。

以上的逻辑很简单吧，其实已经明确了「状态」和「选择」：你面前房子的索引就是状态，抢和不抢就是选择。

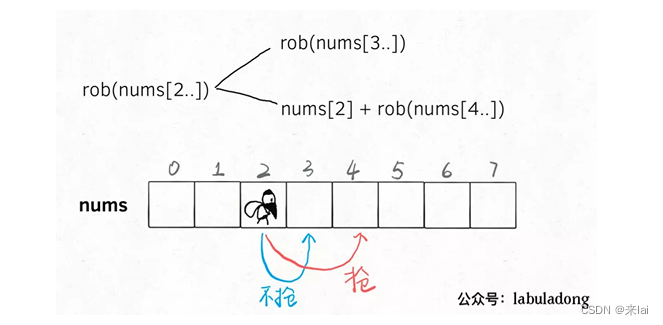
在两个选择中，每次都选更大的结果，最后得到的就是最多能抢到的 money：

// 主函数
public int rob(int[] nums) {
    return dp(nums, 0);
}
// 返回 nums[start..] 能抢到的最大值
private int dp(int[] nums, int start) {
    if (start >= nums.length) {
        return 0;
    }

    int res = Math.max(
            // 不抢，去下家
            dp(nums, start + 1), 
            // 抢，去下下家
            nums[start] + dp(nums, start + 2)
        );
    return res;
}

明确了状态转移，就可以发现对于同一start位置，是存在重叠子问题的，比如下图：

盗贼有多种选择可以走到这个位置，如果每次到这都进入递归，岂不是浪费时间？所以说存在重叠子问题，可以用备忘录进行优化：

private int[] memo;
// 主函数
public int rob(int[] nums) {
    // 初始化备忘录
    memo = new int[nums.length];
    Arrays.fill(memo, -1);
    // 强盗从第 0 间房子开始抢劫
    return dp(nums, 0);
}

// 返回 dp[start..] 能抢到的最大值
private int dp(int[] nums, int start) {
    if (start >= nums.length) {
        return 0;
    }
    // 避免重复计算
    if (memo[start] != -1) return memo[start];

    int res = Math.max(dp(nums, start + 1), 
                    nums[start] + dp(nums, start + 2));
    // 记入备忘录
    memo[start] = res;
    return res;
}

这就是自顶向下的动态规划解法，我们也可以略作修改，写出自底向上的解法：

 int rob(int[] nums) {
    int n = nums.length;
    // dp[i] = x 表示：
    // 从第 i 间房子开始抢劫，最多能抢到的钱为 x
    // base case: dp[n] = 0
    int[] dp = new int[n + 2];
    for (int i = n - 1; i >= 0; i--) {
        dp[i] = Math.max(dp[i + 1], nums[i] + dp[i + 2]);
    }
    return dp[0];
}

我们又发现状态转移只和dp[i]最近的两个状态有关，所以可以进一步优化，将空间复杂度降低到 O(1)。

int rob(int[] nums) {
    int n = nums.length;
    // 记录 dp[i+1] 和 dp[i+2]
    int dp_i_1 = 0, dp_i_2 = 0;
    // 记录 dp[i]
    int dp_i = 0; 
    for (int i = n - 1; i >= 0; i--) {
        dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i;
}

213.打家劫舍II

这道题目和第一道描述基本一样，强盗依然不能抢劫相邻的房子，输入依然是一个数组，但是告诉你这些房子不是一排，而是围成了一个圈。

也就是说，现在第一间房子和最后一间房子也相当于是相邻的，不能同时抢。比如说输入数组nums=[2,3,2]，算法返回的结果应该是 3 而不是 4，因为开头和结尾不能同时被抢。

这个约束条件看起来应该不难解决，我们前文 单调栈 Monotonic Stack 的使用 说过一种解决环形数组的方案，那么在这个问题上怎么处理呢？

首先，首尾房间不能同时被抢，那么只可能有三种不同情况：要么都不被抢；要么第一间房子被抢最后一间不抢；要么最后一间房子被抢第一间不抢。

那就简单了啊，这三种情况，哪种的结果最大，就是最终答案呗！不过，其实我们不需要比较三种情况，**只要比较情况二和情况三就行了，**因为这两种情况对于房子的选择余地比情况一大呀，房子里的钱数都是非负数，所以选择余地大，最优决策结果肯定不会小。

所以只需对之前的解法稍作修改即可：

public int rob(int[] nums) {
    int n = nums.length;
    if (n == 1) return nums[0];
    return Math.max(robRange(nums, 0, n - 2), 
                    robRange(nums, 1, n - 1));
}

// 仅计算闭区间 [start,end] 的最优结果
int robRange(int[] nums, int start, int end) {
    int n = nums.length;
    int dp_i_1 = 0, dp_i_2 = 0;
    int dp_i = 0;
    for (int i = end; i >= start; i--) {
        dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i;
}

337.打家劫舍III

第三题又想法设法地变花样了，此强盗发现现在面对的房子不是一排，不是一圈，而是一棵二叉树！房子在二叉树的节点上，相连的两个房子不能同时被抢劫：

整体的思路完全没变，还是做抢或者不抢的选择，取收益较大的选择。甚至我们可以直接按这个套路写出代码：

Map<TreeNode, Integer> memo = new HashMap<>();
public int rob(TreeNode root) {
    if (root == null) return 0;
    // 利用备忘录消除重叠子问题
    if (memo.containsKey(root)) 
        return memo.get(root);
    // 抢，然后去下下家
    int do_it = root.val
        + (root.left == null ? 
            0 : rob(root.left.left) + rob(root.left.right))
        + (root.right == null ? 
            0 : rob(root.right.left) + rob(root.right.right));
    // 不抢，然后去下家
    int not_do = rob(root.left) + rob(root.right);

    int res = Math.max(do_it, not_do);
    memo.put(root, res);
    return res;
}

这道题就解决了，时间复杂度 O(N)，N为数的节点数。

但是这道题让我觉得巧妙的点在于，还有更漂亮的解法。比如下面是我在评论区看到的一个解法：

int rob(TreeNode root) {
    int[] res = dp(root);
    return Math.max(res[0], res[1]);
}

/* 返回一个大小为 2 的数组 arr
arr[0] 表示不抢 root 的话，得到的最大钱数
arr[1] 表示抢 root 的话，得到的最大钱数 */
int[] dp(TreeNode root) {
    if (root == null)
        return new int[]{0, 0};
    int[] left = dp(root.left);
    int[] right = dp(root.right);
    // 抢，下家就不能抢了
    int rob = root.val + left[0] + right[0];
    // 不抢，下家可抢可不抢，取决于收益大小
    int not_rob = Math.max(left[0], left[1])
                + Math.max(right[0], right[1]);

    return new int[]{not_rob, rob};
}

时间复杂度 O(N)，空间复杂度只有递归函数堆栈所需的空间，不需要备忘录的额外空间。

你看他和我们的思路不一样，修改了递归函数的定义，略微修改了思路，使得逻辑自洽，依然得到了正确的答案，而且代码更漂亮。这就是我们前文 动态规划：不同的定义产生不同的解法 所说过的动态规划问题的一个特性。

10 . 正则表达式匹配

​