1 一些必须的库
关于如何在ripser中使用稀释矩阵,一些必须的库如下:
import numpy as np
import matplotlib.pyplot as plt
import tadasets
from sklearn import datasets
from sklearn.metrics.pairwise import pairwise_distances
from scipy import sparse
from ripser import ripser
from persim import plot_diagrams
2 测试数据
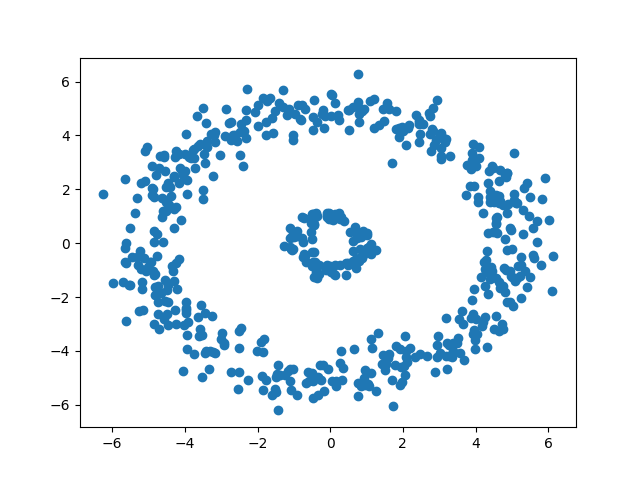
测试数据包含两个噪声圆:
data = np.concatenate([
tadasets.dsphere(n=500, d=1, r=5, noise=0.5),
tadasets.dsphere(n=100, d=1, r=1, noise=0.2)
])
plt.scatter(data[:, 0], data[:, 1])
plt.show()
输出如下:
3 稀疏距离矩阵
使用稀疏距离矩阵与否的计算结果对比:
def makeSparseDM(X, thresh):
N = X.shape[0]
D = pairwise_distances(X, metric='euclidean')
[I, J] = np.meshgrid(np.arange(N), np.arange(N))
I = I[D <= thresh]
J = J[D <= thresh]
V = D[D <= thresh]
return sparse.coo_matrix((V, (I, J)), shape=(N, N)).tocsr()
thresh = 1.5
results0 = ripser(data, thresh=thresh, maxdim=1)
D = makeSparseDM(data, thresh)
results1 = ripser(D, distance_matrix=True)
print("%i edges added in the dense filtration" % results0['num_edges'])
print("%i edges added in the sparse filtration" % results1['num_edges'])
输出如下:
13217 edges added in the dense filtration
13217 edges added in the sparse filtration
4 持续同伦图
plt.figure(figsize=(12, 4))
plt.subplot(131)
plt.scatter(data[:, 0], data[:, 1])
plt.title("Point Cloud")
plt.subplot(132)
plot_diagrams(results0['dgms'], show=False)
plt.title("Dense Filtration")
plt.subplot(133)
plt.title("Sparse Filtration")
plot_diagrams(results1['dgms'], show=False)
plt.tight_layout()
plt.show()
输出如下,可以发现两者的结果几乎是一样的:
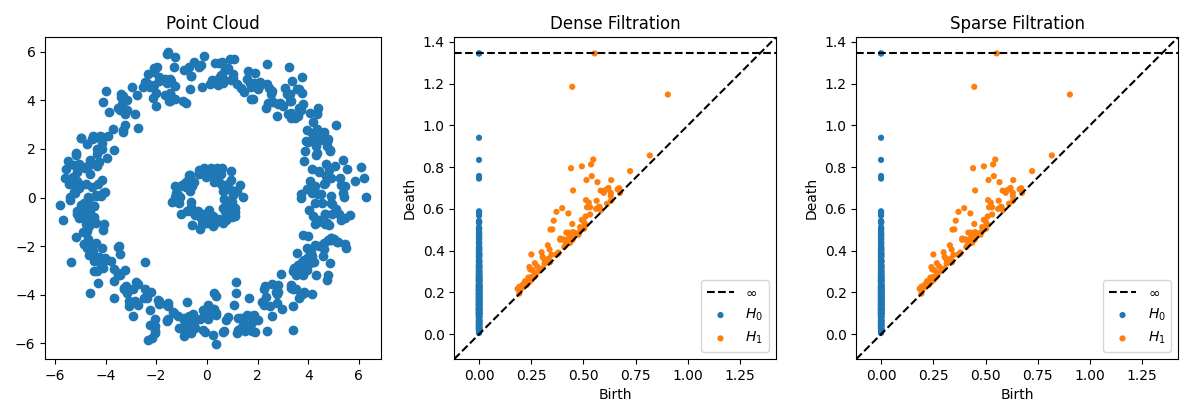





 文章介绍了如何在Python环境中利用ripser库处理稀疏距离矩阵进行持续同伦图的构建。通过测试数据(包含两个噪声圆的点集),对比了使用稀疏距离矩阵与非稀疏矩阵在计算结果上的差异,结果显示两者几乎一致。最后展示了密集和稀疏过滤器生成的持续同伦图。
文章介绍了如何在Python环境中利用ripser库处理稀疏距离矩阵进行持续同伦图的构建。通过测试数据(包含两个噪声圆的点集),对比了使用稀疏距离矩阵与非稀疏矩阵在计算结果上的差异,结果显示两者几乎一致。最后展示了密集和稀疏过滤器生成的持续同伦图。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








