算法-模板

一、递归

1.思维要点

1. 不要人肉递归
2. 找到最近最简方法，将其拆解成可重复解决的问题（找重复子问题）
3. 善于利用数学归纳法思维

---

2.递归模板

1. 递归终止条件
2. 处理当前层逻辑
3. 下探到下一层
4. 清理当前层（可省略）

// Java
public void recur(int level, int param) { 
  // terminator 
  if (level > MAX_LEVEL) { 
    // process result 
    return; 
  }
  // process current logic 
  process(level, param); 
  // drill down 
  recur( level: level + 1, newParam); 
  // restore current status 
 
}

递归代码模板

---

二、分治

1.特点

• 本质是递归，找重复性。分解问题，再组合每个子问题的结果。
• 分治的难点在于如何拆分以及如何合并子结果。
• 和递归一样，当前层就考虑当前层的逻辑，不要下探或者太多，因为人脑不擅长人肉递归。

---

2.分治模板

1. 分治终止条件
2. 处理当前层逻辑，分解子问题
3. 下探到下一层解决子问题
4. 组装子问题
5. 清理当前层（可省略）

# Python
def divide_conquer(problem, param1, param2, ...): 
  # recursion terminator 
  if problem is None: 
	print_result 
	return 

  # prepare data 
  data = prepare_data(problem) 
  subproblems = split_problem(problem, data) 

  # conquer subproblems 
  subresult1 = self.divide_conquer(subproblems[0], p1, ...) 
  subresult2 = self.divide_conquer(subproblems[1], p1, ...) 
  subresult3 = self.divide_conquer(subproblems[2], p1, ...) 
  …

  # process and generate the final result 
  result = process_result(subresult1, subresult2, subresult3, …)
	
  # revert the current level states

分治代码模板

---

三、回溯

1.特点

• 通常用递归实现
• 采用试错的思想，不断尝试下探，直到找到结果，所以时间复杂度相对高
• 能找到一个可能存在的正确解
• 如果尝试了所有的下探路径，都没有则说明该问题没有答案。
• 最坏的情况下导致时间复杂度为指数时间

2.回溯模板

常见的题目通常是给一个数组数据或者字符串，然后求其所有组成。

1. 创建回溯体（常见参数：目标参数、递归层数、中间处理集合、返回结果集合）
2. 回溯终止条件（处理结果）
3. 处理当前层逻辑
4. 递归进入下一层
5. 回溯清理当前层

Class Solation{
	public List<List<Integer>> backtrack(int[] a)
	{
	 List<List<Integer>> list = new ArrayList<>();
	 //Arrays.sort(a);//当a中存在重复值。而重复值不能使用的时候。就要进行排序。对使用过的重复值不再使用
	 backTrackTemp(list, new ArrayList<>(), a, .....)//其中的"...."表示其他限定条件(根据条件限定而存在与否)
	 return list;
}
//回溯过程
private static void backTrackTemp(List<List<Object>> list, Arraylist<Integer> tempList, int[] a,....)
{
	//终止条件，也就是一次结果或者不符合条件
	if(false)//false代表条件不符合
		return false;
	if(true)//当符合需要的结果
		list.add(new ArrayList(tempList))//注意这里要重新创建，因为tempList是一个对象，改变的话，会改变结果值。所以重新创建
	//对每个值进行回溯
	for(int i = start; i < a.length; i++)
	{
		if(true)//存在某个限定条件的，比如出现重复值,跳过(根据条件限定而存在与否)
			continue;
		mask(used(i));//将i标记为已使用(根据条件限定而存在与否)
		backTrackTemp(list, tempList, a, i+1)//此处的i+1也可以根据实际情况判断题目中的数字是否可以重复使用
		unmask(used(i));//回溯完要记得取消掉
		tempList.remove(tempList.size() - 1);//回溯回父节点.寻找下一个节点
	}
}

}

四、贪心

1.特点

• 贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。
• 一旦一个问题可以通过贪心法来解决，那么贪心法一般是解决这个问题的最好办法。
• 贪心法可以解决一些最优化问题，然而对于工程和生活中的问题，贪心法一般不能得到我们所要求的答案。

2.对比动态规划、回溯

• 贪心：当下做出局部最优判断，不能回退
• 回溯：能够回溯，但是偏暴力搜索
• 动态规划：最优判断+回溯（保存之前的运算结果，在适当的时候进行回退）

---

五、动态规划

特点

• 动态规划和递归或者分治没有根本上的区别（关键看有无最优的子结构）
• 共性：找重复的子问题
• 差异：具有最优子结构，中途可以淘汰次优解

步骤

• 找出最优子结构性质，并刻画其结构特征
• 递归地定义最优值
• 以自底向上的方式计算出最优值
• 根据计算最优值得到的信息，构造最优解。

六、搜索遍历

1.深度优先遍历

1.1遍历顺序

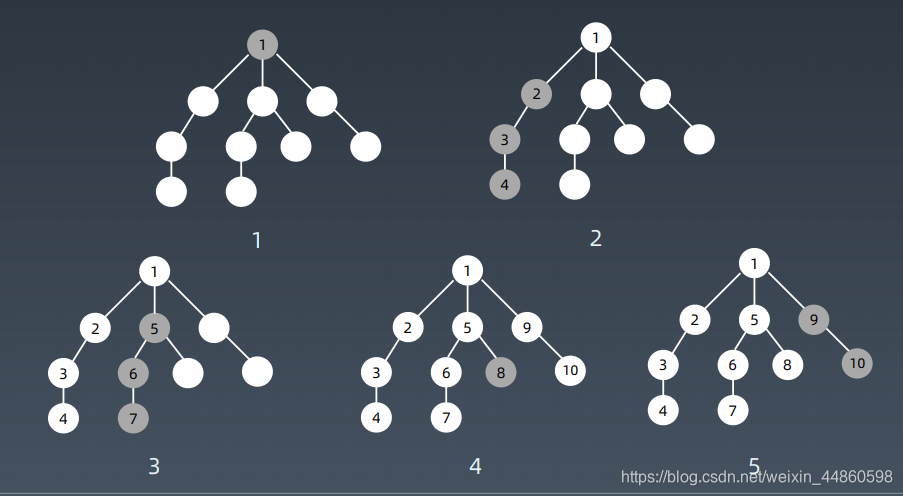
1.2代码模板（递归方式）

1. 判断当前节点是否已遍历
2. 遍历当前节点
3. 处理当前层逻辑
4. 递归下探一层（遍历子节点）

visited = set() 

def dfs(node, visited):
    if node in visited: # terminator
    	# already visited 
    	return 

	visited.add(node) 

	# process current node here. 
	...
	for next_node in node.children(): 
		if next_node not in visited: 
			dfs(next_node, visited)

1.3代码模板（迭代方式）

1. 判断当前节点是否已遍历
2. 创建栈，并把当前节点加入栈中
3. 如果栈不为空，从栈顶取出当前节点
4. 遍历当前节点
5. 处理当前层逻辑
6. 把子节点加入栈中

def DFS(self, tree): 

	if tree.root is None: 
		return [] 

	visited, stack = [], [tree.root]

	while stack: 
		node = stack.pop() 
		visited.add(node)

		process (node) 
		nodes = generate_related_nodes(node) 
		stack.push(nodes) 

	# other processing work 

深度优先遍历代码模板

---

2.广度优先遍历

2.1遍历顺序

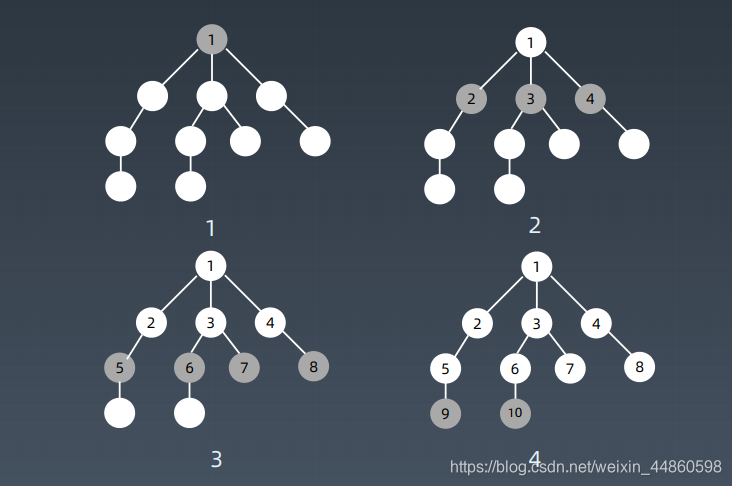
2.2代码模板（队列实现）

1. 判断当前节点是否已遍历
2. 创建队列，并把当前节点加入队列
3. 如果队列不为空，从队列中取出当前节点
4. 遍历当前节点
5. 处理当前层逻辑
6. 把把子节点放入队列中

def BFS(graph, start, end):
    visited = set()
	queue = [] 
	queue.append([start]) 
	while queue: 
		node = queue.pop() 
		visited.add(node)
		process(node) 
		nodes = generate_related_nodes(node) 
		queue.push(nodes)
	# other processing work 

广度优先遍历代码模板

---

3.深度优先遍历和广度优先遍历对比

3.1相同点

• 每个节点都要访问一次
• 每个节点仅仅要访问一次
• 对于节点的访问顺序不限

3.2不同顺序

---

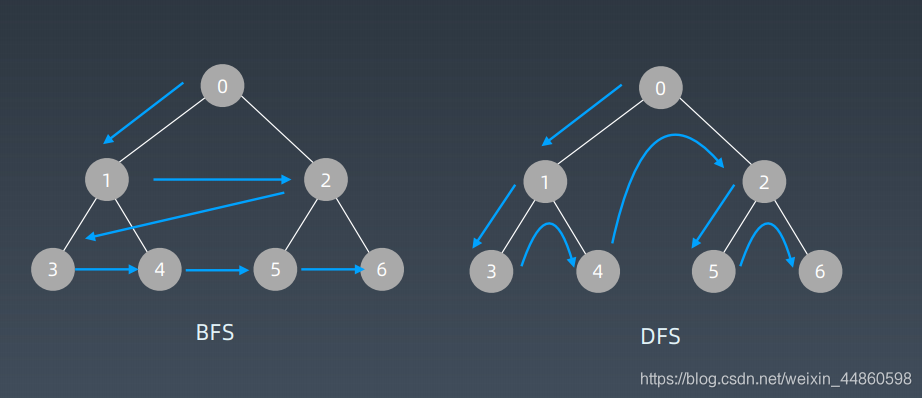
4.二分查找

4.1特点

• 目标单调性（单调递增或者递减）
• 存在上下界
• 能够通过索引访问
• 二分查找每次查找都减掉一半的元素，类似搜索二叉树的遍历，只不过它是通过数组实现。

4.2二分查找模板

1. 定义查找的上下界（左右边界）
2. 当满足边界条件（左边界小于等于右边界）
3. 得到中间边界
4. 如果查到目标值，返回
5. 如果查到的值大于目标值，往左半区继续查找
6. 如果查到的值小于目标值，往右半区继续查找

public int binarySearch(int[] array, int target) {
    int left = 0, right = array.length - 1, mid;
    while (left <= right) {
        mid = (right - left) / 2 + left;

        if (array[mid] == target) {
            return mid;
        } else if (array[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    return -1;
}

二分查找模板

---