【GVN】Kildall算法的推导

本文的例子来自RKS算法的那篇文章《Detecting Equalities of Variables: Combining
Efficiency with Precision》，只是进行了部分现代化和本土化。
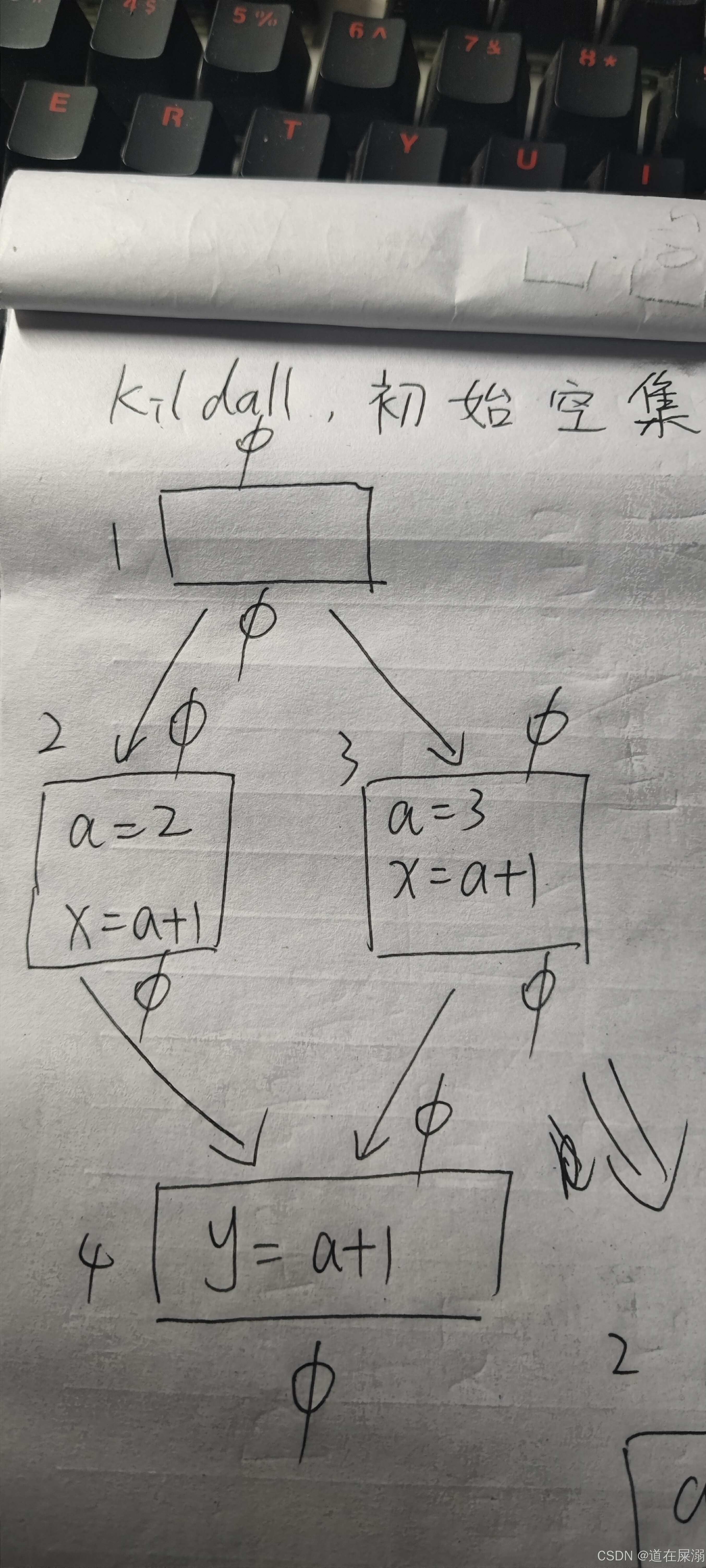首先，对于非循环的情况，Kildall会将所有节点的进入和离开状态都设为空集，进行悲观推导。

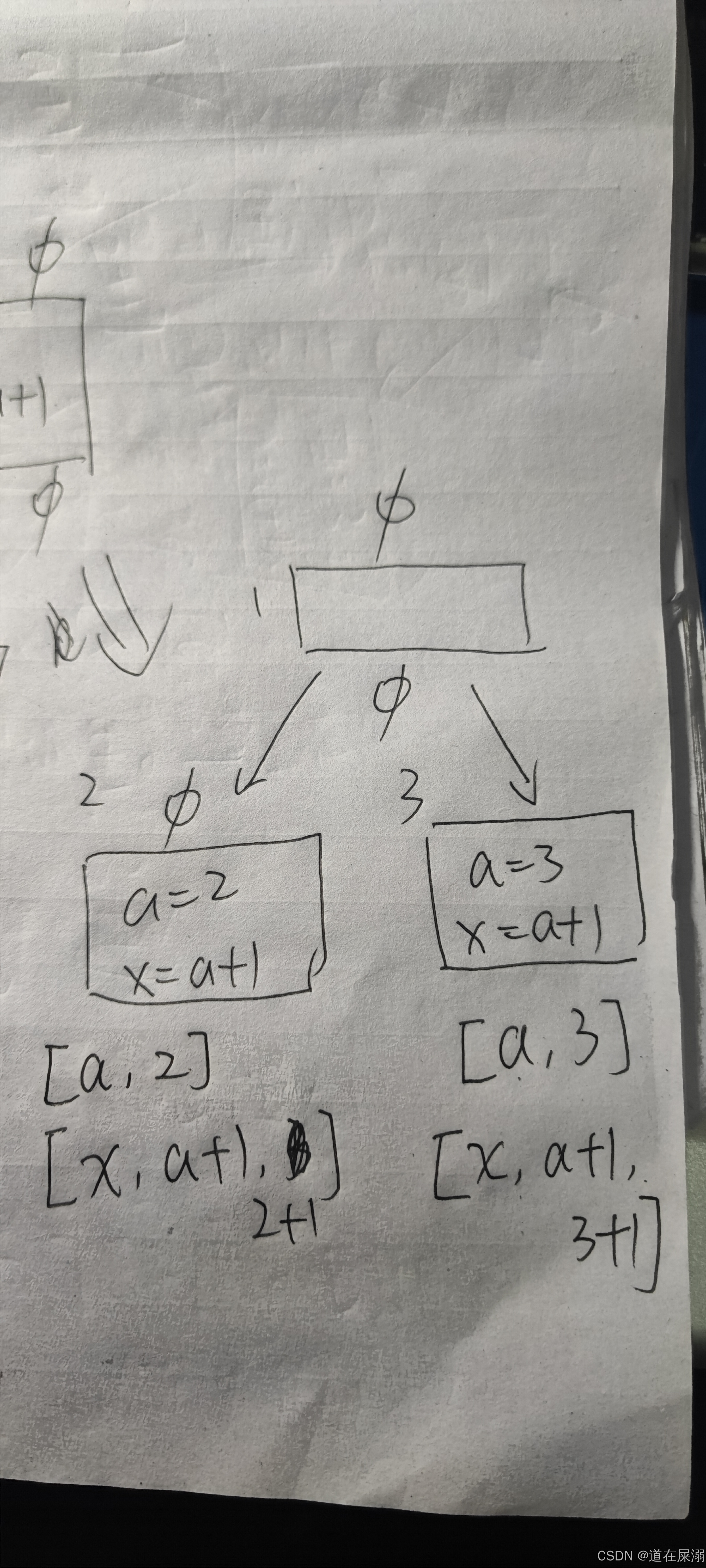
推导完得到的2号基本块和3号基本块的出口状态对应的集合如上所示，其中2+1并不写为3（如果 要进行常量折叠的话可以写为3）。
Kildall算法的meet操作是intersection，所以得到的结果如下：

对于循环的情况，除了开始节点的入口，所有节点的集合都要设为T，进行乐观推理。

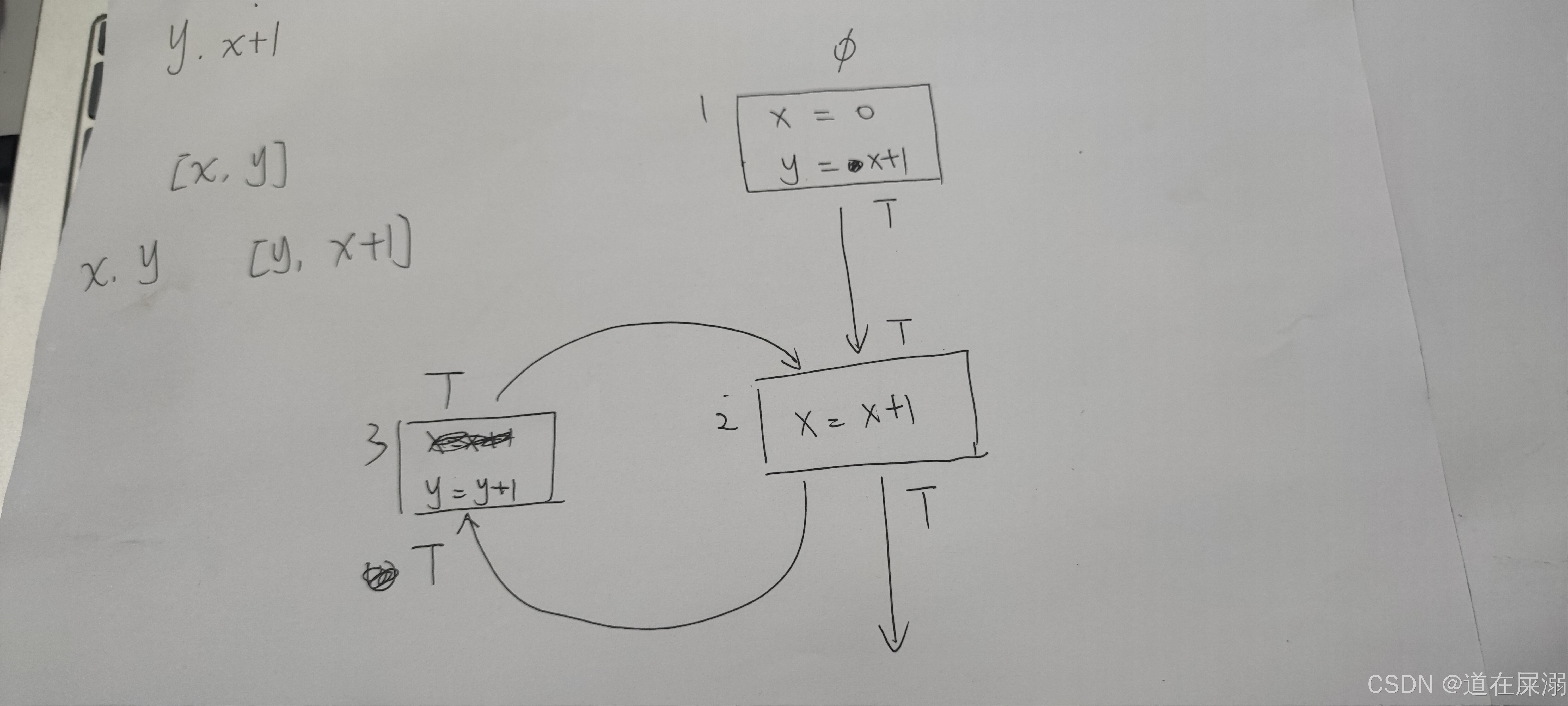
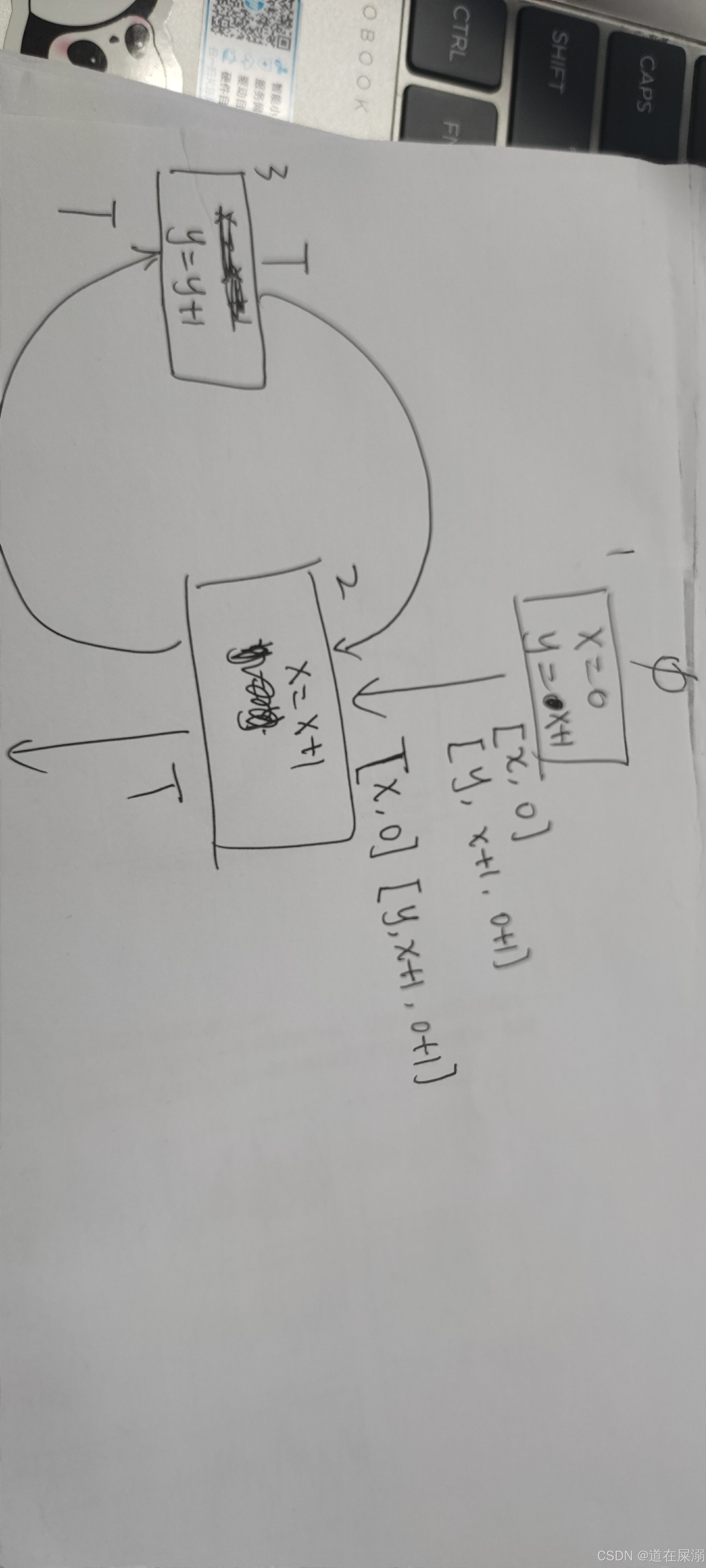
对于循环的情况，首先会进行循环入口节点的状态计算，此时因为是T，所以可以顺利传递进去。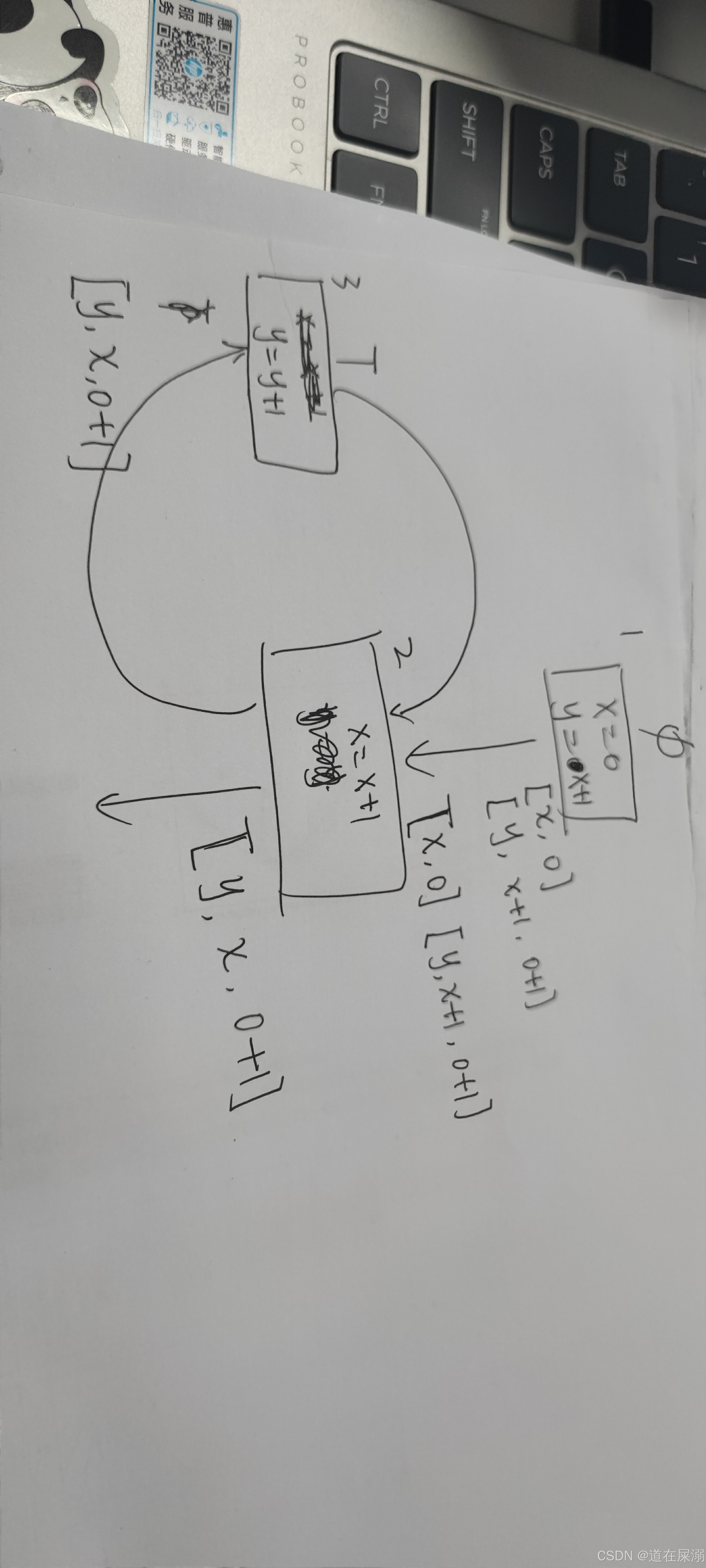一轮传递过后，可能还需要重新传递，因为一些循环改变量会影响intersection的结果。


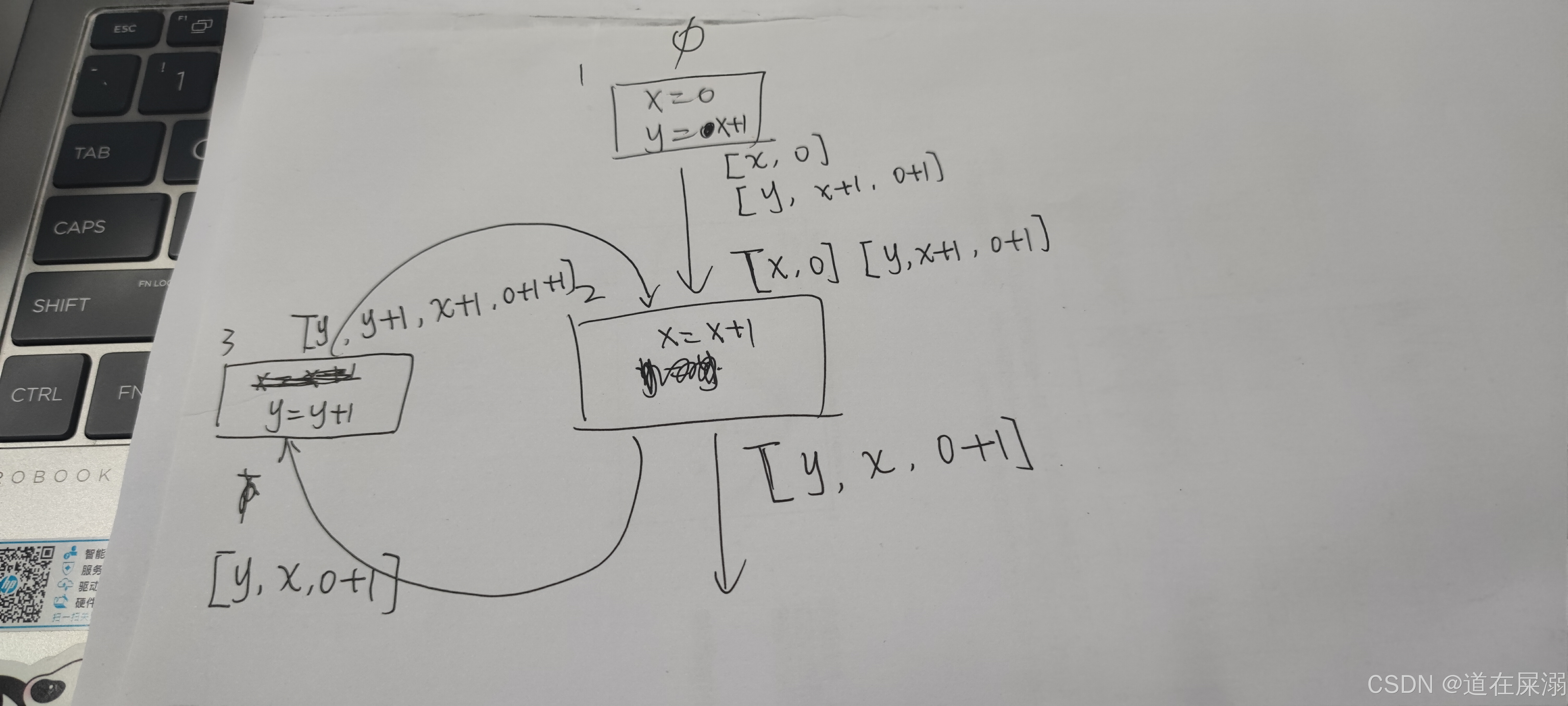
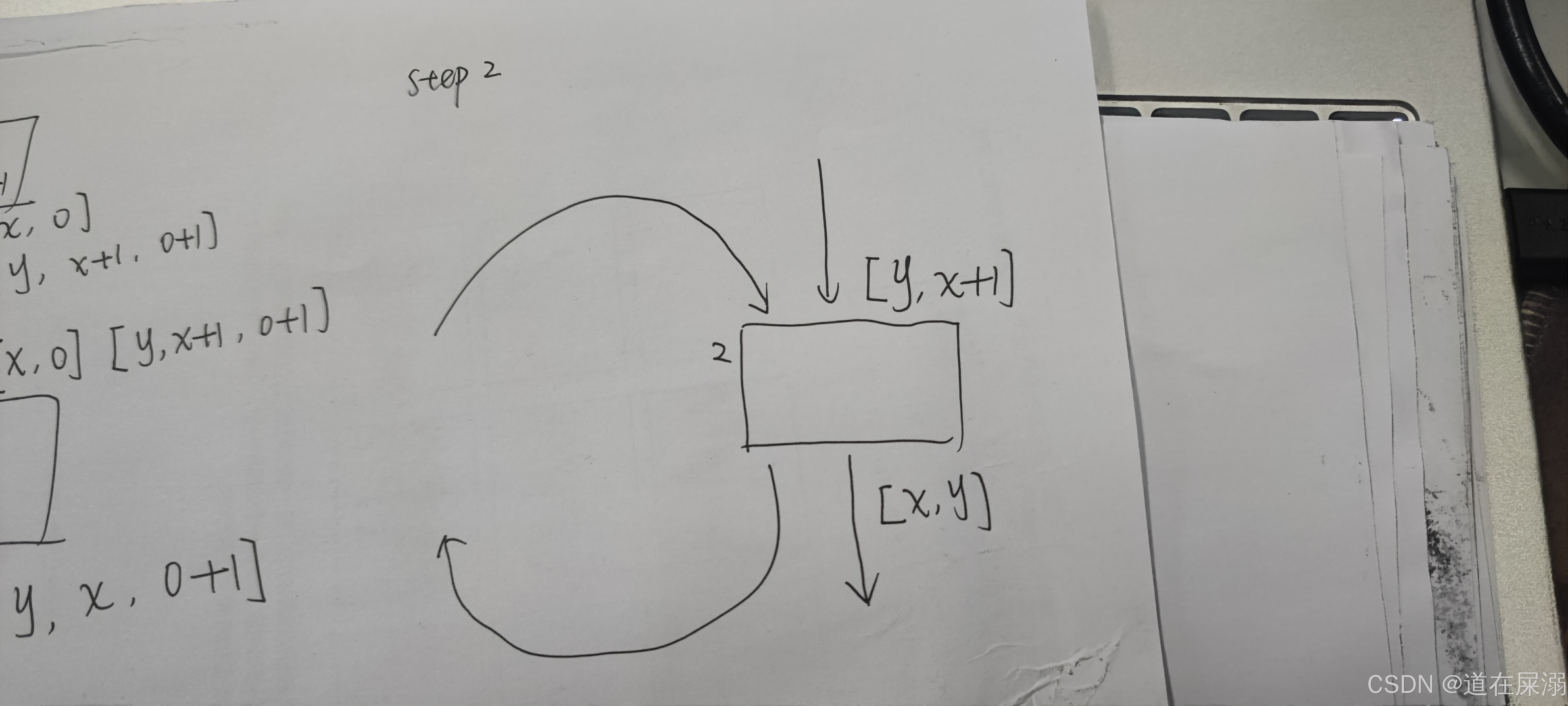
上图展示了第二轮循环的情况，此时如果哪个节点的入口状态不发生改变说明循环结构达到了fixed point。