一起啃书——MIMO-OFDM无线通信技术
文章目录
SISO 信道模型
前言
为了建立一个在某种特定环境下准确的信道模型,我们必须充分掌握有关反射体特点的知识,包括它们的位置和运动,以及在特定时间内反射信号的功率。在实际中,像这样完全的特性描述是不可能实现的,所以我们求助于某种特定的信道模型,而这种特定的信道模型可以表示某种给定环境下典型的或平均的信道情况。
室内信道模型
终端在建筑内的移动速度极低,可以认为信道是趋于静止的。
当信号强度在一个符号周期内随时间的波动程度较小时,可以认为信道环境是静态的。
室内信道模型以解决静态或者准静态信道环境下的多径时延问题。
室内信道模型:2-径模型和指数模型
2-径模型
模型中其设定为有两条射线,一条是具有零时延(
τ
0
=
0
\tau_0 = 0
τ0=0)的直射路径,另一条是时延(
τ
0
>
0
\tau_0 > 0
τ0>0)的反射路径,两条路径的功率相同[如图 2.1(a)所示的 PDP]。模型中最大过量时延为
τ
m
=
τ
1
\tau_m = \tau_1
τm=τ1,而平均过量时延可由
τ
ˉ
=
τ
1
/
2
\bar{\tau} = \tau_1 / 2
τˉ=τ1/2来计算。在这种情况下,RMS 时延与平均过量时延相等,即
τ
ˉ
=
σ
τ
=
τ
1
/
2
\bar{\tau} = \sigma_\tau=\tau_1 / 2
τˉ=στ=τ1/2。换句话说,第二条路径的时延是决定这一特殊模型的唯一参数。由于相对简便,2-径模型在实际中的应用较为广泛。但它不够精确,因为在实际应用中第二条路径的幅度通常要比第一条路径小得多。只有第一条路径有明显损耗时,才可以采用2-径模型。

指数模型
在指数模型中,信道的平均功率随着信道的时延按指数规律递减:
P
(
τ
)
=
1
τ
d
e
−
τ
/
τ
d
P(\tau) = \frac{1}{\tau_d} e^{-\tau/\tau_d}
P(τ)=τd1e−τ/τd
- τ d \tau_d τd:衰减时间常数(唯一参数)
-
τ
\tau
τ:过量时延(相对于第一条路径)
在指数信道模型中,平均过量时延和RMS时延扩展相等,即 τ ‾ = σ τ = τ d \overline{\tau} = \sigma_{\tau} = \tau_d \quad τ=στ=τd。此外,最大过量时延为
τ m = − τ d ln A \tau_m = -\tau_d \ln A τm=−τdlnA
PDP总功率:
P total = ∑ p = 0 p max P ( p ) = 1 σ τ ⋅ 1 − e − ( p max + 1 ) T s / σ τ 1 − e − T s / σ τ P_{\text{total}} = \sum_{p=0}^{p_{\text{max}}} P(p) = \frac{1}{\sigma_\tau} \cdot \frac{1 - e^{-(p_{\text{max}}+1)T_s/\sigma_\tau}}{1 - e^{-T_s/\sigma_\tau}} Ptotal=p=0∑pmaxP(p)=στ1⋅1−e−Ts/στ1−e−(pmax+1)Ts/στ
P ( p ) = P ( 0 ) e − p T s / σ τ P(p) = P(0)e^{-pT_s/\sigma_\tau} P(p)=P(0)e−pTs/στ
归一化:
P ( 0 ) = 1 P total ⋅ σ τ P(0) = \frac{1}{P_{\text{total}} \cdot \sigma_\tau} P(0)=Ptotal⋅στ1

Saleh-Valenzuela信道模型
通过对室内信道的大量测量,发现时延分布中存在多簇现象,而且每一簇中又有多条射线。图中显示了具有多簇的S-V信道模型,其中每一簇对应一组射线。每一以及每一内射线的到达时间都服从泊松过程。

f
T
m
(
T
m
∣
T
m
−
1
)
=
λ
e
−
λ
(
T
m
−
T
m
−
1
)
,
m
=
1
,
2
,
.
.
.
(2.10)
f_{T_m}(T_m | T_{m-1}) = \lambda e^{-\lambda (T_m - T_{m-1})}, \quad m=1,2,... \tag{2.10}
fTm(Tm∣Tm−1)=λe−λ(Tm−Tm−1),m=1,2,...(2.10)
f
τ
r
,
m
(
τ
r
,
m
∣
τ
r
−
1
,
m
)
=
μ
e
−
μ
(
τ
r
,
m
−
τ
r
−
1
,
m
)
,
r
=
1
,
2
,
.
.
.
(2.11)
f_{\tau_{r,m}}(\tau_{r,m} | \tau_{r-1,m}) = \mu e^{-\mu (\tau_{r,m} - \tau_{r-1,m})}, \quad r=1,2,... \tag{2.11}
fτr,m(τr,m∣τr−1,m)=μe−μ(τr,m−τr−1,m),r=1,2,...(2.11)
| 符号 | 物理意义 | 典型值 |
|---|---|---|
| λ \lambda λ | 簇到达率 | 0.1-1/ns |
| μ \mu μ | 射线到达率 | 1-10/ns |
| T m T_m Tm | 第 m m m簇到达时间 | - |
| τ r , m \tau_{r,m} τr,m | 第 m m m簇第 r r r射线相对时延 | - |
信道冲激响应
h
(
t
)
=
∑
m
=
0
∞
∑
r
=
0
∞
β
r
,
m
e
j
θ
r
,
m
δ
(
t
−
T
m
−
τ
r
,
m
)
(2.12)
h(t) = \sum_{m=0}^{\infty} \sum_{r=0}^{\infty} \beta_{r,m} e^{j\theta_{r,m}} \delta(t - T_m - \tau_{r,m}) \tag{2.12}
h(t)=m=0∑∞r=0∑∞βr,mejθr,mδ(t−Tm−τr,m)(2.12)
PDF
f
β
r
,
m
(
β
)
=
2
β
β
r
,
m
2
‾
e
−
β
2
/
β
r
,
m
2
‾
(2.13)
f_{\beta_{r,m}}(\beta) = \frac{2\beta}{\overline{\beta_{r,m}^2}} e^{-\beta^2 / \overline{\beta_{r,m}^2}} \tag{2.13}
fβr,m(β)=βr,m22βe−β2/βr,m2(2.13)
各路径平均功率服从双指数衰减规律:
β
r
,
m
2
=
β
0
,
0
2
e
−
T
m
/
Γ
e
−
τ
r
,
m
/
γ
(2.14)
\beta_{r,m}^2 = \beta_{0,0}^2 e^{-T_m / \Gamma} e^{-\tau_{r,m}/\gamma} \tag{2.14}
βr,m2=β0,02e−Tm/Γe−τr,m/γ(2.14)
| 符号 | 物理意义 | 典型值范围 | 测量方法 |
|---|---|---|---|
| β 0 , 0 2 \beta_{0,0}^2 β0,02 | 第一路径参考功率 | 归一化为1 | 信道探测 |
| Γ \Gamma Γ | 簇间衰减常数 | 30-100 ns | PDP拟合 |
| γ \gamma γ | 簇内衰减常数 | 5-20 ns | 高分辨率测量 |
引入长期衰落因子
X
X
X:
h
(
t
)
=
X
∑
m
=
0
M
∑
r
=
0
R
β
r
,
m
e
j
θ
r
,
m
δ
(
t
−
T
m
−
τ
r
,
m
)
(2.15)
h(t) = X \sum_{m=0}^{M} \sum_{r=0}^{R} \beta_{r,m} e^{j\theta_{r,m}} \delta(t - T_m - \tau_{r,m}) \tag{2.15}
h(t)=Xm=0∑Mr=0∑Rβr,mejθr,mδ(t−Tm−τr,m)(2.15)
- X 为 20 log 10 ( X ) ∼ N ( 0 , σ x 2 ) X 为20\log_{10}(X) \sim \mathcal{N}(0, \sigma_x^2) X为20log10(X)∼N(0,σx2)
- σ x \sigma_x σx典型值:3-8 dB(室内环境)
室外信道模型
与室内信道的静态或准静态的特点相反,室外信道受终端移动速度的影响,其典型特点是信道增益随时间的变化而变化。室外信道的特点主要由控制信道增益随时间变化的多普勒谱来描述,可以通过滤波后的高斯白噪声(Filtered White Gaussian Noise,FWGN)模型实现不同类型的多普勒谱。
FWGN信道模型
Clarke/Gans 模型
Clarke/Gans 模型是在以下假设条件下推导得到的:移动台周围的散射分量是均匀分布的,且每一分量的功率都相等。在每个分支中,首先在频域产生一个复高斯噪声;然后通过一个多普勒滤波器,这样频域分量就符合多普勒频移;最后将这个经过多普勒频移后的高斯噪声通过 IFFT模块变换为时域信号。由于IFFT模块的输出必须是实信号,所以IFFT模块的输入必须是共轭对称的。将输出的虚部和实部加起来,可以构建一个复信道增益,从而产生一个幅度服从瑞利分布的信道。


改进的频域 FWGN 模型


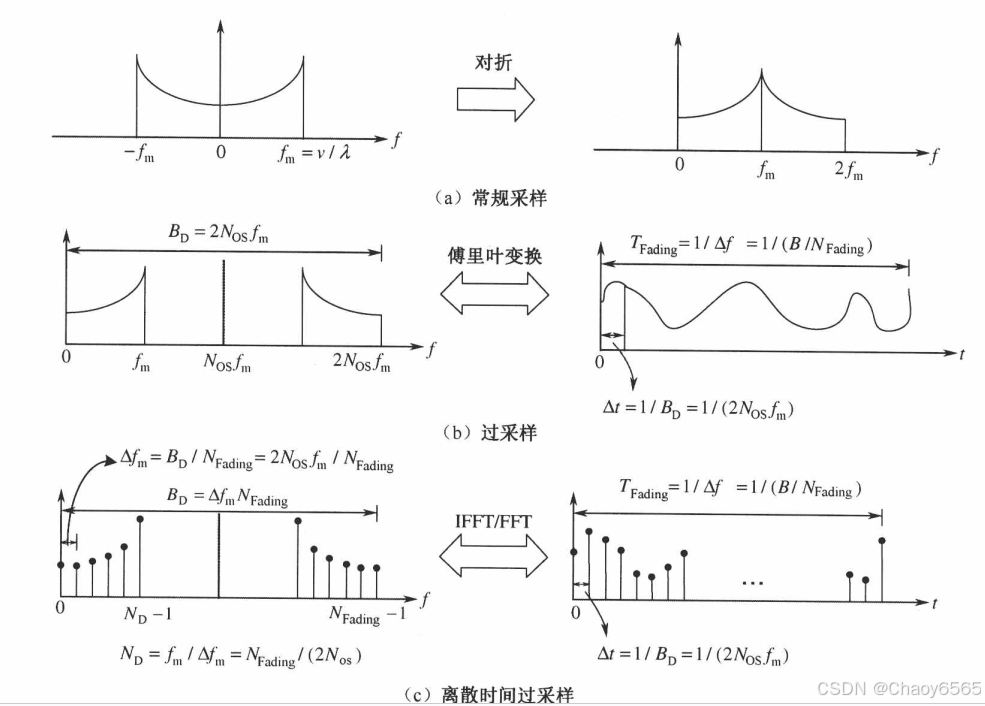
信道响应可通过多普勒谱的离散傅里叶逆变换生成:
h
[
n
]
=
∑
k
=
−
N
Fading
/
2
N
Fading
/
2
−
1
S
[
k
]
e
j
θ
k
e
j
2
π
n
k
/
N
Fading
h[n] = \sum_{k=-N_{\text{Fading}}/2}^{N_{\text{Fading}}/2-1} \sqrt{S[k]} e^{j\theta_k} e^{j2\pi nk/N_{\text{Fading}}} \
h[n]=k=−NFading/2∑NFading/2−1S[k]ejθkej2πnk/NFading
参数说明:
| 符号 | 物理意义 | 计算方式 |
|---|---|---|
| S [ k ] S[k] S[k] | 离散多普勒功率谱 | S [ k ] = S ( f ) ∣ f = k Δ f S[k] = S(f)|_{f=k\Delta f} S[k]=S(f)∣f=kΔf |
| θ k \theta_k θk | 随机相位 | θ k ∼ U [ 0 , 2 π ) \theta_k \sim \mathcal{U}[0,2\pi) θk∼U[0,2π) |
| N Fading N_{\text{Fading}} NFading | 频域采样点数 | N Fading ≥ 2 f d T s N_{\text{Fading}} \geq 2f_dT_s NFading≥2fdTs |
| f d f_d fd | 最大多普勒频移 | f d = v f c / c f_d = vf_c/c fd=vfc/c |
时域 FWGN 模型
在频域 FWGN 模型中,衰落信道的持续时间由IFFT的大小Nad, 和频域过采样系数 Nos共同决定。与之相反,在时域FWGN模型中,衰落信道的持续时间由复高斯随机信号的长度决定。增加经过多普勒滤波器的复高斯随机采样点数,可以简单地扩展仿真区间,所以时域FWGN 模型具有仿真灵活的特性。

除了先前的经典多普勒谱之外,FWGN模型可以使用各种类型的多普勒谱,包括平坦多普勒谱和拉普拉斯多普勒谱。平坦多普勒谱具有恒定的功率谱密度函数(PSD):
S
(
f
)
=
{
1
2
f
m
,
∣
f
∣
≤
f
m
0
,
其他
S(f) = \begin{cases} \frac{1}{2f_m}, & |f| \leq f_m \\ 0, & \text{其他} \end{cases} \
S(f)={2fm1,0,∣f∣≤fm其他
拉普拉斯多普勒功率谱密度(PSD)
S
(
f
)
=
C
1
−
(
f
/
f
m
)
2
⋅
exp
[
−
2
σ
(
∣
θ
−
ϕ
∣
+
e
−
∣
θ
+
ϕ
∣
)
]
S(f) = \frac{C}{\sqrt{1-(f/f_m)^2}} \cdot \exp\left[ -\frac{\sqrt{2}}{\sigma} \left( \left|\theta - \phi\right| + e^{-\left|\theta + \phi\right|} \right) \right] \
S(f)=1−(f/fm)2C⋅exp[−σ2(∣θ−ϕ∣+e−∣θ+ϕ∣)]
| 参数 | 物理含义 | 影响规律 | 典型取值 |
|---|---|---|---|
| σ \sigma σ | 角度扩展标准差 | σ ↑ \sigma \uparrow σ↑ → 谱展宽 | 30°-60° |
| ϕ \phi ϕ | DoM-DoA夹角 | ϕ ≠ 0 \phi \neq 0 ϕ=0 → 谱不对称 | 0°-180° |
| f m f_m fm | 最大多普勒频移 | f m ↑ f_m \uparrow fm↑ → 带宽增大 | v ⋅ f c / c v \cdot f_c/c v⋅fc/c |
Jakes模型
通过对(多个)负正弦波的合成(加权)
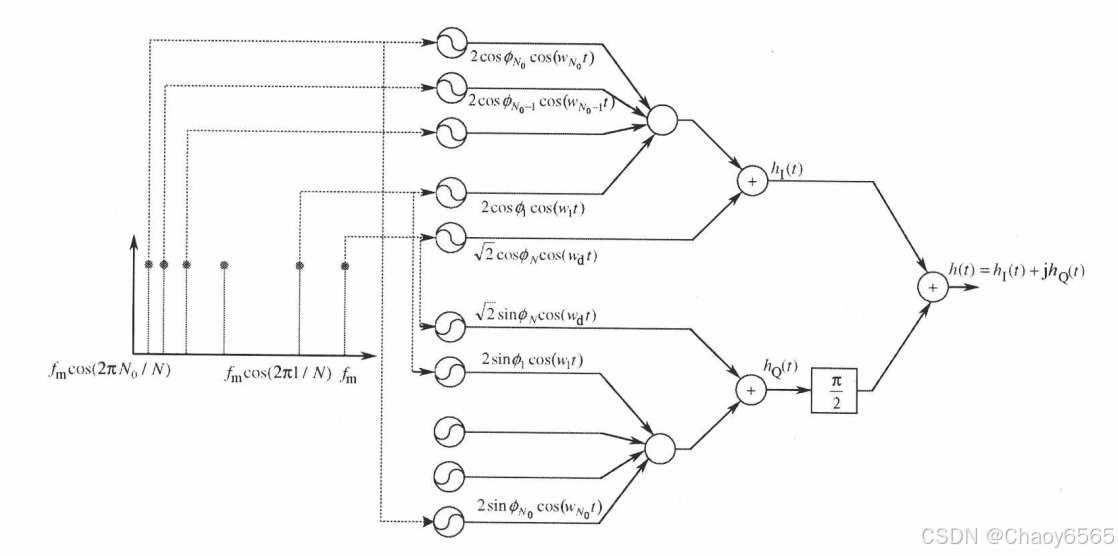
h ( t ) = E 0 2 N 0 + 1 ( h I ( t ) + j h Q ( t ) ) h(t) = \frac{E_0}{\sqrt{2N_0+1}} \left( h_I(t) + jh_Q(t) \right) \ h(t)=2N0+1E0(hI(t)+jhQ(t))
| 符号 | 物理意义 | 单位 | 取值范围/计算方式 |
|---|---|---|---|
| h(t) | 复基带信道冲激响应(时域) | - | 复数(实部+虚部) |
| E 0 E_0 E0 | 衰落信道的平均幅度(归一化参考值) | 无量纲 | 通常设为1(归一化功率) |
| N 0 N_0 N0 | 平面波数量参数 | 无量纲 | N 0 N_0 N0 = (N/2 - 1)/2,N为奇数 |
| h I ( t ) h_I(t) hI(t) | 同相分量(In-phase component) | - | 实数值,多普勒频移的加权和 |
| h Q ( t ) h_Q(t) hQ(t) | 正交分量(Quadrature component) | - | 实数值,多普勒频移的加权和 |
| j | 虚数单位 | - | 满足j² = -1 |
基于射线的信道模型
基于射线的(Ray-based)模型能够考虑空-时相关性,和 Jakes 模型一样,基于射线的模型由到达平面波的总和给出。基于射线的模型能在各种散射环境下模拟移动台周围以任意方向到达的平面波,而且通常不是均匀的功率方位谱(PAS)。与Jakes模型不同,它的多普勒谱不是U形谱,而是依据散射环境的不同而呈不同的形式。

信道脉冲响应公式:
h
u
,
s
,
n
(
t
)
=
P
n
σ
SF
M
∑
m
=
1
M
[
G
BS
(
θ
n
,
m
,
AoD
)
exp
(
j
[
k
d
s
sin
(
θ
n
,
m
,
AoD
)
+
Φ
n
,
m
]
)
×
G
MS
(
θ
n
,
m
,
AoA
)
exp
(
j
k
d
u
sin
θ
n
,
m
,
AoA
)
×
exp
(
j
k
∥
v
∥
cos
(
θ
n
,
m
,
AoA
−
θ
v
)
t
)
]
\begin{aligned} h_{u,s,n}(t) = \sqrt{\frac{P_n\sigma_{\text{SF}}}{M}} \sum_{m=1}^{M} &\left[ \sqrt{G_{\text{BS}}(\theta_{n,m,\text{AoD}})} \exp\left(j[kd_s\sin(\theta_{n,m,\text{AoD}})+\Phi_{n,m}]\right) \right. \\ &\times \left. \sqrt{G_{\text{MS}}(\theta_{n,m,\text{AoA}})} \exp\left(jkd_u\sin\theta_{n,m,\text{AoA}}\right) \right. \\ &\times \left. \exp\left(jk\|v\|\cos(\theta_{n,m,\text{AoA}}-\theta_v)t\right) \right] \end{aligned}
hu,s,n(t)=MPnσSFm=1∑M[GBS(θn,m,AoD)exp(j[kdssin(θn,m,AoD)+Φn,m])×GMS(θn,m,AoA)exp(jkdusinθn,m,AoA)×exp(jk∥v∥cos(θn,m,AoA−θv)t)]
| 符号 | 物理意义 | 单位 | 典型值 |
|---|---|---|---|
| h u , s , n ( t ) h_{u,s,n}(t) hu,s,n(t) | 第s发-第u收天线第n路径响应 | - | 复数 |
| P n P_n Pn | 第n路径功率 | W | 归一化 |
| σ S F σ_SF σSF | 阴影衰落标准差 | dB | 4-10dB |
| M M M | 子径数量 | - | 20(城区) |
| θ n , m , A o D θ_{n,m,AoD} θn,m,AoD | 离开角(AoD) | rad | 3GPP表6.2 |
| θ n , m , A o A θ_{n,m,AoA} θn,m,AoA | 到达角(AoA) | rad | 3GPP表6.2 |
| Φ n , m Φ_{n,m} Φn,m | 随机相位 | rad | U[0,2π) |
| G B S ( θ ) G_BS(θ) GBS(θ) | 基站天线增益 | dBi | 方向图模型 |
| G M S ( θ ) G_MS(θ) GMS(θ) | 终端天线增益 | dBi | 全向天线 |
| k k k | 波数 | rad/m | 2π/λ |
| d s d_s ds | 基站天线间距 | m | 0.5λ |
| d u d_u du | 终端天线间距 | m | 0.5λ |
| ‖ v ‖ ‖v‖ ‖v‖ | 移动速度 | m/s | 0-30m/s |
| θ v θ_v θv | 移动方向 | rad | U[0,2π) |
对于 SISO信道,由于不存在任何的空间相关性,如果去掉所有与空间相关性有关的参数
h
n
(
t
)
=
P
n
M
∑
m
=
1
M
(
exp
(
j
Φ
n
,
m
)
×
exp
(
j
2
π
λ
∥
v
∥
cos
(
θ
n
,
m
,
A
o
A
−
θ
v
)
t
)
)
\begin{align*} h_n(t) &= \sqrt{\frac{P_n}{M}} \sum_{m=1}^{M} \bigg( \exp\Bigl(j\Phi_{n,m}\Bigr) \times \exp\biggl(j\frac{2\pi}{\lambda}\|v\|\cos\Bigl(\theta_{n,m,AoA} - \theta_v\Bigr)t \biggr) \bigg) \\ &\end{align*}
hn(t)=MPnm=1∑M(exp(jΦn,m)×exp(jλ2π∥v∥cos(θn,m,AoA−θv)t))

在基于射线的模型中,对给定 PAS的信道建模时,可以按照PAS给每一子径分配角度和功率在3GPPAd-Hoc组(AHG)的SCM中,考虑了两种不同的方法给每一子径分配功率和角度:均匀功率子径法和离散拉普拉斯法。
频率选择性衰落信道模型
抽头时延线模型


由于一般信道的PDP是基于特定环境(如宏蜂窝或室内)的实际测量值得到的,时延有可能不是采样周期工的整数倍。在这种情况下,为了实现离散的信道仿真器,需要调整PDP。例如,可以利用过采样将抽头时延修正为采样周期的整数倍,然而,这样做会导致FIR 滤波器的抽头数太多。反之,抽头插值、取整或抽头重复采样是实施起来更为简便的方法。接下来,我们介绍取整和抽头插值的方法。我们必须保证抽头调整后信道的特性(如RMS时延扩展)保持不变。
总结
这章看的很痛苦,就不总结了!























 444
444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










