如果想了解更多的知识,可以去我的机器学习之路 The Road To Machine Learning通道
多元函数的泰勒展开Talor以及黑塞矩阵
在学最优化的时候,会遇到很多多元函数的泰勒展开,且很多都是以矩阵形式写的,为了理解更好一点,这里做一些推导
我们先回顾一下,由高等数学知识可知,若一元函数在点的某个邻域内具有任意阶导数
-
一元函数在点 x k x_k xk处的泰勒展开
f ( x ) = f ( x k ) + ( x − x k ) f ′ ( x k ) + 1 2 ! ( x − x k ) 2 f ′ ′ ( x k ) + o n f(x) = f(x_k)+(x-x_k)f'(x_k)+\frac{1}{2!}(x-x_k)^2f''(x_k)+o^n f(x)=f(xk)+(x−xk)f′(xk)+2!1(x−xk)2f′′(xk)+on -
二元函数在 ( x k , y k ) (x_k,y_k) (xk,yk)处的泰勒展开
f ( x , y ) = f ( x k , y k ) + ( x − x k ) f x ′ ( x k , y k ) + ( y − y k ) f y ′ ( x k , y k ) + 1 2 ! ( x − x k ) 2 f x x ′ ′ ( x k , y k ) + 1 2 ! ( x − x k ) ( y − y k ) f x y ′ ′ ( x k , y k ) + 1 2 ! ( x − x k ) ( y − y k ) f y x ′ ′ ( x k , y k ) + 1 2 ! ( y − y k ) 2 f y y ′ ′ ( x k , y k ) + o n f(x,y)=f(x_k,y_k)+(x-x_k)f'_x(x_k,y_k)+(y-y_k)f'_y(x_k,y_k)\\ +\frac1{2!}(x-x_k)^2f''_{xx}(x_k,y_k)+\frac1{2!}(x-x_k)(y-y_k)f''_{xy}(x_k,y_k)\\ +\frac1{2!}(x-x_k)(y-y_k)f''_{yx}(x_k,y_k)+\frac1{2!}(y-y_k)^2f''_{yy}(x_k,y_k)\\ +o^n f(x,y)=f(xk,yk)+(x−xk)fx′(xk,yk)+(y−yk)fy′(xk,yk)+2!1(x−xk)2fxx′′(xk,yk)+2!1(x−xk)(y−yk)fxy′′(xk,yk)+2!1(x−xk)(y−yk)fyx′′(xk,yk)+2!1(y−yk)2fyy′′(xk,yk)+on -
多元函数(n)在点 x k x_k xk处的泰勒展开式为:
f ( x 1 , x 2 , … , x n ) = f ( x k 1 , x k 2 , … , x k n ) + ∑ i = 1 n ( x i − x k i ) f x i ′ ( x k 1 , x k 2 , … , x k n ) + 1 2 ! ∑ i , j = 1 n ( x i − x k i ) ( x j − x k j ) f i j ′ ′ ( x k 1 , x k 2 , … , x k n ) + o n f(x^1,x^2,\ldots,x^n)=f(x^1_k,x^2_k,\ldots,x^n_k)+\sum_{i=1}^n(x^i-x_k^i)f'_{x^i}(x^1_k,x^2_k,\ldots,x^n_k)\\ +\frac1{2!}\sum_{i,j=1}^n(x^i-x_k^i)(x^j-x_k^j)f''_{ij}(x^1_k,x^2_k,\ldots,x^n_k)\\ +o^n f(x1,x2,…,xn)=f(xk1,xk2,…,xkn)+i=1∑n(xi−xki)fxi′(xk1,xk2,…,xkn)+2!1i,j=1∑n(xi−xki)(xj−xkj)fij′′(xk1,xk2,…,xkn)+on -
把Taylor展开式写成矩阵的形式:
f ( x ) = f ( x k ) + [ ∇ f ( x k ) ] T ( x − x k ) + 1 2 ! [ x − x k ] T H ( x k ) [ x − x k ] + o n f(\mathbf x) = f(\mathbf x_k)+[\nabla f(\mathbf x_k)]^T(\mathbf x-\mathbf x_k)+\frac1{2!}[\mathbf x-\mathbf x_k]^TH(\mathbf x_k)[\mathbf x-\mathbf x_k]+o^n f(x)=f(xk)+[∇f(xk)]T(x−xk)+2!1[x−xk]TH(xk)[x−xk]+on
其中:
H ( x k ) = [ ∂ 2 f ( x k ) ∂ x 1 2 ∂ 2 f ( x k ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x k ) ∂ x 1 ∂ x n ∂ 2 f ( x k ) ∂ x 2 ∂ x 1 ∂ 2 f ( x k ) ∂ x 2 2 ⋯ ∂ 2 f ( x k ) ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ( x k ) ∂ x n ∂ x 1 ∂ 2 f ( x k ) ∂ x n ∂ x 2 ⋯ ∂ 2 f ( x k ) ∂ x n 2 ] H(\mathbf x_k)= \left[ \begin{matrix} \frac{\partial^2f(x_k)}{\partial x_1^2} & \frac{\partial^2f(x_k)}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2f(x_k)}{\partial x_1\partial x_n} \\ \frac{\partial^2f(x_k)}{\partial x_2 \partial x_1} & \frac{\partial^2f(x_k)}{\partial x_2^2} & \cdots & \frac{\partial^2f(x_k)}{\partial x_2\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2f(x_k)}{\partial x_n\partial x_1} & \frac{\partial^2f(x_k)}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2f(x_k)}{\partial x_n^2} \\ \end{matrix} \right] H(xk)=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f(xk)∂x2∂x1∂2f(xk)⋮∂xn∂x1∂2f(xk)∂x1∂x2∂2f(xk)∂x22∂2f(xk)⋮∂xn∂x2∂2f(xk)⋯⋯⋱⋯∂x1∂xn∂2f(xk)∂x2∂xn∂2f(xk)⋮∂xn2∂2f(xk)⎦⎥⎥⎥⎥⎥⎤ -
当为二元时
∇ f ( x k ) = [ f x ′ ( x k , y k ) f y ′ ( x k , y k ) ] \nabla f(x_k) = \left[ \begin{matrix} & f_x' ( x_k , y_k) &\\ & f'_y( x_k , y_k) &\\ \end{matrix} \right] ∇f(xk)=[fx′(xk,yk)fy′(xk,yk)]
x
−
x
k
=
[
x
−
x
k
y
−
y
k
]
x - x_k = \begin{bmatrix} & x - x_k &\\ & y - y_k \end{bmatrix}
x−xk=[x−xky−yk]
H
(
x
k
)
=
[
f
x
x
′
′
(
x
k
,
y
k
)
f
x
y
′
′
(
x
k
,
y
k
)
f
y
x
′
′
(
x
k
,
y
k
)
f
y
y
′
′
(
x
k
,
y
k
)
]
H(x_k) = \begin{bmatrix} & f_{xx}''(x_k,y_k) & f''_{xy}(x_k,y_k) &\\ & f''_{yx}(x_k,y_k) & f''_{yy}(x_k,y_k) &\\ \end{bmatrix}
H(xk)=[fxx′′(xk,yk)fyx′′(xk,yk)fxy′′(xk,yk)fyy′′(xk,yk)]
具体推导
可能这样还是有点抽象,那我们来一个具体一点的,帮助我们理解
由前面可知二元函数
f
(
x
1
,
x
2
)
f(x_1,x_2)
f(x1,x2)在
X
(
0
)
(
x
1
(
0
)
,
x
2
(
0
)
)
X^{(0)}(x_1^{(0)},x_2^{(0)})
X(0)(x1(0),x2(0))点的泰勒展开式为:
f
(
x
1
,
x
2
)
=
f
(
x
1
(
0
)
,
x
2
(
0
)
)
+
∂
f
∂
x
1
∣
X
(
0
)
Δ
x
1
+
∂
f
∂
x
2
∣
X
(
0
)
Δ
x
2
+
1
2
!
∂
2
f
∂
x
1
2
∣
X
(
0
)
Δ
x
1
2
+
1
2
!
∂
2
f
∂
x
1
∂
x
2
∣
X
(
0
)
Δ
x
1
Δ
x
2
+
1
2
!
∂
2
f
∂
x
2
∂
x
1
∣
X
(
0
)
Δ
x
1
Δ
x
2
+
1
2
!
∂
2
f
∂
x
2
2
∣
X
(
0
)
Δ
x
2
2
+
.
.
.
f(x_1,x_2) = f(x_1^{(0)},x_2^{(0)}) + \frac{\partial f}{\partial x_1}\bigg|_{X^{(0)}} \Delta x_1+ \frac{\partial f}{\partial x_2}\bigg|_{X^{(0)}} \Delta x_2\\ {+} \frac{1}{2!} \frac{\partial^2 f}{\partial x_1^2}\bigg|_{X^{(0)}} \Delta x_1^2+ \frac{1}{2!}\frac{\partial^2 f}{\partial x_1 \partial x_2}\bigg|_{X^{(0)}} \Delta x_1 \Delta x_2 + \\ \frac{1}{2!}\frac{\partial^2 f}{\partial x_2 \partial x_1}\bigg|_{X^{(0)}} \Delta x_1 \Delta x_2 + \frac{1}{2!}\frac{\partial^2 f}{\partial x_2^2}\bigg|_{X^{(0)}} \Delta x_2^2 + ...
f(x1,x2)=f(x1(0),x2(0))+∂x1∂f∣∣∣∣X(0)Δx1+∂x2∂f∣∣∣∣X(0)Δx2+2!1∂x12∂2f∣∣∣∣X(0)Δx12+2!1∂x1∂x2∂2f∣∣∣∣X(0)Δx1Δx2+2!1∂x2∂x1∂2f∣∣∣∣X(0)Δx1Δx2+2!1∂x22∂2f∣∣∣∣X(0)Δx22+...
其中,
Δ
x
1
=
x
1
−
x
1
(
0
)
,
Δ
x
2
=
x
2
−
x
2
(
0
)
\Delta x_1 = x_1 - x_1^{(0)},\Delta x_2 = x_2 - x_2^{(0)}
Δx1=x1−x1(0),Δx2=x2−x2(0)
若写成矩阵形式,就是如下
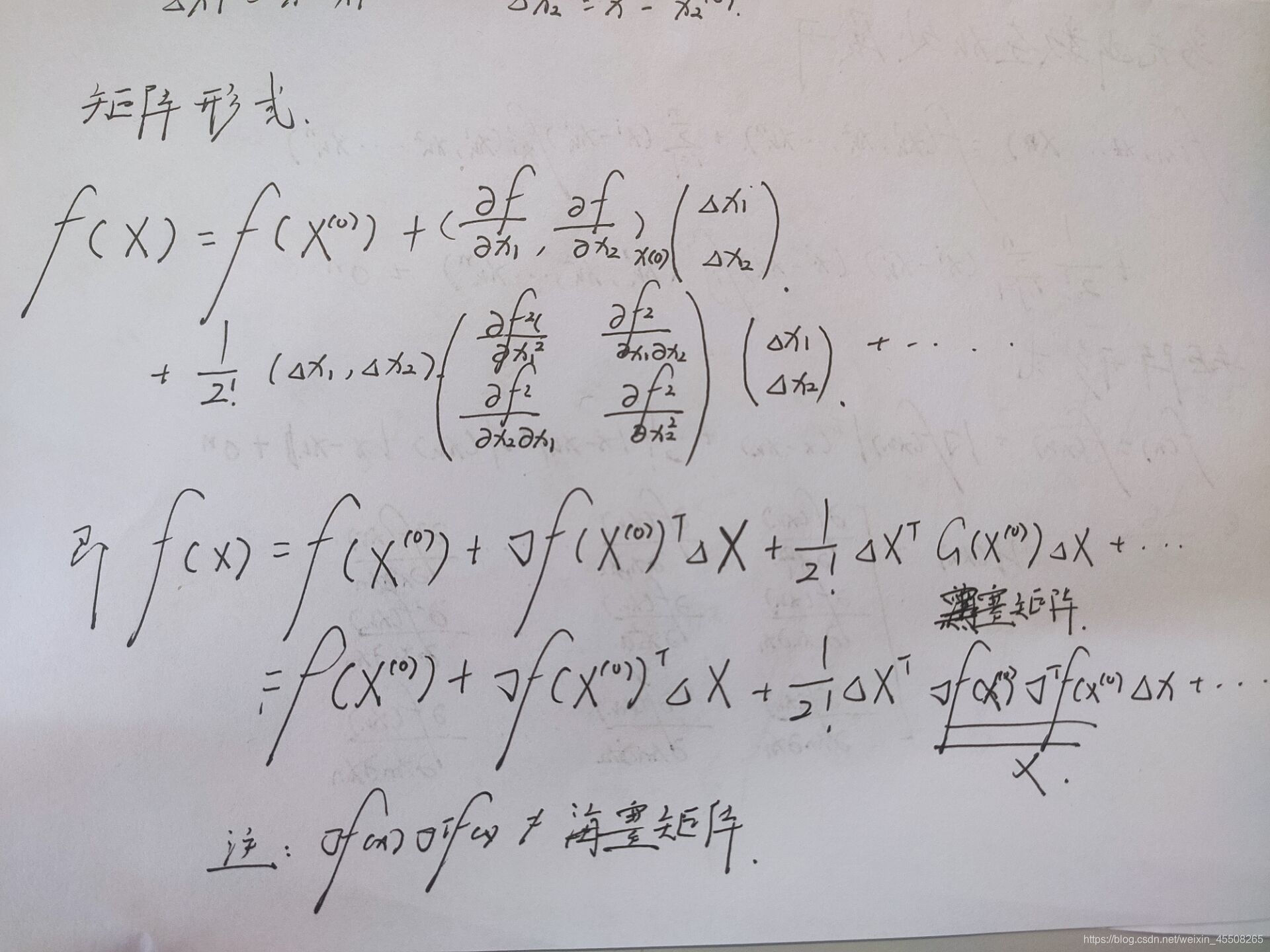
所以,写成矩阵形式
f
(
x
)
=
f
(
x
k
)
+
[
∇
f
(
x
k
)
]
T
(
Δ
x
)
+
1
2
!
[
(
Δ
x
)
]
T
H
(
x
k
)
[
(
Δ
x
)
]
+
o
n
f(\mathbf x) = f(\mathbf x_k)+[\nabla f(\mathbf x_k)]^T(\mathbf \Delta x)+\frac1{2!}[(\mathbf \Delta x)]^TH(\mathbf x_k)[(\mathbf \Delta x)]+o^n
f(x)=f(xk)+[∇f(xk)]T(Δx)+2!1[(Δx)]TH(xk)[(Δx)]+on
注:
∇
f
(
x
(
0
)
)
∇
f
T
(
x
(
0
)
)
\nabla f(x_{(0)}) \nabla f^T(x_{(0)})
∇f(x(0))∇fT(x(0))不为在
x
(
0
)
x^{(0)}
x(0)的黑塞矩阵(可证明)
对称性
除此之外,我们二阶偏导数还有一个性质
如果函数
f
f
f在
D
D
D区域内二阶连续可导,那么
f
f
f黑塞矩阵
H
(
f
)
在
D
H(f)在D
H(f)在D区域内为对称矩阵。
原因:如果函数
f
f
f的二阶偏导数连续,则二阶偏导数的求导顺序没有区别,即
∂
∂
x
(
∂
f
∂
y
)
=
∂
∂
y
(
∂
f
∂
x
)
\frac{\partial}{\partial x}(\frac{\partial f}{\partial y}) = \frac{\partial}{\partial y}(\frac{\partial f}{\partial x})
∂x∂(∂y∂f)=∂y∂(∂x∂f)
则对于矩阵
H
(
f
)
H(f)
H(f),由
H
i
,
j
(
f
)
=
H
j
,
i
(
f
)
H_{i,j}(f) = H_{j,i}(f)
Hi,j(f)=Hj,i(f),所以
H
(
f
)
H(f)
H(f)为对称矩阵
利用黑塞矩阵判定多元函数的极值
定理
设n多元实函数
f
(
x
1
,
x
2
,
…
,
x
n
)
f(x_1,x_2,\ldots,x_n)
f(x1,x2,…,xn)在点
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_0(a_1,a_2,\ldots,a_n)
M0(a1,a2,…,an)的邻域内有二阶连续偏导,若有:
∂
f
∂
x
j
∣
(
a
1
,
a
2
,
…
,
a
n
)
=
0
,
j
=
1
,
2
,
…
,
n
\frac{\partial f}{\partial x_j} \bigg|_{(a_1,a_2,\ldots,a_n)} = 0,j=1,2,\ldots,n
∂xj∂f∣∣∣∣(a1,a2,…,an)=0,j=1,2,…,n
并且
H
=
[
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
⋮
⋱
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
]
H= \left[ \begin{matrix} \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2f}{\partial x_1\partial x_n} \\ \frac{\partial^2f}{\partial x_2 \partial x_1} & \frac{\partial^2f}{\partial x_2^2} & \cdots & \frac{\partial^2f}{\partial x_2\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2f}{\partial x_n\partial x_1} & \frac{\partial^2f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2f}{\partial x_n^2} \\ \end{matrix} \right]
H=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤
则有如下结果
(1)当A正定矩阵时,
f
(
x
1
,
x
2
,
…
,
x
n
)
f(x_1,x_2,\ldots,x_n)
f(x1,x2,…,xn)在
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_0(a_1,a_2,\ldots,a_n)
M0(a1,a2,…,an)处是极小值;
(2)当A负定矩阵时,
f
(
x
1
,
x
2
,
…
,
x
n
)
f(x_1,x_2,\ldots,x_n)
f(x1,x2,…,xn)在
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_0(a_1,a_2,\ldots,a_n)
M0(a1,a2,…,an)处是极大值;
(3)当A不定矩阵时,
M
0
(
a
1
,
a
2
,
…
,
a
n
)
M_0(a_1,a_2,\ldots,a_n)
M0(a1,a2,…,an)不是极值点。
(4)当A为半正定矩阵或半负定矩阵时, 是“可疑”极值点,尚需要利用其他方法来判定。
























 5658
5658











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










