Acwing1027. 方格取数

题意:

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

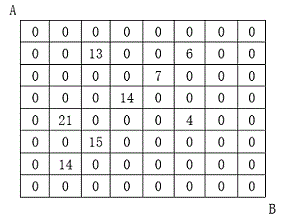
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 1 开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N < = 10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

分析:

既然走了两次而且两次的总步数是一样的,那么可以两个一起走,然后对于当前时刻,两条路有3种走法,下下,下右,右右,然后如果这一步他们到达的位置不同,就加上两个位置上的数,如果走到一个格子了,就只需要算一次就好了.
那么我们用dp[k][i1][i2]表示第k步一个走到(i1, k - i1),一个走到(i2 , k - i2)的最大值,那么分别能够从三个方向转移过来,取三次MAX就可以了.

int dp[2 * MAXN][MAXN][MAXN];
int mp[MAXN][MAXN];
//dp[k][i1][i2]表示走到(i1,k-i1),(i2,k-i2)的MAX 
int n;

int main(){
	scanf("%d",&n);
	memset(mp,0,sizeof(mp));
	int a,b,c;
	
	while(~scanf("%d%d%d",&a,&b,&c) && (a || b || c)){
		mp[a][b] = c;
	}
	for(int k=2;k<=2*n;k++){
		for(int i1 = 1;i1 <= n;i1 ++){
			for(int i2 = 1;i2 <= n;i2 ++){
				int j1 = k - i1,j2 = k - i2;
				if(j1 <= n && j2 <= n && j1 >= 1 && j2 >= 1){
					int w = mp[i1][j1];
				    if(i1 != i2)w += mp[i2][j2];
					dp[k][i1][i2] = max(dp[k][i1][i2],dp[k-1][i1-1][i2-1] + w);  //下下
			 		dp[k][i1][i2] = max(dp[k][i1][i2],dp[k-1][i1-1][i2] + w);  //下右 
			 		dp[k][i1][i2] = max(dp[k][i1][i2],dp[k-1][i1][i2-1] + w);  //右下
			 		dp[k][i1][i2] = max(dp[k][i1][i2],dp[k-1][i1][i2] + w);  //右右 
				}
			}
		}
	}
	printf("%d\n",dp[2*n][n][n]); 
	return 0;
}