背包问题看这个就够啦：01背包、完全背包、多重背包、分组背包~

注: 并不仔细介绍每个问题的含义等(已有很多大佬仔细写过)，这里列出学习笔记，和各类问题比较优美代码。代码形式统一，便于观看。

背包问题

1. 01背包

每件物品只能用一次

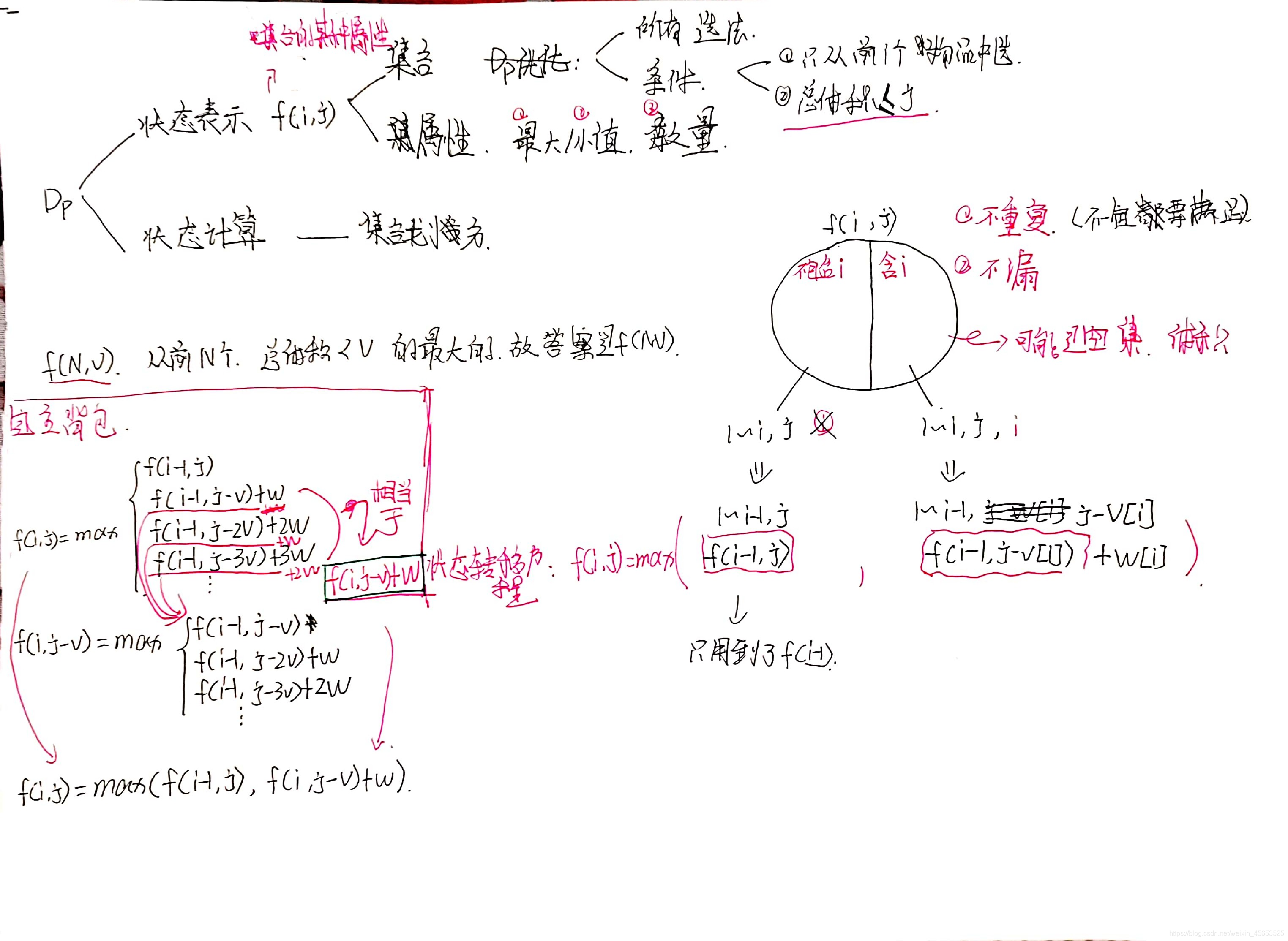
f(N,V) 从前N个物品中选，总体积<=V中的最大价值的方案，所以最后的答案是f(N,V)；

f(i, j) = max( f(i -1, j), f(i-1, j-V[i]) + W[i]);

二维朴素算法：

#include <iostream>
#include <algorithm>
using namespace std;

const int MAX_N = 1010;
int W[MAX_N], V[MAX_N];
int f[MAX_N][MAX_N];
int N, M;

int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
        cin >> V[i] >> W[i];
    for (int i = 1; i <= N; i++)
    {
        for (int j = 0; j <= M; j++)
        {
            // 不选i 一定可以成立
            f[i][j] = f[i - 1][j];
            // 选i 不一定，判断容量
            if (j >= V[i])
                f[i][j] = max(f[i - 1][j], f[i - 1][j - V[i]] + W[i]);
        }
    }
    cout << f[N][M];
    return 0;
}

一维优化算法：

#include <iostream>
#include <algorithm>
using namespace std;

const int MAX_N = 1010;
int W[MAX_N], V[MAX_N];
int f[MAX_N]; // 一层
int N, M;

int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
        cin >> V[i] >> W[i];
    for (int i = 1; i <= N; i++)
    {
        // 从大到小
        for (int j = M; j >= V[i]; j--)
        {
            // 原因是：
            // 现在f[j]其实是用的上一层的
            // 即f[i-1][j]
            f[j] = max(f[j], f[j - V[i]] + W[i]);
        }
    }
    cout << f[M];
    return 0;
}

2. 完全背包

每件物品有无限个

朴素算法——枚举个数k

k为1的时候最多V次，那么
$$O(N\ast V\ast V);$$

#include <iostream>
#include <algorithm>
using namespace std;

const int MAX_N = 1010;
int w[MAX_N], v[MAX_N];
int f[MAX_N][MAX_N];
int N, M;

int main()
{
    cin >> N >> M;

    for (int i = 1; i <= N; i++)
        // cin >> v[i] >> w[i];
        scanf("%d%d", &v[i], w[i]);

    for (int i = 1; i <= N; i++)
    {
        for (int j = 0; j <= M; j++)
        {
            for (int k = 0; k * v[i] <= j; k++)
            {
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }
    cout << f[N][M] << endl;
    return 0;
}

二维算法：
$$f(i,j)=max(f(i-1,j),f(i-1,j-v)+w...f(i-1,j-kv)+kw)$$
而
$$f(i,j-v)=max(f(i-1,j-v),f(i-1,j-2v)+w...f(i-1,j-kv)+(k-1)w)$$
得到：
$$f(i,j)=max(f(i-1,j),f(i,j-v)+w)$$

#include <iostream>
#include <algorithm>
using namespace std;

const int MAX_N = 1010;
int W[MAX_N], V[MAX_N];
int f[MAX_N][MAX_N];
int N, M;

int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
        cin >> V[i] >> W[i];
    for (int i = 1; i <= N; i++)
    {
        for (int j = 0; j <= M; j++)
        {
            // 第一种状态 选0个
            f[i][j] = f[i - 1][j];
            // 第二种状态 选k个
            if (j >= V[i])
                f[i][j] = max(f[i][j], f[i][j - V[i]] + W[i]);
        }
    }
    cout << f[N][M];
    return 0;
}

一维优化算法：

有了01背包的经验，完全背包优化成1维就感觉很容易了

#include <iostream>
#include <algorithm>
using namespace std;

const int MAX_N = 1010;
int W[MAX_N], V[MAX_N];
int f[MAX_N];
int N, M;

int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
        cin >> V[i] >> W[i];
    for (int i = 1; i <= N; i++)
    {
        // 因为二维的是再当前层(i) 所以是从小到大
        // 和01背包代码的不同就是方向相反
        for (int j = V[i]; j <= M; j++)
        {
            f[j] = max(f[j], f[j - V[i]] + W[i]);
        }
    }
    cout << f[M];
    return 0;
}

3. 多重背包

每件物品有有限个 s[i]

朴素算法——枚举个数k

和完全背包的朴素算法一样，就是多个数限制

#include <iostream>
#include <algorithm>
using namespace std;

int N, M;
const int MAX_N = 110;
int W[MAX_N], V[MAX_N], S[MAX_N];
int f[MAX_N][MAX_N];

int main()
{
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
        cin >> V[i] >> W[i] >> K[i];

    for (int i = 1; i <= N; i++)
        for (int j = 0; j <= M; j++)
            for (int k = 0; k <= S[i] && k * V[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * V[i]] + W[i] * k);

    cout << f[N][M];
    return 0;
}

二进制优化：

把原来Si个打包变成新的logSi个，然后进行01背包

#include <iostream>
using namespace std;

const int MAX_N = 15000, MAX_M = 2010; // N*logS 新的N的范围
int f[MAX_M];
int V[MAX_N], W[MAX_N];

int N, M;
int main()
{
    cin >> N >> M;
    // 新的N
    int cnt = 0;
    for (int i = 1; i <= N; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;

        // k是s个打包的编号
        int k = 1;
        // k = 1,2,4,8,32,,,C
        while (k <= s)
        {
            cnt++;
            V[cnt] = v * k;
            W[cnt] = w * k;
            s -= k;
            k *= 2;
        }
        if (s > 0)
        {
            cnt++;
            V[cnt] = s * v;
            W[cnt] = s * w;
        }
    }
    // 来一遍01背包
    N = cnt;
    for (int i = 1; i <= N; i++)
        for (int j = M; j >= V[i]; j--)
            f[j] = max(f[j], f[j - V[i]] + W[i]);

    cout << f[M];
    return 0;
}

4. 分组背包

有N组，每组有若干个，每组最多只能选一个物品

#include <iostream>
using namespace std;

const int MAX_N = 110;
int f[MAX_N];
int W[MAX_N][MAX_N], V[MAX_N][MAX_N]；// 第i组的第k个的~
int S[MAX_N];

int main()
{
    int N, M;
    cin >> N >> M;

    for (int i = 1; i <= N; i++)
    {
        cin >> S[i]; // 一组中物品的个数
        for (int k = 0; k < S[i]; k++)
            cin >> V[i][k] >> W[i][k];
    }

    for (int i = 1; i <= N; i++)
        for (int j = M; j >= 0; j--)
            for (int k = 0; k < S[i]; k++)
                if(j >= V[i][k])
                    f[j] = max(f[j], f[j - V[i][k]] + W[i][k]);

    cout << f[M];

    return 0;
}