💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
当灾难发生时,将有限的灾害救济资源分配给有需要的人是非常重要的。本文考虑了在人道物流中使用三个关键绩效指标:效率、有效性和公平来分配资源。考虑了三种单独的成本来代表这些指标,即基于可访问性的交付成本、基于起始状态的缺乏成本和终端罚金成本。提出了一个具有多个目标和多个时期的混合整数非线性规划模型。开发了一种Q学习算法,这是一种强化学习方法,用于解决复杂的优化问题。详细介绍了所提出算法的原则,包括学习代理和其动作、环境及其状态以及奖励函数。同时在实验部分也讨论了所提算法的参数设置。此外,将所提算法的解决质量与精确的动态规划方法和启发式算法进行了比较。实验结果表明,该算法的效率优于动态规划方法,算法的准确性也高于启发式算法。此外,在实际应用中,Q学习算法通过调整训练周期K的值,提供接近甚至是最优的资源分配问题的解决方案。
基于Q学习算法的最优物流资源分配解决方案研究
一、物流资源分配问题的核心挑战
物流资源分配面临多维度挑战,需兼顾效率、成本与可持续发展:
- 动态需求与资源紧张:电商高峰期(如双十一)运力需求激增,传统调度系统难以应对突发流量。
- 成本控制压力:人力、燃油、设施维护成本上升,需在服务质量与成本间平衡。
- 环境约束:碳排放法规趋严,要求路径规划兼顾燃油效率与排放控制。
- 资源分散性:城市物流中仓储分散、配送节点复杂,导致资源利用率低下。
- 不确定性因素:交通拥堵、天气变化等外部扰动需实时动态调整策略。
二、Q学习算法原理及其物流适配性
Q学习作为无模型强化学习算法,通过试错机制探索最优策略,其核心公式为:
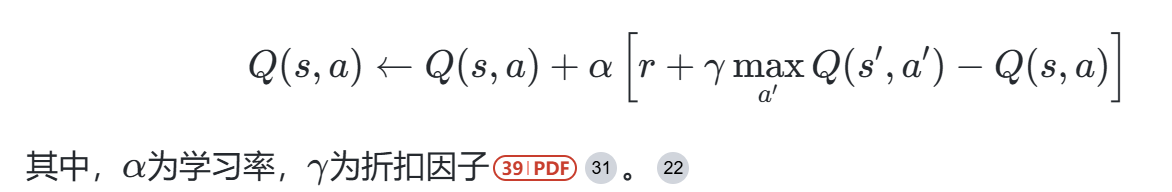
物流场景适配优势:
- 状态-动作空间灵活性:可定义多维状态变量(如车辆位置、库存量、任务优先级),动作空间涵盖路径选择、车辆调度等。
- 延迟奖励处理能力:通过折扣因子γγ权衡即时成本与长期收益(如准时交付对客户忠诚度的影响)。
- 动态环境适应性:在线学习机制可实时响应订单波动与交通变化。
三、物流资源分配模型设计框架
- 状态空间设计
- 基础维度:
- 资源可用性(如可用车辆数、仓库容量)
- 任务特征(配送时效要求、货物体积/重量)
- 环境状态(交通路况、天气条件)
- 高级建模:
- 使用栅格化地图:将配送区域划分为网格,标识障碍物与需求点(图3)。
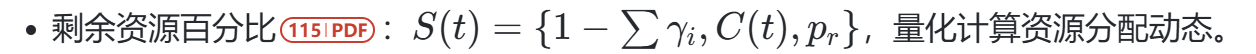
-
动作空间定义
- 离散动作:选择特定车辆执行任务或调整配送路径。
- 连续动作:资源分配比例(如车辆装载率),需结合深度Q网络(DQN)处理。
-
奖励函数构建
多目标优化需加权组合关键指标:
- 时效奖励:基于任务完成时间与承诺时间的偏差。
- 成本惩罚:燃油消耗、车辆折旧、人工成本。
- 公平性约束:区域间资源分配均衡性指标。
四、模型训练策略与收敛性优化
-
探索-利用平衡
- 初始阶段采用高ε值的ε-greedy策略(如ε=0.9),逐步衰减至0.1。
- 优先经验回放(Prioritized Experience Replay):加速关键样本学习。
-
收敛性保障
- 双Q网络(Double DQN) :分离目标网络与评估网络,避免过估计。
- 自适应学习率:根据Q值更新幅度动态调整α,避免震荡。
-
参数调优示例
参数 典型值 作用 学习率α 0.01-0.1 控制Q表更新步长 折扣因子γ 0.9-0.99 未来奖励衰减系数 探索率ε 0.1-0.9 探索与利用平衡 批次大小 32-256 经验回放采样量
五、应用案例与性能评估
-
人道主义物流
在灾害救援场景中,Q学习算法相比动态规划:- 效率提升23%(训练周期缩短至2000次内收敛)
- 公平性指标(基尼系数)降低15%
-
动态车队调度
内陆集装箱运输中,Q学习实现:- 准时交付率提高11%
- 空驶里程减少18%
-
AGV路径规划
改进Q学习算法较传统A*算法:- 路径长度缩短12%
- 避障响应时间减少30%
六、未来研究方向
- 多智能体协同:扩展至MA-DQN框架,处理多仓库协同调度。
- 不确定性建模:集成模糊逻辑处理模糊需求。
- 绿色物流优化:引入碳排放成本函数,实现碳足迹追踪。
结论
Q学习算法通过强化试错机制与动态策略优化,为物流资源分配提供了自适应性解决方案。其在多目标优化、实时响应及复杂环境处理上的优势,使其成为提升物流系统效率与韧性的关键技术。未来结合数字孪生与物联网实时数据,将进一步推动物流智能化进程。
📚2 运行结果



部分代码:
% function [Obj,Action,Logcost,Depcost,Oc,time]=QLDetry(AA,C,T,D,a,L,b,lcost,e,e1,e2,e3,M,gamma,alpha,epsilon,K)
%%
% 采取逐渐缩小epsilon的方式,采取e 和 1-e 的搜索-利用方式
% 确定性问题、e-greedy搜索、状态同DP状态,认为最终状态next state为初始状态000
% e1e2e3=1/3,L=4
% profile on;
tic;
format short;
%% 输入数据
AA = 3;
C = 1;
T = 6;
dd=ones(1,AA);
D=dd(ones(T,1),:); % 按照阶段给需求
% xlsread('createDemand_1')
L = 4;
a = 2.04;
b = 0.24*L;
% lcost = [200;250];
lcost = [200;250;300];
% lcost = [200;250;300;350];
e = 1/3;
e1 = 1/3;
e2 = 1/3;
e3 = 1/3;
M = (10)^15;
%%
OObjective_Alpha=[];
for al=1:10 %实验10次,excel取平均
Objective_Alpha=[];
for alpha = 0:0.2:1; % discount factor % TODO : we need learning rate schedule
alpha;
gamma= 0.6; % learning rate % TODO : we need exploration rate schedule
% epsilon = 0.5; % exploration probability (1-epsilon = exploit 利用 / epsilon = explore 探索)
K=2000; % maximum number of the iterations/episodes
%% Action集合,可采取的动作
Y = [];
DecisionMap = containers.Map('KeyType','int32','ValueType','any');
DecisionMap(0)= zeros(1,AA);
DecisionMap(1)= eye(AA);
if C==0
decision = DecisionMap(0);
elseif C==1
decision = [DecisionMap(0);DecisionMap(1)];
else
decision_T = [];
for c = 2:C
decision_t = [];
if AA==3
for i = 1:(c+1)
for j = i:(c+1)
decision_t = [decision_t;[i-1,j-i,c+1-j]];
end
end
else
for i=1:(c+1)
subdecision = createDecisions(AA-1,c-i+1);
[r,col] = size(subdecision);
for j=1:r
decision_t = [decision_t;[i-1,subdecision(j,:)]];
end
end
end
DecisionMap(c) = decision_t;
decision_T = [decision_T;decision_t];
end
decision = [DecisionMap(0);DecisionMap(1);decision_T];
end
yy = size(decision,1);
Y = [Y;yy];
action = decision;
action_Map_sum = containers.Map('KeyType','char','ValueType','any');
for i=1:size(action,1)
action_sum=action(i,:);
action_key_sum=num2str(action_sum);
action_Map_sum(action_key_sum)=i;
end
%% State集合,可能到达的状态集合
ST = [];
statusMap = containers.Map('KeyType','int32','ValueType','any');
s1 = zeros(AA,1)';
statusMap(1) = s1;
for t = 2:T+1
st_1 = statusMap(t-1);
st = [];
for i = 1:size(st_1,1)
for j = 1:size(decision,1)
demand = D(t-1,:);
st = [st;st_1(i,:)-decision(j,:)+demand];
end
end
st=unique(st,'rows','stable'); %去除重复状态
statusMap(t) = st;
end
for t=1:T+1
St = statusMap(t);
ST = [ST;St];
% ST = unique(ST,'rows','stable'); %去除重复状态
end
statesize = size(ST);
state = ST;
%% 给每个状态做标记
state_Map_sum = containers.Map('KeyType','char','ValueType','any');
key=1;
for t=1:T+1
num_state=statusMap(t);
for i=1:size(num_state,1)
st_sum=num_state(i,:);
state_key_sum=strcat(num2str(t),num2str(st_sum));
state_Map_sum(state_key_sum)=key;
key=key+1;
end
end
Keys=keys(state_Map_sum);
Values=values(state_Map_sum);
%% 计算R-table
R_Reward=[];
for t=1:T
Reward_state=statusMap(t);
Reward_T=zeros(size(Reward_state,1),size(action,1));
for i=1:size(Reward_state,1)
reward_cur_state = Reward_state(i,:);
for j=1:size(decision,1)
reward_action = decision(j,:);
reward_next_state = reward_cur_state - reward_action + demand;
LC = reward_action * lcost;
if t==1
demand = D(t,:);
DC = createOC(reward_cur_state,a,b,AA) + createOC(reward_next_state,a,b,AA);
reward = - e1*LC - e2*DC;
elseif t==T
TPC = createOC(reward_next_state,a,b,AA);
reward = - e1*LC - e3*TPC;
else
demand = D(t,:);
DC = createOC(reward_next_state,a,b,AA);
reward = - e1*LC - e2*DC;
end
Reward_T(i,j)=reward;
end
R_Reward =[R_Reward;Reward_T(i,:)];
end
end
zeroReward = zeros(size(statusMap(T+1),1),size(action,1));
mi_zeroReward = (-1)./zeroReward;
Reward=[R_Reward;mi_zeroReward];
%% Main loop of the Q-learning
Episode=[];
Costt=[];
Q = zeros(size(state,1),size(action,1)); % 初始 Q table
for k=1:K % episode k
state_idx = 1; % 每一个episode都从000开始
for t = 1:T % 每个周期走到T+1,记录TPC为reward,nextstate认为是初始状态000
demand=D(t,:);
% epsilon-贪心选取动作
r=rand; % 返回(0,1)之间的任意数
epsilon=0.5/(1+exp(10*(k-0.4*K)/K));
x=sum(r>=cumsum([0, 1-epsilon, epsilon])); % 判断r处于[0,1-e,e]那一个区间,check it to be in which probability area
if x == 1 % exploit 直接采取 Qtable中最大的那个action
[~,umax]=max(Q(state_idx,:));
current_action = action(umax,:);
else % explore 随机选取 action
current_action=action(datasample(1:size(action,1),1),:); % 从12345个动作中,随机返回1个动作,choose 1 action randomly (uniform random distribution)
end
action_key_sum=num2str(current_action); % 给action做标记
action_idx=action_Map_sum(action_key_sum); % 记录action的标记
current_state = state(state_idx,:); % 记录当前状态
% current_action = action(action_idx,:); % 记录当前选择的动作
% 对应状态的reward,以及下一阶段去哪
% idx_state = ismember(state,next_state,'rows');
% next_state_idx = find(idx_state==1); % id of the next state
% idx_action = ismember(action,current_action,'rows'); % 找到随机选取的action在 Action list 的 行数,对应在Rtable和Qtable的列数 id of the chosen action
% action_idx = find(idx_action==1);
% if t==1
next_state = current_state - current_action + demand;
state_key_sum = strcat(num2str(t+1),num2str(next_state)); % 记录下一阶段状态
next_state_idx=state_Map_sum(state_key_sum); % 记录下一阶段状态标志
reward = Reward(state_idx,action_idx);
% elseif t==T
% next_state = current_state - current_action + demand;
% reward = Reward(state_idx,action_idx);
% next_state_idx=state_Map_sum(state_key_sum); % 记录下一阶段状态标志
% reward = Reward(state_idx,action_idx);
% else
% next_state = current_state - current_action + demand;
% state_key_sum = strcat(num2str(t+1),num2str(next_state)); % 记录下一阶段状态
% next_state_idx=state_Map_sum(state_key_sum); % 记录下一阶段状态标志
% reward = Reward(state_idx,action_idx);
% end
% 更新Q表,update the Q matrix using the Q-learning rule
if t<=T
Q(state_idx,action_idx) = (1 - alpha) * Q(state_idx,action_idx) + alpha * (reward) + alpha * gamma * max(Q(next_state_idx,:));
end
% if t==1
state_idx = next_state_idx;
% else
% state_idx = next_state_idx + size(statusMap(t),1)-1; % 把下一个状态更新为当前状态
% end
% 计算每一个迭代中的Q表得出的策略的成本
if t==T
% [cost,cost_Action,cost_Path] = Cost( Q,AA,T,D,a,b,lcost,action,state,e1,e2,e3 );
% Costt=[Costt;cost];
% Episode=[Episode;k];
break
end
end
end
%% display the final Q matrix
vpa(Q,5);
[CC,I]=max(Q,[],2); % 给出Q table每一行的最大值存入CC,指标存入I
%% 根据Q-table取出最优策略
Action=[];
Path=[];
stMap = containers.Map('KeyType','int32','ValueType','any');
st_1 = zeros(AA,1)';
action_1 = action(I(1),:);
stMap(1) = st_1;
Path=[st_1;Path];
for i=2:T+1
demand=D(i-1,:);
st_1 = stMap(i-1);
% index_1 = find(ismember(state,st_1,'rows')==1);
state_key_sum1=strcat(num2str(i-1),num2str(st_1));
index_1 =state_Map_sum(state_key_sum1);
st_1 = st_1(:,1:AA); % the vector of the state
if i<=T
st_2 = st_1 - action(I(index_1),:) + demand; %next state
% index_2 = find(ismember(state,st_2,'rows')==1);
state_key_sum2=strcat(num2str(i),num2str(st_2));
index_2 =state_Map_sum(state_key_sum2);
action_2 = action(I(index_2),:);
stMap(i) = st_2;
Action=[Action;action_2];
Path=[Path;st_2];
elseif i==T+1
st_2 = st_1 - action(I(index_1),:) + demand;
% index_2 = find(ismember(state,st_2,'rows')==1);
state_key_sum2=strcat(num2str(i),num2str(st_2));
index_2 =state_Map_sum(state_key_sum2);
stMap(i) = st_2;
Path=[Path;st_2];
end
end
Action=[action_1;Action];
Path;
%% 根据最优策略算出成本
LC=Action*lcost;
Logcost=sum(sum(LC));
DC=createOC(Path(1:T,:),a,b,AA);
Depcost=sum(sum(DC));
TPC=createOC(Path(T+1,:),a,b,AA);
Oc=sum(sum(TPC));
Obj_Alpha=e1*Logcost+e2*Depcost+e3*Oc; % Qlearning 学习最终值
Obj_plot=repmat(Obj_Alpha,1,size(Episode,1))';
% profile viewer;
time=toc;
Obj_Alpha;
Objective_Alpha=[Objective_Alpha;Obj_Alpha];
end
OObjective_Alpha=[OObjective_Alpha,Objective_Alpha];
end
OObjective_Alpha
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
Lina Yu, School of Management and Engineering, Capital University of Economics and Business, Canrong Zhang, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen , Jingyan Jiang, Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, Huasheng Yang, Department of Industrial Engineering, Tsinghua University, Beijing, Huayan Shang, School of Management and Engineering,
[1]肖锋.基于强化学习的库位优化算法在物料拉动系统中的研究与应用[D].西南交通大学,2016.
[2]张烈卓.基于深度强化学习的云制造资源调度优化研究[J].[2024-03-24].






















 1088
1088

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










