二分法查找有序数组中的k所在的位置，互联网大厂笔试面试特别爱考的算法原型

数据结构与算法之二分法，互联网大厂笔试面试特别爱考的算法原型！

提示：二分查找系列文章
我们学习此题的目标除了理解二分法之外，还需要为下面两个题提供基础知识：
二分法查找有序数组arr中，大于等于k的最左侧、最右侧的位置
二分查找无序数组arr中的局部最小值的位置

---

题目

如果数组arr已经有序了，请你设计算法找到k所在的位置（下标）；
如果没有找到k的位置，则返回-1，代表没有找到；

---

一、审题

示例：arr=1 2 3 4 5 6 7 8 9 10，k=9；
找呗
从左往右遍历一下不就得了，

---

二、解题

显然，示例中的遍历方法，速度太慢，如果给你的N–>10^8，k也–>10的8次，你要遍历10**8次吗???
o(n)的算法自然不可取！！！

这时候咋办呢？

自然用二分法查找！
时间复杂度完全可以降到log(10^8)，我们知道210=1024=1000
那108<10^9=1000的3次方=2的10次方–的3次方
也就是2^30
注意：在数据结构与算法中，遇到log都是log以2为底的函数哦！！！记住了
那log(10^8)差不多<log(2**30)=30，显然这个速度，非常非常非常非常快！！！！

那么o(log(n))的算法复杂度怎么来的？？？
二分法的核心思想是什么？

（1）首先在L–R的升序数组上，寻找k所在的下标位置，我们完全直接直接去寻找L–R的中点mid
（2）如果mid所在的位置就是k，即arr[mid]=k，岂不是瞬间就找到了？返回mid就是结果；
（3）如果mid所在的位置那个数arr[mid]>k呢？由于arr有序，所以k必然在mid左边啊，下一次R直接变mid了，再回到（1）继续循环……
（4）如果mid所在的位置那个数arr[mid]<k呢？由于arr有序，所以k必然在mid右边啊，下一次L直接变mid+1了，再回到（1）继续循环……
（5）如果L>R了，不好意思一个没找到的话，那gg，返回-1，代表没有找到。
看图：

显然，如果你中点没有找到，自然下一次，根本不需要去另一半数组上找了，舍去大量的无效查找！！！
注意啊：舍去的思想，在算法中本质上类似于贪心策略，这是笔试题中75%的考题都会考到的贪心策略！！！
舍去的思想对于数据结构与算法来说，非常重要的，今后我们在看算法的过程中，慢慢体会啊！体会舍去的思想！！！

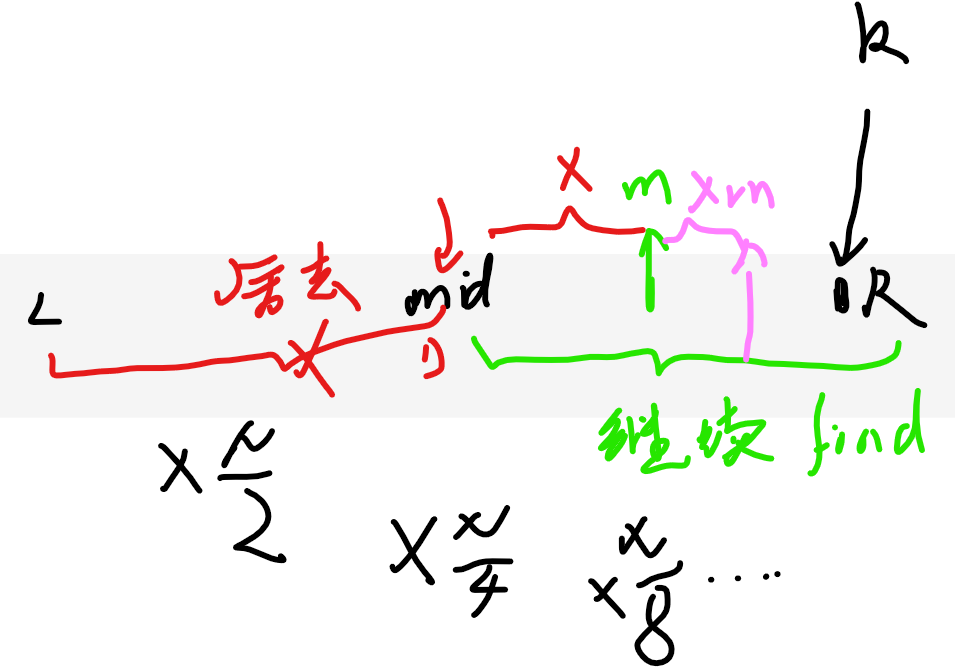
每一次舍去N/2的规模
下一次舍去N/4的规模
……
N/2^t
最多只需要t次一定能找到k

2^t=N的话，t次就是复杂度。
则只需要寻找o(log(N))次

手撕代码：

//最基础的二分法：
    //从L---R的有序数组上寻找k,返回k所在的位置，即下标
    public static int binaryFind(int[] arr, int L, int R, int k){
        while (L <= R){
            int mid = L + ((R - L) >> 1);//L--R的中点
            if (arr[mid] == k) return mid;
            else if (arr[mid] > k) R = mid;
            else {//arr[mid] < k
                L = mid + 1;
            }
        }

        return -1;
    }

注意！
这一句：int mid = L + ((R - L) >> 1);//L--R的中点
啥意思，就是(L+R)/2的意思
x>>1，x向右移位1位就是x/2的意思
x<<1，x向左移位1位就是2x的意思
1<<x，1向左移位x位就是2^x次方的意思；
**位运算，比四则±/快多了！！**
但凡在笔试面试过程中秀位运算的人，往往说明你的算法功底扎实！！！面试官会喜欢你的。

---

总结

提示：重要经验：

1）最基础的二分法，要理解，最开始犯糊涂没关系，后面熟悉了就行，多看两遍就知道了。
2）二分法是互联网大厂笔试面试经常考的东西，要熟练掌握！
3）位运算速度快多了！！！熟悉掌握，使用位运算有利于面试官给你印象分。