动手学深度学习 PyTorch 基础知识部分

1. 储备知识

1.1. 数据操作

创建一个行向量：x=torch.arange

获得张量的形状：x.shape

获得张量中元素总数（等于形状中所有元素的乘积）：x.numel()

改变张量的形状：reshape

使用全0初始化张量：torch.ones((2,3,4))

使用全1初始化张量：torch.zeros

随机初始化张量：torch.randn

使用列表初始化张量：torch.tensor([1,2])

运算符

具有相同大小的张量进行的操作是按元素运算（加减乘除，乘方，求幂等一元操作）

拼接concat((x,y),dim = k):

(3,4)(3,4) 0->(6,4) 1->(3,8)

判断两个张量是否相等：X == Y

对张量全部元素求和：X.sum()

广播机制

对于不同形状的两个张量，怎么进行逐元素操作：使用广播机制

会复制元素转换成新的数组，然后在对新生成的数组进行逐元素操作

索引与切片

一个多维数组X：X=torch.arange(12).reshape(3,4)

X[-1]:按第一个维度去取

X[m:n]：按第一个维度取出m到n-1的元素

指定索引写入元素：X[i][j]=num

为多个元素赋值：比如二位张量的第一行跟第二行重新赋值 X[0:1,:]=12

节省空间

需要原地操作：[:]或者+=，如果是x=x+y,那么位置就会改变

1.2. 读取数据集

import os

#os.makedirs("/data/d2", exist_ok=True)

absolute_path  =  "/data/huangxh/d2l-zh"
data_file = os.path.join(absolute_path, 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')  # 列名
    f.write('NA,Pave,127500\n')  # 每行表示一个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

import pandas as pd

data = pd.read_csv(data_file)
print(data)

该函数会把文件中的数据组织成一个格式的数据

首先先把输入分别处理了

对于int类型的列，将未知元素变为均值

把类别转换成类别元素判断

把分开的两个列再拼接到一起

inputs1,inputs2=data.iloc[:,0:1],data.iloc[:,1:2]
inputs1=inputs1.fillna(inputs.mean())
inputs2=pd.get_dummies(inputs2,dumpy_na=True,dtype=int)
inputs = pd.concat([inputs1,inputs2],axis=1)

把原先的格式去除掉默认的横纵坐标说明，只保留数据并转化成张量格式

inputs.to_numpy(dtype=float)
torch.tensor(inputs)

1.3. 线性代数

标量

初始化：torch.tensor(3.0)

向量

初始化：x = torch.arange(4)

找到对应的元素，使用下标： x[1] 表示x向量中的第二个元素

获取长度：len(x) 或者x.shape

矩阵

初始化：A = torch.arange(20).reshape(5,4)

访问其中某个元素：A[i][j]

转置矩阵：A.T

张量

初始化: X = torch.arange(24).reshape(2,3,4)

相同大小的张量的+，* 都是对应位置的元素进行操作的，并且不改变张量的形状

如果是把一个张量+或者* 一个常量，那么会对该张量中的所有元素进行操作

降维操作

对于一个张量A= torch.arange(20).reshape(5,4)

A.sum()会将所有元素相加返回tensor(190.)

如果想要在对应维度相加那么需要 A.sum(axis=0)

求平均值也可以进行降维：A.mean() 也可以指定维度A.mean(axis=0)

非降维求和

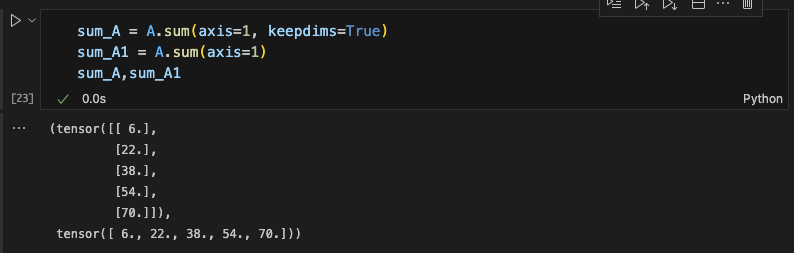
如果想要保持原先的形状，不降维，那么需要使用keepdims=True

点积

两个向量的点积：torch.dot(x,y)

或者逐元素相加，再求和：torch.sum(x*y)

矩阵乘向量

记得对应矩阵的第二个维度跟向量的大小相同

矩阵：A:m*n 向量 x: n torch.mv(A,x)

矩阵乘矩阵

矩阵：A: n* k 矩阵： B:k*m

torch.mm(A,B) 记得A的第二个维度跟B的第一维度相同

范数

L1范数：向量的绝对值之和 torch.abs(u).sum()

L2范数：向量的模 torch.norm(u)

1.4. 导数

偏微分

自动微分

想要计算梯度，x=torch.arange(4.0,requires_grad=True)

梯度就会储存在x.grad中

y = 2 * torch.dot(x,x)
y.backward()#反向传播更新梯度
x.grad == 4 * x

x.grad.zero_() #清除原先的梯度，不然会累加

如果希望把某些计算分离出计算图

比如 y = x * x , z = y * x 想要求z对x的梯度，但是希望把y作为一个常数，

y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x

非标量变量的反向传播

对于输出结果不是标量时，当想要调用向量的反向计算时，通常会试图计算一批训练样本中每个组成部份的损失函数的导数

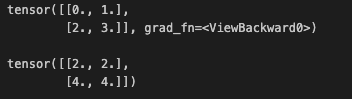
a = torch.arange(4.0,requires_grad=True).view(2,2)
c = torch.arange(4.0).view(2,2)
a.retain_grad()
b = torch.mm(c,a)

b.sum().backward()
print(c)
a.grad

对于上面这种需要转换形状的时候，原先是叶子节点，但是改变形状后就是非叶子节点，需要保留它们的梯度变回叶子节点。

此外对于这些结果，一般都是拿全部的求和然后对每个a中的元素进行偏导

课后习题

在运行反向传播函数之和再次运行它，会发生什么？

如果是默认情况，在第一个运行计算图之后，计算图就会被释放，所以第二次反向传播就会出错

如果想要多次使用，需要在反向传播中设置：z.backward(retain_graph=True)

为什么计算二阶导数比一阶导数的开销要大？

因为计算图需要迭代，计算二阶还要保存一阶的计算图，包括计算也更为复杂

在控制流的例子中，计算最终结果d关于输入a的导数，如果a从变量更改为随机向量或者矩阵，会发生什么？

1.5. 概率论

#给定分布概率
fair_prob = torch.ones([6])/6

#按上述概率随机取样一次
multinomial.Multinomial(1,fair_prob).sample()

输出结果就是相同与上面分布形状的出现次数

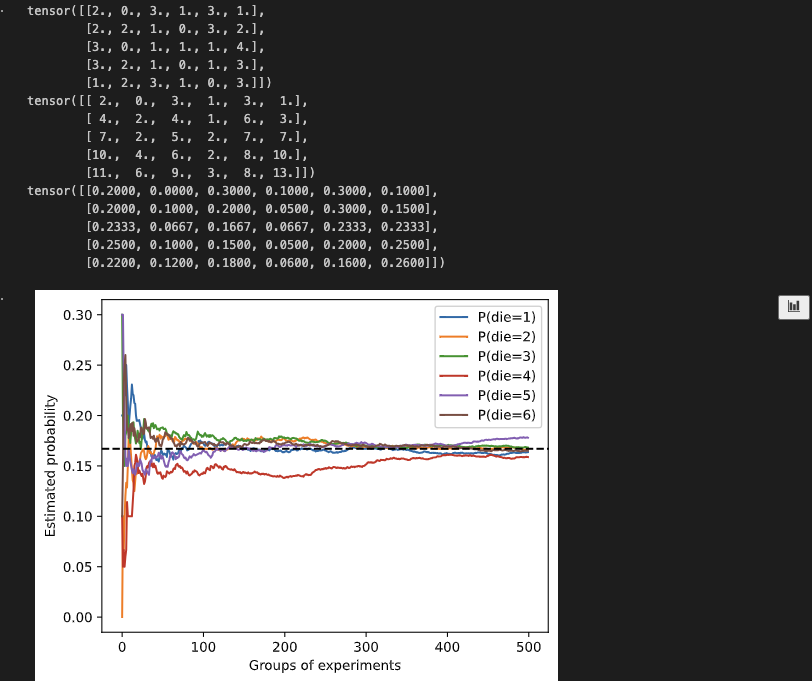
counts = multinomial.Multinomial(10, fair_probs).sample((500,))#模拟500组10次的投掷
print(counts[0:5,:])
cum_counts = counts.cumsum(dim=0)#随着次数增长，累计计算每个位置出现的次数
print(cum_counts[0:5,:])
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)#转化成概率，所以需要对于每行的总和，并且保持维度不变，这样才能对应相除
print(estimates[0:5,:])

d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].asnumpy(),
                 label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();