利用广度优先和深度优先算法解决迷宫问题【算法设计与分析】＜图搜索问题＞

实验问题：

给定一个n*n的迷宫，要求利用广度优先和深度优先算法解决迷宫问题

问题分析：

对于此问题首先要明确搜索顺序

可以分为两种方法求解问题：1.广度优先算法2.深度优先算法

（1）对于深度优先算法来说：<如果规定遍历顺序为下，右，上，左>

首先对于起始节点寻找其下节点，如果此节点能走，将其压入堆栈，并以此节点为准，在寻找其下节点，如果能走压入，不能走，就依次寻找右，上，左节点。直到找到最后一个节点即出口，将堆栈的值依次输出就是迷宫的路径。

（2）对于广度优先算法来说：<如果规定遍历顺序为下，右，上，左>

首先对于起始节点寻找其下节点，如果此节点能走，将其压入队列，并将起始节点压出队列。不能走就依次搜索右，上，左。直到找到最后一个节点即迷宫的出口。

数学建模：

开辟两个数组分别记录搜索顺序

用一个二位数组初始化迷宫，有墙处就是1，没墙处就是0，并归定不同的迷宫数组状态，maze[i][j]=0说明可以走；<maze[i][j]=1说明是墙;maze[i][j]=2说明无法继续 走;maze[i][j]=3说明已走>

依次按顺序搜索，搜索到一个节点就将其置为3，并依次顺序搜索这个节点的下，右，上，左节点。

当遇到无路可走且还未到终点时，将此节点值回复为0，并回溯到上个节点寻找解。

实验代码：

//采用深度优先算法解决走迷宫问题
//#define _CRT_NO_SECURE_WARNINGS
//
//#include<stdio.h>
//#include<iostream>
//
//using namespace std;
//
//int maze[8][8] = { {0,0,0,0,0,0,0,0},{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0} ,{0,1,1,1,1,1,1,0} };
//确定搜索顺序(下，右，上，左)
//int X[4] = { 1,0,-1,0 };
//int Y[4] = { 0,1,0,-1 };
//maze[i][j]=0说明可以走
//maze[i][j]=1说明是墙
//maze[i][j]=2说明无法继续走
//maze[i][j]=3说明已走
//
//打印路径
//void print() {
//	for (int i = 0;i < 8;i++) {
//		for (int j = 0;j < 8;j++) {
//			if (3 == maze[i][j]) {
//				cout << "A";
//			}
//			else {
//				cout << "-";
//			}
//		}
//		cout << "\n";
//	}
//	cout << "\n";
//	cout << "********"<<'\n';
//	cout << "\n";
//}
//
//void search(int i, int j) {
//	int x = 0;
//	int y = 0;
//	按照一个方向搜索到最后
//	for (int k = 0;k < 4;k++) {
//		x = i + X[k];
//		y = j + Y[k];
//		
//		搜索到可以走的结点
//		if (x >= 0 && x < 8 && y >= 0 && y < 8 && 0 == maze[x][y]) {
//			maze[x][y] = 3;
//			搜索到迷宫的最后一个结点即出口
//			if (7 == x && 7 == y) {
//				print();
//				maze[x][y] = 0;
//			}
//			else {
//				search(x, y);
//			}
//		}
//	}
//	若不成功回溯时将此节点置为0让其可以被其他路径访问
//	maze[i][j] = 0;
//}
//
//int main() {
//	maze[0][0] = 3;
//	search(0, 0);
//	system("pause");
//	return 0;
//}

//采用广度优先算法解决走迷宫问题
#define _CRT_NO_SECURE_WARNINGS

#include<stdio.h>
#include<iostream>
#include<vector>

using namespace std;

int maze[8][8] = { {0,0,0,0,0,0,0,0},{0,1,1,1,1,0,1,0},{0,0,0,0,1,0,1,0},{0,1,0,0,0,0,1,0},{0,1,0,1,1,0,1,0},{0,1,0,0,0,0,1,1},{0,1,0,0,1,0,0,0} ,{0,1,1,1,1,1,1,0} };
//确定搜索顺序(下，右，上，左)
int X[4] = { 1,0,-1,0 };
int Y[4] = { 0,1,0,-1 };
//maze[i][j]=0说明可以走
//maze[i][j]=1说明是墙
//maze[i][j]=2说明无法继续走
//maze[i][j]=3说明已走

struct sq {
	int x;
	int y;
	int pre;
};


void print() {
	for (int i = 0;i < 8;i++) {
		for (int j = 0;j < 8;j++) {
			if (3 == maze[i][j]) {
				cout << "A";
			}
			else {
				cout << "-";
			}
		}
		cout << "\n";
	}
	cout << '\n';
}

void mark(vector<sq>& q, int dex) {
	sq temp = q[dex];
	maze[temp.x][temp.y] = 3;
	//找到合适路径
	if (0 == temp.x && 0 == temp.y) {
		return;
	}
	//未找到路径回溯上一个节点
	else {
		mark(q, temp.pre);
	}
}
void search() {
	struct sq point;
	struct sq temp;
	int qh = 0;
	int qe = 1;
	point.x = 0;
	point.y = 0;
	point.pre = -1;
	vector<sq> q;
	int x = 0;
	int y = 0;

	//-1代表被访问过
	maze[point.x][point.y] = -1;

	q.push_back(point);
	//队列不为空
	while (qh != qe) {
		//节点出队
		temp = q[qh];
		qh++;

		//寻找下个节点可以走的地方
		for (int k = 0;k < 4;k++) {
			//按照一个方向搜索到最后
			x = temp.x + X[k];
			y = temp.y + Y[k];
			if (x >= 0 && x < 8 && y >= 0 && y < 8 && 0 == maze[x][y]) {
				//找到节点
				sq get_point;
				get_point.pre = qh - 1;
				get_point.x = x;
				get_point.y = y;
				//让其入队
				q.push_back(get_point);
				qe++;
				//找到迷宫的最后一个节点即出口
				if (7 == x && 7 == y) {
					mark(q, qe - 1);
					print();
					return;
				}
			}
		}
	}

}

int main() {
	maze[0][0] = 3;
	search();
	system("pause");
	return 0;
}

实验结果：

广度优先遍历：

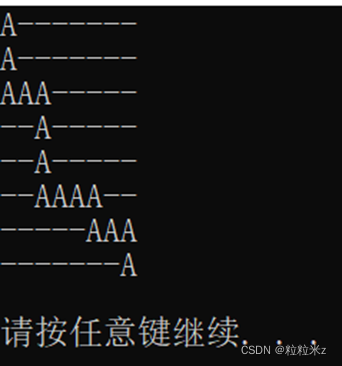
深度优先遍历： 

                                                                 

 时间复杂度分析：

最坏情况下：O（4(m*n-1)）（4为4个方向，m*n为迷宫空间）每个点都试探了一遍

最好情况O（min（m*n）-1）

算法的时间复杂度为O（2m*n）