行列式的计算(c++)——公式法（5阶）和递推法（n阶）

行列式的计算

行列式的众多正经的不正经的计算方法就属线性代数的内容了，这里不过多讨论，主要介绍代码中会用到的两种：

1. 公式计算
   行列式值的计算公式为
   $$\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \cdots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|=\sum _{p_1{p}_2\cdots p_n}(-1{)}^{\tau \left(p_1{p}_2\cdots p_n\right)}{a}_{1p_1}{a}_{2p_2}\cdots a_{n{p}_n}$$
   其中$\tau$是序列$p_1{p}_2{p}_3{p}_4\cdots$中的逆序对数且各$p_i$互不相同。
2. 利用代数余子式进行计算
   结论：行列式等于它任意一行(列)的各元素与其对应的代数式余子式乘积之和。
   $$\begin{array}{rl}\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|=& a_{11}\left|\begin{array}{cccc}{a}_{22}& a_{23}& \cdots & a_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n2}& a_{n3}& \cdots & a_{nn}\end{array}\right|-a_{12}\left|\begin{array}{cccc}{a}_{22}& a_{23}& \cdots & a_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n2}& a_{n3}& \cdots & a_{nn}\end{array}\right|+\cdots +(-1{)}^{1+n}{a}_{1n}\left|\begin{array}{cccc}{a}_{21}& a_{22}& \cdots & a_{2,n-1}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n1}& a_{n2}& \cdots & a_{n,n-1}\end{array}\right|\end{array}$$

1. 5阶矩阵行列式的计算

$$\left|\begin{array}{ccccc}{a}_{00}& a_{01}& a_{02}& a_{03}& a_{04}\\ a_{10}& a_{11}& a_{12}& a_{13}& a_{14}\\ a_{20}& a_{21}& a_{22}& a_{23}& a_{24}\\ a_{30}& a_{31}& a_{32}& a_{33}& a_{34}\\ a_{40}& a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right|=\sum _{j_0{j}_1{j}_2{j}_3{j}_4}(-1{)}^{\tau \left(j_0{j}_1{j}_2{j}_3{j}_4\right)}{a}_{0j_0}{a}_{1j_1}{a}_{2j_2}{a}_{3j_3}{a}_{4j_4}$$
C++代码实现

#include<iostream>
#include<string>

using namespace std;

int main()
{   
	double a[5][5] = { 0 };
	double result = 0;
	int j0, j1, j2, j3, j4, inverse, flag;

	//输入矩阵
	cout << "请输入矩阵的25个数据：";
	for (int i = 0; i < 5; ++i)
		for (int j = 0; j < 5; ++j)
			cin >> a[i][j];

	for (j0 = 0; j0 < 4; ++j0){
	 inverse = 0;                    //逆序对初值
	 for (j1 = 0; j1 < 4; ++j1){
		 if (j1 == j0)  continue;    //排除j1和j0相等的情况
		 else if (j1 < j0) ++inverse;//若j1<j0,则逆序数+1
		 for (j2 = 0; j2 < 4; ++j2) {
			 if (j2 == j0 || j2 == j1) continue;
			 inverse += (j2 < j0) + (j2 < j1);//若j2<j0 则（j2<j0)的值为1；若j2>j0 则（j2<j0)的值为0
			 for (j3 = 0; j3 < 4; ++j3) {
				 if (j3 == j2 || j3 == j1 || j3 == j0)continue;
				 inverse += (j3 < j2) + (j3 < j1) + (j3 < j0);
				 for (j4 = 0; j4 < 4; ++j4)
					 if (j4 == j3 || j4 == j2 || j4 == j1 || j4 == j0) continue;
				     //j4可以不利用枚举法
				     //j4 = 10 - j0 - j1 - j2 - j3;
				     inverse += (j4 < j3) + (j4 < j2) + (j4 < j1) + (j4 < j0);

					 flag = (inverse % 2 == 0 ? 1 : -1);
					 result += flag * a[0][j0] * a[1][j1] * a[2][j2] * a[3][j3] * a[4][j4];
			 }
		 }
	 }
	}
	for (int m = 0; m < 5; ++m) {
		for (int n = 0; n < 5; ++n)
			cout << a[m][n] << " ";
		cout << endl;
	}
	cout << "行列式的值是" << result << endl;
	return 0;
}

运行结果如下：
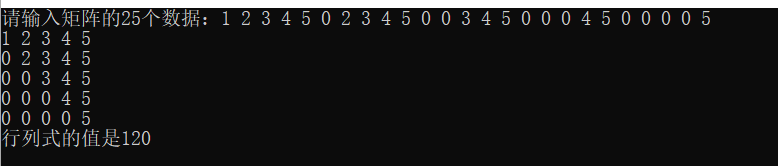注：为了能够简单验证结果的正确性，所以取的矩阵比较“好看”。

2. n阶矩阵行列式的计算

对于n阶矩阵来说，由于并不能在编程时确定其矩阵大小，上述方法则显得不是那么恰当，在这里利用指针构造动态数组进行计算。

动态数组和普通数组的最大区别在于，它的规模可以是运行程序过程种某一变量的值或某一表达式的计算结果，而普通数组的长度必须是在编译时就能确定的常量。

注：动态数组不能为数组元素赋初值

C++代码实现

#include <stdio.h>
#include <iostream>
using namespace std;

int det(int n, int** mat)//取矩阵的第一列进行运算
{
	int mov = 0;//记录a,b矩阵相对应的行数是否发生了改变
	int flag;
	int sum = 0;
	if (n == 1) return mat[0][0];
	int** b = new int* [n - 1];//创建第一列的n-1阶代数余子式矩阵
	for (int z = 0; z < n-1; ++z)
		b[z] = new int[n-1];//为每一行申请空间
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n - 1; ++j) {
			mov = i > j ? 0 : 1;
			//b中行数小于此时a中所取行数即i时，可直接将a中j行搬到b中j行；
			//b中行数大于此时a中所取行数即i时，需将a中第j+1行搬运到b中j行；
			for (int k = 0; k < n - 1; ++k)//开始一行一行的搬运
				b[j][k] = mat[j + mov][k + 1];//k+1是因为在搬运过程中不取mat中第一列
		}
		if (i % 2 == 0) flag = 1;
		else flag = -1;//判断符号的正负，因为所取值为mat[0][i],所以需判断1+1+i=i+2的奇偶
		sum += flag * mat[i][0] * det(n - 1, b);
	}
	delete[] b;
	return sum;
}
int main()
{
	int n = 0;//矩阵阶数
	cout << "输入矩阵阶数：" << endl;
	cin >> n;
	int** a = new int* [n];//所要求的矩阵,因为矩阵阶数不是常数，so不能直接创建数组，以指针的形式呈现。
	for (int z = 0; z < n; ++z)
		a[z] = new int[n];//为每一行申请空间
	cout << "输入矩阵：" << endl;
	for (int x = 0; x < n; ++x)
		for (int y = 0; y < n; ++y)
			cin >> a[x][y];
	for (int x = 0; x < n; ++x)
	{
		cout << endl;
		for (int y = 0; y < n; ++y)
			cout << a[x][y] << " ";
	}
	cout << endl;
	cout << "矩阵行列式的值为：" << det(n, a);
	for (int p = 0; p < n; ++p)
		delete[] a[p];
	delete[]a;
	return 0;
}

灵感来源于：https://blog.csdn.net/sinat_36219858/article/details/54016698
这篇博文并未利用二级指针，而是利用数组储存了全部矩阵信息。

运行结果如下：

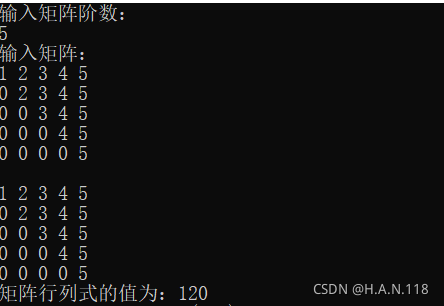
注：为了能够简单验证结果的正确性，所以取的矩阵比较“好看”。

当然，如果真的只是为了算个矩阵，仍旧强推MATLAB。

3. 踩坑记录

• 5阶矩阵的代码编写还是比较容易的，可以在此基础上进行改进，比如求个6阶，7阶也是可以的。
• n阶代码的确编了很长时间，可能是由于一学期不学线代+一学期不敲代码的原因，出了一些奇奇怪怪的错：

1. 循环的位置一定要看对，语句一定要放在正确的循环里。
2. 指针的基本操作要熟悉，要不不是忘了申请空间就是忘了释放空间
3. 行列要分清，不然。。。像我一样把 $mat[i][0]$写成$mat[0][i]$盯一下午？

• 顺便提醒一下，n阶的代码在VS上运行会报很多警告，大概是它跟多级2指针有仇，可以给大家看一眼：
  
  so，最后看不下去，用的codeblocks：
  
  距上一篇博客怕是已经半年了，这半年几乎没敲过代码（因为不上有关的课了）。下学期会学数据结构，so趁开学前几天把C++复习一下~