刷题笔记（十一）--栈和队列：Top-K问题

最新推荐文章于 2024-03-08 22:52:04 发布

梦想成为光头强！

最新推荐文章于 2024-03-08 22:52:04 发布

阅读量522

点赞数

分类专栏：刷题笔记文章标签：字符串 Top-k

本文链接：https://blog.csdn.net/weixin_53860901/article/details/124906967

版权

刷题笔记专栏收录该内容

23 篇文章

订阅专栏

系列文章目录

刷题笔记（一）–数组类型：二分法
 刷题笔记（二）–数组类型：双指针法
 刷题笔记（三）–数组类型：滑动窗口
 刷题笔记（四）–数组类型：模拟
 刷题笔记（五）–链表类型：基础题目以及操作
 刷题笔记（六）–哈希表：基础题目和思想
 刷题笔记（七）–字符串：经典题目
 刷题笔记（八）–双指针：两数之和以及延伸
 刷题笔记（九）–字符串：KMP算法
 刷题笔记（十）–栈和队列：基础题目

前言

这一部分呢，是针对于队列来说，因为TOP-K问题要用到这个，也就是优先级队列。老规矩，还是一点一点来。

$\color{red}什么是TOP-K问题？$

简单说一下，所谓TOP-K问题，就是在一份海量的数据中去寻找前K个最大或者最小的值。

可能会有人说，那我直接使用快排等排序算法不直接吗？这里注意一下，是海量的数据。如果说数据量不是很大，那么快排等排序算法当然是可以使用的。可是如果说数据量过大的时候，这个时候我们就要考虑的时候时间和空间的双重效率了，所以就要使用我们的优先级队列。

$\color{red}什么是优先级队列？$

所谓优先级队列，就是披着队列外衣的堆。优先级队列对外的接口只能是从队头取元素，从队尾加元素，所以从这一点来看它就是一个队列。而内部的元素就是自动依照元素的权值排列。

$\color{red}那么什么是堆呢？$

是不是好像有点越说越多了，

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

所以通俗一点，堆就是一棵完全二叉树的数组对象。

题录

215. 数组中的第K个最大元素.

题目链接如下:

215. 数组中的第K个最大元素

题目截图如下：
在这里插入图片描述
这道题就是一个基本的对于堆的掌握能力的考察，没有什么特别需要注意的地方，关于堆的构造我之前也写过相关的博客。

public class 数组中的第K个最大元素 {
    public int findKthLargest(int[] nums, int k) {
        int end = nums.length - 1;
        //总的思路就是构造一个大根堆，然后不停的删减元素，删除K个之后，此时的0号下标就是要求的
        for (int i = (end - 1) / 2; i >= 0; i--) {
            shiftDowm(nums,i,end);
        }
        //开始删减元素，删减K个之后就结束了
        while(k-- > 1){
            swap(nums,0,end);
            end--;
            shiftDowm(nums,0,end);
        }
        return nums[0];
    }

    public void shiftDowm(int[] nums,int parent,int end){
        //这里是定义的左孩子
        int child = parent * 2 + 1;
        while(child <= end){
            //首先要进行判断，父节点要和左右子树里面大的哪一个进行交换
            if(child + 1 <= end && nums[child] < nums[child + 1]){
                child = child + 1;
            }
            if(nums[child] > nums[parent]){
                swap(nums,parent,child);
                parent = child;
                child = parent * 2 + 1;
            }else{
                break;//如果说当前父节点的值大于子节点，那么就证明当前已经是大根堆，所以停止调整。
            }
        }
    }
    public void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

347. 前 K 个高频元素

题目链接如下：

347. 前 K 个高频元素

题目截图如下：

在这里插入图片描述

拿到这个题目的时候，第一反应就是用一个map的结构来存储键值对，然后根据键来对其进行排序。但是这里突然间没有一个很好的结构来储存排序中的这些键值对，最后没办法打开题解，发现看的有点懵，嗷~是好久没有看关于Map和Set的知识点了。所以这篇博客新加了一个复习篇章，就是复习一下我已经遗忘的知识点。

public class 前K个高频元素 {
    public int[] topKFrequent(int[] nums, int k) {
        //首先定义一个Map用来存储每个元素和其出现的顺序
        Map<Integer,Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int key = nums[i];
            map.put(key, map.getOrDefault(key,0) + 1);
        }

        //然后把这些映射关系全部返回,用一个set接收起来
        Set<Map.Entry<Integer,Integer>> sets = map.entrySet();
        PriorityQueue<Map.Entry<Integer,Integer>> minQue = new PriorityQueue<>(
                //其实这一行是完全可以省略的，因为优先级队列本来就是默认小根堆
                (o1,o2) -> (o1.getValue() - o2.getValue())
        );
        //然后就是遍历所有的映射关系，根据值来进行堆排序。
        for(Map.Entry<Integer,Integer> set:sets){
            minQue.add(set);
            if(minQue.size() > k){
                minQue.poll();
            }
        }
        int[] arr = new int[k];
        //然后堆当中剩余的键值对一个一个往出删，删一个存一个的key
        for(int i = k - 1;i >= 0;i--){
            arr[i] = minQue.poll().getKey();
        }
        return arr;
    }
}

所以这道题在熟悉Map操作的基础上，还是很容易做出来的。

复习

<1>关于比较器

这个部分的书写是因为发现自己对于大根堆和小根堆的建造，印象很模糊很模糊了。（十分钟后）笔者这会已经感觉自己对之前的知识遗忘的很厉害，为啥呢，就是笔者之前第一次在了解关于比较器的知识点的时候是在String类这部分的时候，然后复习着复习就感觉情况不那么简单，确实有些知识点遗忘了。

1.关于CompareTo

这个知识点其实就是笔复习时候发现的，就先使用这个知识点引申出以下的内容。

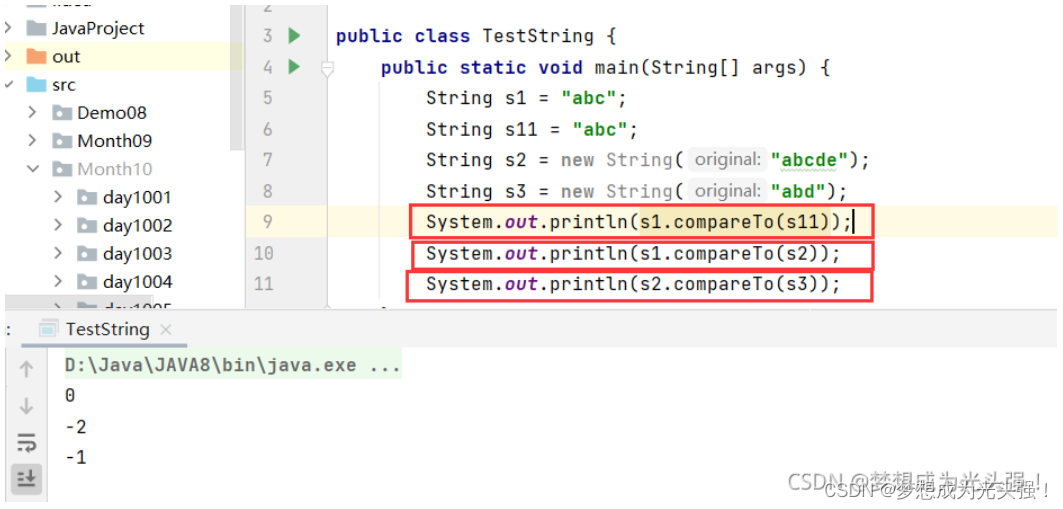
在这里插入图片描述

红框一：两个字符串相同，返回0
红框二：一个字符被另一个字符包含，返回两个字符串的长度差值
红框三：两个字符串不同，返回两个字符串中第一个不同字符的字典序差值。注意：字典序差值！字典序差值！字典序差值！！

2.关于Comparable和Comparator

这两个都是用来实现元素排序的，但是二者还是有着很本质的区别的。

$\color{red}1.字面含义$

Comparable是“比较”的意思，而Comparator是比较器的意思。前者是able结尾，也就是说它自身就有这着某种能力，而后者是or结尾，表示自己是比较的参与者。

$\color{red}2.用法不同$

他们都是顶级的接口，但是所有的方法和用法是完全不同的。

Comparable用法：此接口只有一个方法，就是ComparaTo，实现Comparable接口并且重写CompareTo方法就可以实现某个类的排序。它支持Collections.sort和Arrays.sort的排序。
CompareTo方法说明：此方法接收的参数P是要比较的对象，就是用当前的对线和要对比的对象进行比较，然后返回一个int类型的值，正序从小到大的排序规则是【使用当前对象的值减去要对比的对象的值】，倒序从大到小的排序规则是【使用要比较的对象的值减去当前对象的值】。当然了，如果说当前类没有继承Comparable接口，那么就不能使用Collection.sort方法进行排序。

Comparator用法：当前接口的实现排序的方法不是CompareTo，而是Compare
拓展Comparator匿名类：Comparator除了可以通过创建自定义比较器外，还可以通过匿名类的方式，更快捷，便捷的完成自定义比较器的功能。

$\color{red}3.使用场景不同$

1.如果说要使用Comparable接口，就必须要修改原有的类，也就是你要排序的那个类，就要在那个类中实现Comparable接口并且重写CompareTo方法，所以从这点来看Comparable接口更像是“对内”进行排序的接口。
2.Comparator则不需要修改原来的类，也就是说即使这个类是第三方提供，我们依然可以通过创建新的自定义比较器Comparator来实现对第三方类的排序功能。也就是说通过Comprartor接口可以实现和原有类的解耦，在不修改原有类的情况下实现排序功能。所以从里来看Comparator可以看作是“对外”提供排序的接口。

<2>关于map的复习

这一部分的复习内容是笔者在看题解的时候，发现自己对于map的方法有了很大的遗忘，所以这一部分在这里也复习一下。

1.什么是map

map是一个接口
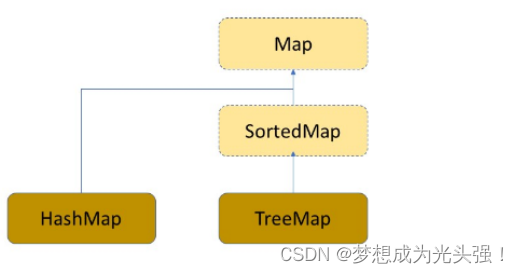
在这里插入图片描述
可以看到，该接口并没有继承Collection。该类存储的是键值对<K,V>，并且key一定是唯一的，不能重复。

2.关于Map.Entry(K,V)

Map.Entry(K,V)是Map内部实现的用来存放<key,value>键值对映射关系的内部类。该内部类主要提供了关于<key,value>的获取方式，以及key的比较方式等等。常用的方法有如下：
在这里插入图片描述
这里的话主要是这个Set<Map.Entry<K, V>> entrySet()不是很好理解，所以可以对应着我们上面的347题理解。然后对于这些还有一些地方需要说明的

1.Map是一个接口，不可以直接实例化对象，只能实现其实现类TreeMap或者HashMap
2.key唯一并且不能为null，但是value可以为空也可以重复
3.Map中的key可以全部分离出来存储在set中。（key不可重复）
4.Map中的value可以全部分离出去，存在Collection的任何一个子集合中（value可能重复。）
5.value可以修改，但是key不能修改，如果要改只能删除后再插入。