引子
去年春节假期在老家写的一个小文章,节后M10、华仔还有宋程帮忙做了些补充和完善。投稿过程一波三折,被拒稿两次。第一次被拒稿原因是说我这个不是科学研究。第二次被拒审稿人可能觉得我的内容很多不忍心,写了几百字推介了论文的标准格式应该怎么写,在此表示感谢。文章最后发表在北京交通工程学会主办《交通工程》杂志2023年第六期。
最近几年的习惯,有想法就做个模拟实验来验证,我想实验应该算是一种科学的研究方法。回到这个论文的主题,最初的设想是想验证OD估计是否过程可逆,然后有了这个先验实证。成稿的时候和Nature讨论,被鄙视说我戳自己轮胎。当然,关于Nature所说的文章容易被断章取义让人造成不可信的误解,这个观点我也是非常认可的。
关于OD估计这个问题,初始矩阵的质量是基础,需要重视研究方法的适用条件是我想表达的观点,研究技术方法的适用条件应该也是有意义的工作。OD估计是行业最基本的通用工具方法,关于适用条件的讨论也相对比较少见。在做这个文章之前我也只是猜想,没有想到结果会这么极端,将结果做个分享是希望能大家能重视这件事情,题目用问句也是这个考虑。
大数据时代带来了很多的改变,也让我们更加接近真相。从小样本到大样本,数据基础本身也有质的改变。通过一个接近上帝视角来审视传统建模方法可能存在的问题并寻找改进方向应该是一件非常值得去做的事情,也可能是寻找理论创新的突破点,毕竟现在国内的数据条件应该是全球独一无二的。当然,审视不是为了否定,而是为了寻找更加正确的方向。
摘要
围绕OD矩阵估计技术是否能够还原真实OD这一问题,设计了基于仿真实验的研究方法进行实证研究。大型网络交通模型和小型网络交通模型的研究结果均显示初始输入矩阵是OD估计技术可用性的关键,且对大型交通模型来说构造初始矩阵法近乎失效;路段流量模拟值与观测流量的相关系数不能保证结果的可靠性;考虑转向交通流量的强约束条件下,小型交通模型OD估计结果在观测流量、GEH值等指标上表现近乎完美,但与真实矩阵之间仍存在一定差异。总之,OD估计技术能够发挥一定的实践作用但并不完美,追求高质量的初始OD矩阵是该技术有效应用的关键所在。
0 引言
OD估计(OD matrix estimation, ODME),又称OD反推,是指利用调查和时空位置挖掘等方法得到的初始OD矩阵基于观测交通流量推断更可信出行OD矩阵的技术,是交通需求建模过程中最基础的技术方法,被广泛应用于交通规划、交通运行评估等工程实践。在数据库Taylor & Francis Online中检索摘要中包含“OD matrix estimation”关键词,文章超过5900篇。在数据库CNKI中检索摘要中包含“OD估计”或“OD反推”的学位论文及期刊论文约有900篇,由此可见该项技术方法的广泛影响。OD矩阵估计也是各类交通工程学科教科书的交通需求推算方法, Ortuzar和Willumsen编著的经典交通模型教材《Modelling Transport》[1]第12章第4节是关于OD矩阵估计数学模型的专门介绍。此外,主流交通模型商业软件TransCAD、EMME、CUBE、VISUM、AIMSUM和SIAS Paramics等均提供了通用的OD估计功能。从求解方法来看,商业软件主要采用的了数学优化方法,VISUM的TFlowFuzzy模块算法源自Van[2]提出的最大似然估计,EMME软件采用Spiess[3, 4]所提出的梯度法和最大似然估计,TransCAD软件采用的是Nilsen[5]提出的双层优化模型,Cube 软件采用的是最大似然估计[6]。从求解输入条件来看,主要包括初始矩阵、核查线观测点交通量及允许误差范围、交通小区产生吸引量的允许误差范围等指标。从检验方法来看,主要是观测值和模拟值的相关性分析及拟合优度(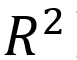 )以及观测点/核查线的误差。从检验标准来看,通常参考英国路桥设计手册[7]第12卷所采用的检验标准,该标准根据观测点交通量大小设置了不同交通流量范围对应的容许误差,并规定了核查线的误差范围5%。此外,为了降低交通量绝对值差异带来的影响,该标准中还采用了GEH[8]指标及其检验标准,并从观测点、核查线等方面给出了建议值。本文的研究问题是:在校核流量模拟值和观测值能够很好的满足相关检验标准的条件下,估计结果能否代表真实OD矩阵?本文将尝试通过模拟实验的方法对该问题予以解答。
)以及观测点/核查线的误差。从检验标准来看,通常参考英国路桥设计手册[7]第12卷所采用的检验标准,该标准根据观测点交通量大小设置了不同交通流量范围对应的容许误差,并规定了核查线的误差范围5%。此外,为了降低交通量绝对值差异带来的影响,该标准中还采用了GEH[8]指标及其检验标准,并从观测点、核查线等方面给出了建议值。本文的研究问题是:在校核流量模拟值和观测值能够很好的满足相关检验标准的条件下,估计结果能否代表真实OD矩阵?本文将尝试通过模拟实验的方法对该问题予以解答。
1 模拟实验方案总体设计
考虑实践应用中不同规模的交通模型结果校核方法差异和初始矩阵获取途径不同等因素,模拟实验分为两种情形:大型网络模型和小型网络模型。大型网络模型主要面对城市级交通模型,校核检验对象是核查线;小型网络主要面向小区域的详细路网模型,除校核线之外还将考虑主要交叉口转向交通流量作为约束,可以理解为强约束条件的OD矩阵估计。此外,考虑获取真实的OD矩阵极为困难,本文采用基于卡口数据推断的初始OD矩阵并利用OD估计技术,建立能够较好适配实际交通运行状况的OD矩阵作为目标矩阵,并用此矩阵分配所得路段/转向交通流量作为虚拟观测值,以此为基础开展模拟实验。截止2021年9月,广州市常态卡口数量7901个,其中能够进行有效数据采集的5653个,并对车牌脱敏后的卡口数据形成了固定采集和分析机制,按月度进行数据清洗和分析,能够获得相对较高质量的车辆初始OD矩阵。
初始矩阵质量对校核结果也有较大的影响。实践中,初始矩阵的获取方法通常包括常数矩阵法和重力模型法,可以看作是构造矩阵。常量矩阵法是指将具备通行条件的所有OD对之间的出行量置为常数,例如取值为10;重力模型法是根据交通小区的产生和吸引量,结合多源数据获取的广义出行距离分布作为约束,进行出行分布参数标定,并计算得到初始OD矩阵。为进一步验证初始矩阵质量对校核结果的影响,以目标矩阵分别乘以误差范围在和范围内的均匀分布随机误差作为高质量、低质量初始矩阵开展后续检验。
实证检验包含观测值检验和目标矩阵检验。观测值检验主要是估计矩阵分配后的观测点流量模拟值与实际观测值的相关性检验及GEH指标检验。目标矩阵检验是OD估计结果矩阵和先验的目标矩阵之间的对比,包括相关性、误差、出行距离分布变化等。本文实验采用PTV VISUM 2022版作为软件实验平台。为增加不同OD矩阵分配结果的可比性,交通分配中的道路速度-流量函数采用标准BPR函数(式1),即不考虑转向交通延误等分配计算过程中的新变量影响。考虑流量观测点的位置和数量对校核结果也会有较大的影响,本研究重点研究的是方法的有效性,基于合理的观测点位置及合适数量规模开展。实验流程方案见图1所示。
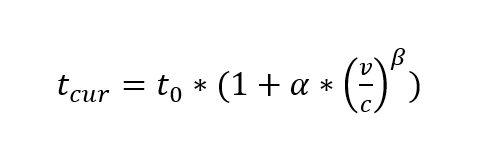 (式1)
(式1)
式中:
——分别是路段自由流通行时间和当前状态通行时间
——路段流量
——路段通行能力
——模型参数,本文中取值如下

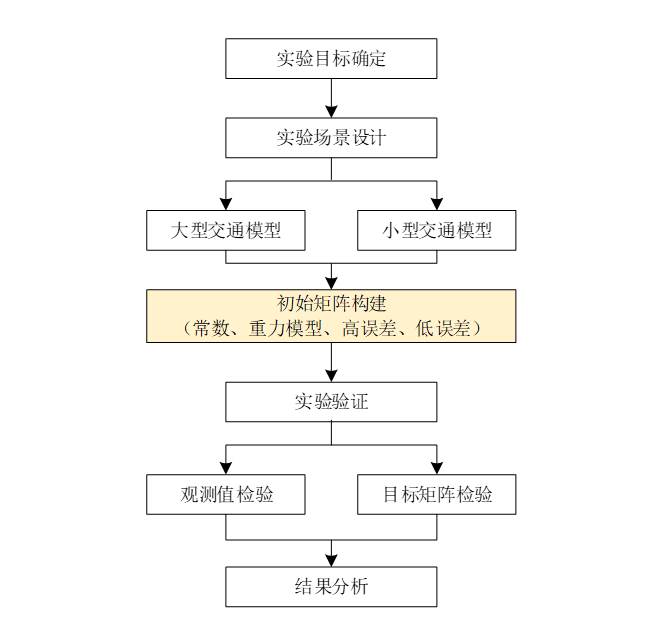
图1 实验总体流程
2 大型网络交通模型模拟实验
2.1 基础模型概况及OD矩阵估计方案设定
本次实验采用的大型网络模型为广州市中心区范围约340平方公里的范围(见图2),共包含1411个交通小区,6797个节点和13413个可通行路段。结合道路网络结构,共设置核查线60条,覆盖了826个单向道路断面,目标矩阵出行总量为420243pcu/h。
按照实验设计,分别构造常数矩阵、重力模型、高误差和低误差四个初始矩阵作为输入,路段观测点和交通小区产生吸引量的允许误差条件见表1。同时考虑实践应用中有时会添加OD矩阵的出行距离分布作为约束条件,本文也设置了重力模型初始矩阵叠加出行距离分布的情形,总计五种实验情形进行对比分析见表2。
表1 路段观测点和交通小区产生吸引量允许误差条件

表2 大型网络交通模型OD估计实验情形

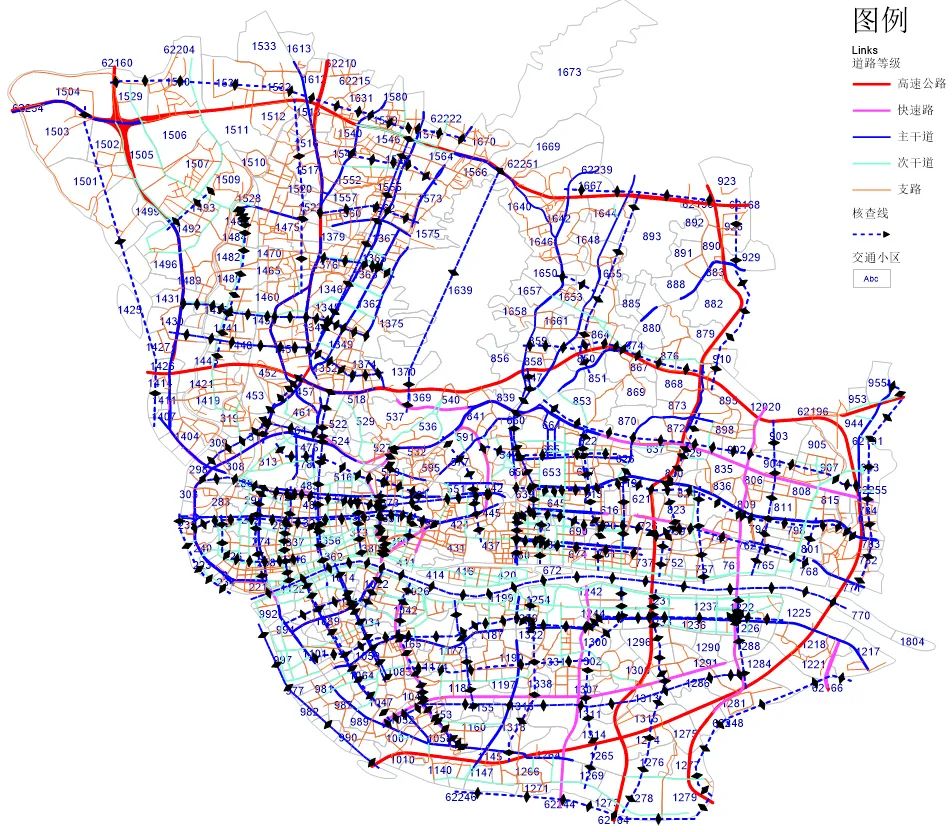
图2 大型网络交通模型交通分区、路网和核查线示意图
2.2 模拟测试与观测值检验
1)总体指标
运用VISUM 2022版的TFlowFuzzy模块进行前述五种实验情形的OD矩阵估计,总体情况见表3所示。从模型迭代次数和耗时指标看,整体呈现初始矩阵质量越高,迭代次数和耗时越少的趋势,且出行距离分布约束条件的引入会显著增加迭代计算次数和运行耗时。从结果误差来看,情形一需求总量变化最大,误差约达8.9%,其次为情形二,约0.68%,其它三种情形误差均小于0.03%,能够较好匹配目标矩阵的总需求量约束。需要说明,本次实验中由于情形一的出行需求总量偏差较大,实验中尝试将该情形的OD矩阵估计结果作为输入,代替常数矩阵进行分析,能够得到与重力模型相似精度的结果,但为了对比的公正性,这里仍然使用常数矩阵直接OD估计结果作为方案比较。
表4 总体测试效率效果指标表

2)核查线观测值点检验
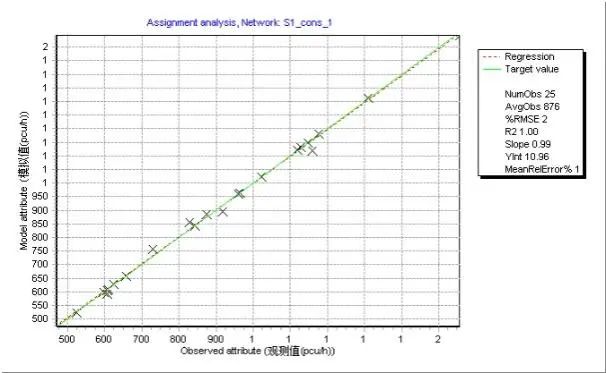
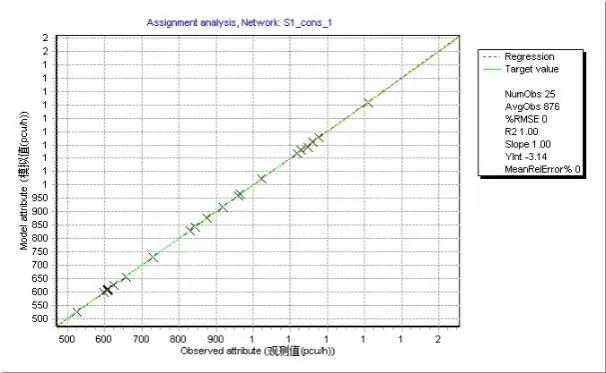
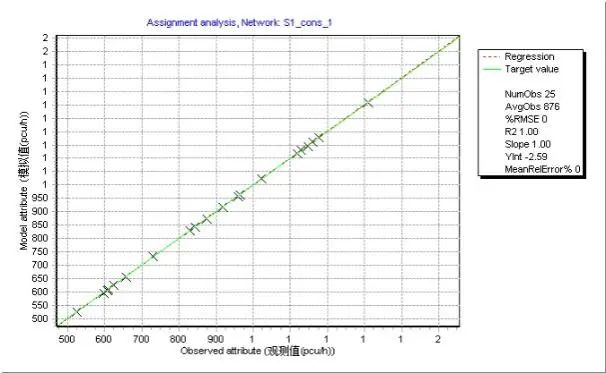
将OD矩阵估计结果进行交通分配,五种情形下路段流量的模拟值与观测值均呈现很强的线性关系,拟合优度( )均达到0.99以上;但从GEH检验标准来看,五种情形的实验结果呈现一定差异性(见表5)。常数初始矩阵情形下GEH值小于5的点位数仅为434个,占比约52.5%。以重力模型初始矩阵的两种情形GEH值小于5的点位数占比均超过85%,能够满足检验要求。情形四和情形五的模拟值能够近乎完美复现流量观测值,且所有观测点流量的GEH值均小于2。分析结果表明,即便模拟值和观测值的线性拟合优度达到0.99,也存在GEH值检验不满足要求的情况,提醒实践应用中有必要采取更为完备的检验方法。
)均达到0.99以上;但从GEH检验标准来看,五种情形的实验结果呈现一定差异性(见表5)。常数初始矩阵情形下GEH值小于5的点位数仅为434个,占比约52.5%。以重力模型初始矩阵的两种情形GEH值小于5的点位数占比均超过85%,能够满足检验要求。情形四和情形五的模拟值能够近乎完美复现流量观测值,且所有观测点流量的GEH值均小于2。分析结果表明,即便模拟值和观测值的线性拟合优度达到0.99,也存在GEH值检验不满足要求的情况,提醒实践应用中有必要采取更为完备的检验方法。
表5 不同情形下的观测点流量模拟值与观测值的检验
情形 | 模拟值与观测值对比分析 | GEH检验及拟合优度 |
|---|---|---|
情形一 |
| GEH<5共434个,占比52.5%,不满足检验要求; |
情形二 |
| GEH<5共716个,占比86.7%,满足检验要求; |
情形三 |
| GEH<5共712个,占比86.2%,满足检验要求; |
情形四 |
| GEH<5共826个,占比100%,且所有GEH值均小于2,满足检验要求; |
情形五 |
| GEH<5共826个,占比100%,且所有GEH值均小于2,满足检验要求; |
2.3 目标矩阵检验
前一节对路段观测点流量数据的拟合精度进行了检验,拟合优度()接近于1,而GEH值检验除情形一外均能够满足要求。但路段观测点流量误差检验合理是否就意味着OD矩阵也满足要求,需要进一步验证。
1)OD对之间出行需求检验
各情形OD矩阵估计结果的出行需求与目标矩阵的比较结果呈两级分化态势(见表2)。基于纯构造初始矩阵的实验情形一、二和三的结果较为接近,OD对之间的出行需求与目标矩阵拟合优度较差(图3),最高仅为0.376;而通过目标矩阵设置随机均匀误差生成初始矩阵的情形四和情形五呈现较高质量的估计效果,估计结果能够较为显著的减少误差,这表明初始矩阵的质量是影响OD估计结果的关键变量。
表6 不同情形估计OD矩阵和目标OD矩阵OD对拟合优度表
情形 | 情形一 | 情形二 | 情形三 | 情形四 | 情形五 |
拟合优度 | 0.311 | 0.376 | 0.374 | 0.98 | 0.996 |
|
|
| b情形二 |
| |
c情形三 |
图3 情形一、二、三OD估计矩阵和目标矩阵比较
|
|
a情形四初始矩阵 | b情形四OD估计矩阵 |
|
|
c情形五初始矩阵 | d情形五OD估计矩阵 |
图4 情形四和情形五初始矩阵及OD估计矩阵与目标矩阵比较
2)出行距离分布检验
如图5所示,在不增加出行距离分布约束的条件下OD估计结果会产生出行距离分布的变化。情形一和情形二出行距离分布显著偏离目标OD矩阵,而情形三通过设置出行距离分布约束条件能够复现目标出行OD矩阵的出行距离分布形态,但未发现出行距离分布的约束对提升OD估计结果精度的积极作用。

图5 出行距离分布比较
2.4 小结
大型交通模型的OD矩阵估计实验表明,现有成熟应用的OD矩阵估计方法能够实现模拟值对观测值高质量的拟合,但不能仅依靠观测点流量结果的拟合优度作为检验标准,需要进一步开展GEH值计算以确保模型校核精度和提升估计结果质量。路段模拟值和观测值的匹配并不一定意味着OD矩阵估计结果能够真实反映实际出行OD。初始矩阵的质量是OD估计模型的关键,通过构造矩阵法生成的OD矩阵作为初始矩阵并不能保证获得高质量的估计结果。脱离原始数据和多源的实际检验数据,完全依赖构造矩阵来推断OD矩阵即便与观测值存在良好检验关系也可能存在显著偏差和误导。
3 小型网络交通模型模拟实验
3.1 基础模型概况及OD矩阵估计方案设定
小网络模型(图6)包含8个交通小区,20个节点和20个路段。交通运行数据包含14个路段共25个方向的路段交通量观测数据以及研究范围内全部5个交叉口共38个转向交通流量数据(见图7),出行需求总量为5994pcu/h。与大型网络模型通过核查线及观测点流量来开展研究不同,小型网络的OD估计模拟实验还增加了转向交通流量作为约束条件,从路段观测值发展到路段加转向观测值,提升了约束条件的层次性。同时增加了转向交通流量的误差检验,能够更进一步的检验OD估计结果与观测数据的最佳适配。
大型网络交通模型中已经对路段观测点校核方法进行了研究,结果表明初始矩阵的质量是OD矩阵估计结果正确性的关键变量,同时考虑以目标矩阵生成的两种矩阵校核结果差异较小,本节只研究对低误差初始矩阵情形。按照实验设计设想,使用常数矩阵、重力模型和与目标矩阵存在低随机误差三个矩阵作为初始矩阵,并按照有无交叉口转向流量作为约束条件,构造六种情形(见表7),误差条件同表1。与大型网络交通模型相比,由于小型网络的交通模型的运行速度快,时间近乎可以忽略,因此不考虑运行速度和迭代次数等效率等指标的对比评价。
表7 小型网络交通模型OD估计情形设定
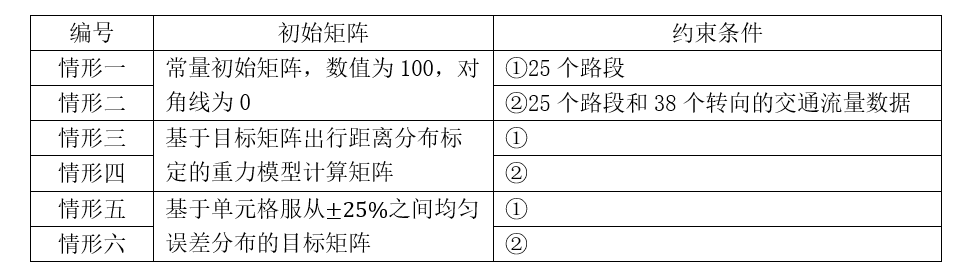
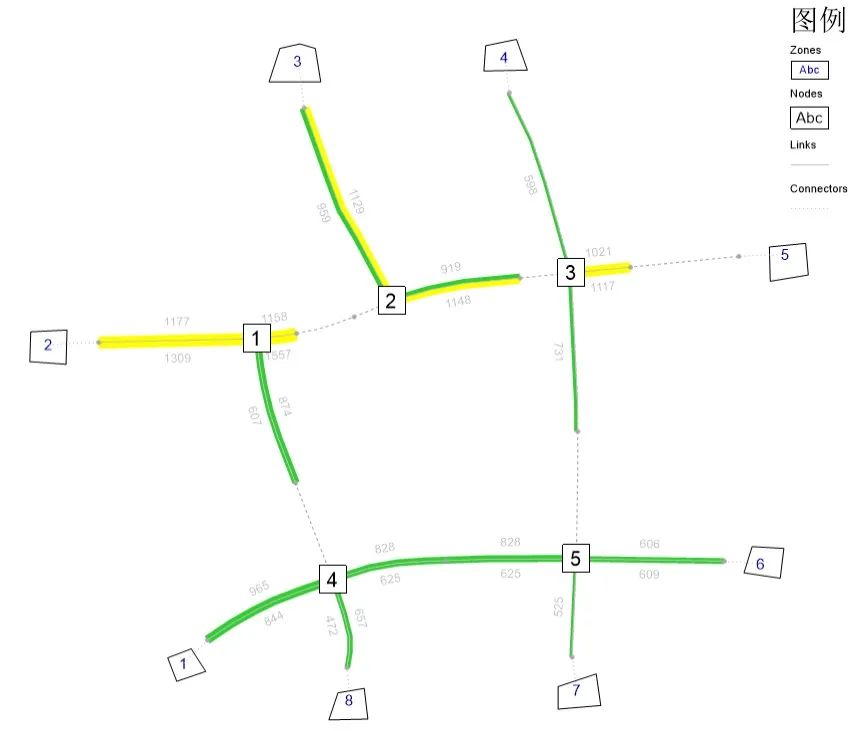
图6 交通网络、交通分区与交叉口编号示意
|
|
|
|
|
图7 交叉口流量流向图
3.2 观测值检验
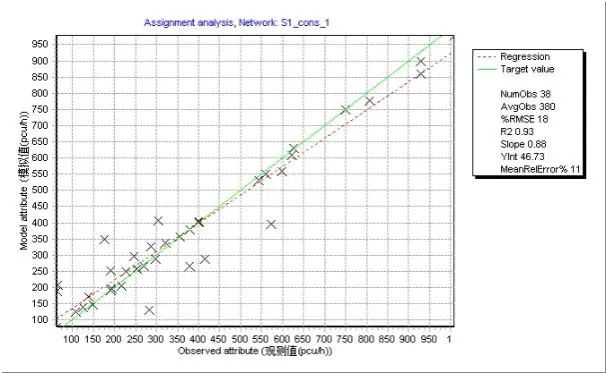
1)路段交通量检验
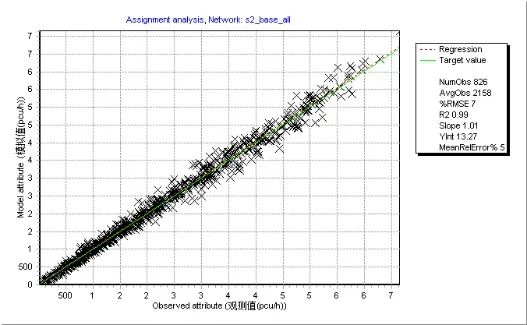
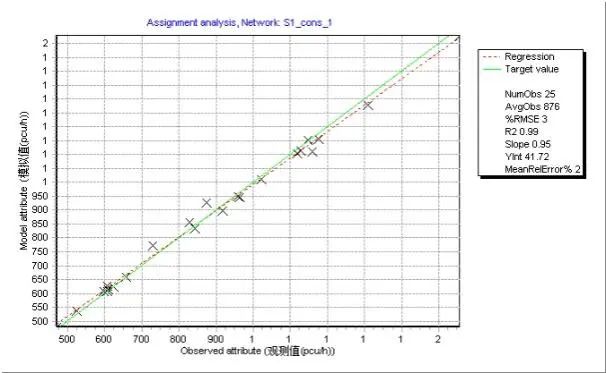
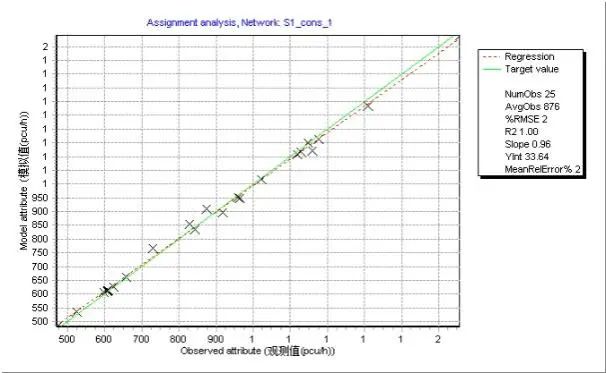
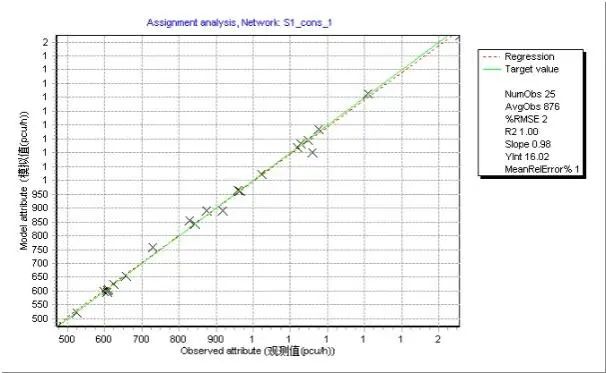
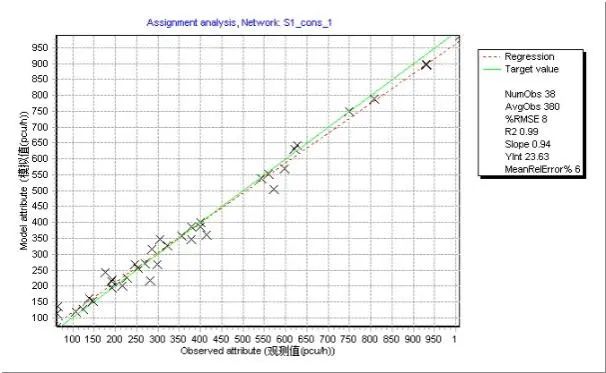
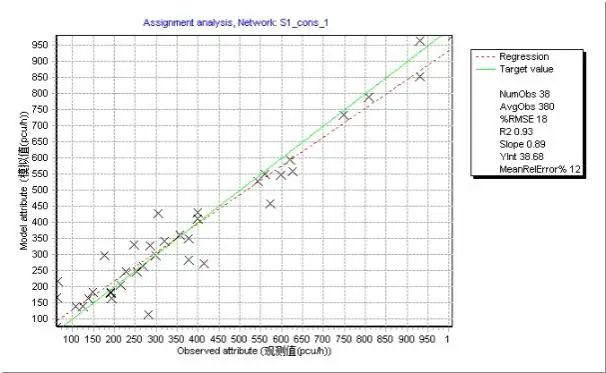
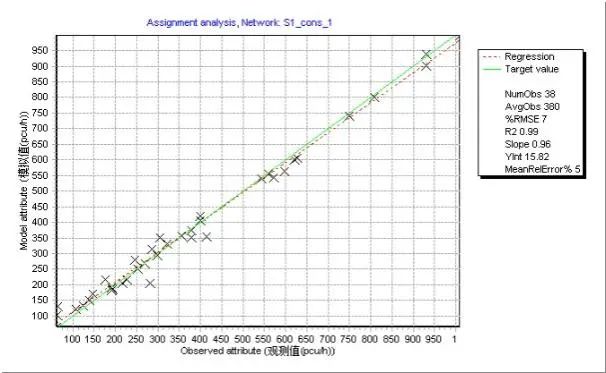
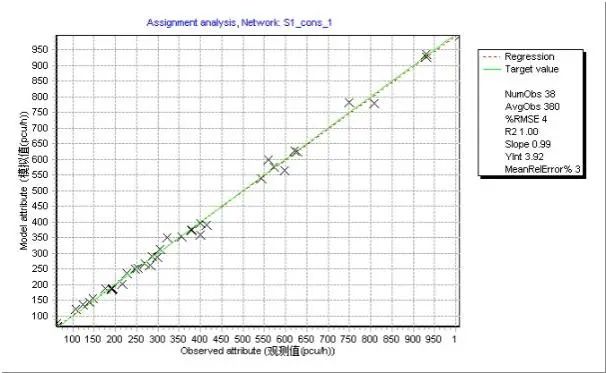
同大型交通模型的实验方法,对六种情形进行检验。总体来看,转向交通约束条件能够有效提升校核质量(见图8),有助于改善拟合优度并减少相对均方根偏差(RMSE)。
|
|
a情形一 | b情形二 |
|
|
c情形三 | d情形四 |
|
|
e情形五 | f情形六 |
图8 路段交通量观测值与模拟值比较
2)转向交通量检验
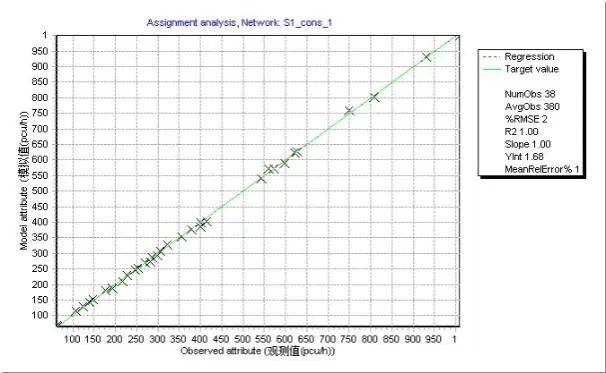
路段流量的校核精度和交叉口转向交通量的模拟精度有一定独立性,未考虑转向流量约束条件的校核结果,其转向交通流量误差显著(见图9),这也说明仅考虑路段流量约束的校核结果对路网的真实OD估计存在不足。
|
|
a情形一 | b情形二 |
|
|
c情形三 | d情形四 |
|
|
e情形五 | d情形六 |
图9 转向交通量观测值与模拟值比较
3.3 目标矩阵检验
从矩阵校核结果来看,OD矩阵的估计结果与目标矩阵的拟合优度较高(见表8),且考虑交叉口转向流量约束条件下估计结果更为准确(见图10)。参考核查线观测点的检验标准,考虑交叉口转向流量约束条件的OD估计结果中GEH值小于5的OD对占比均超过85%,满足检验条件。但前四种以构造矩阵为初始输入矩阵的估计结果与目标矩阵相同OD点对的变化来看,依然偏差明显。从矩阵总量来看,OD对的绝对误差之和的最小值为16.3%。从OD对来看,平均误差最小值为38.5%,中位数为16.7%,也表明估计的OD矩阵与目标矩阵存在较明显的差异。与之对比,情形五和情形六的结果再次验证了改善初始输入矩阵是提升OD估计结果的优选途径,在拟合优度、绝对误差比、平均误差和误差中位数等指标方面均有较好的表现。
表8 OD估计结果评价

注:
①OD对绝对误差求和/目标矩阵求和
②OD对误差绝对值除以目标矩阵对应元素的平均值
③OD对误差绝对值除以目标矩阵对应元素的中位数
|
|
a情形一 | b情形二 |
|
|
c情形三 | d情形四 |
|
|
e情形五 | d情形六 |
图10 OD估计矩阵与目标矩阵的比较
3.4 小结
小型网络交通模型的模拟实验表明,以构造矩阵作为初始输入且仅考虑路段流量观测值作为约束条件的OD估计结果存在较明显不足,不宜作为目标矩阵。在考虑交叉口转向流量约束条件下,OD矩阵估计结果虽然能够满足GEH值检验的要求,但仍不能否认其与目标矩阵的差异,模拟实验再次验证了改善初始输入矩阵质量是提升OD估计结果精度的关键。文中算例是超强约束条件下的求解结果,模型中包含43个有效OD点对,约束条件包括25个流量观测断面(单方向)、38个转向流量以及交通小区的14个产生或吸引量,总计77个约束条件,平均每个变量对应1.8个约束条件。这也意味着尽可能挖掘更多的观测值作为约束条件是提升模型精度的关键技术路径。
4 结语
根据Willumsen[9]的描述,最早的OD估计模型始见与1972年[10],距今已超过50年。在这半个世纪的时间里,OD矩阵估计技术在很长一段时间内承担了在已知部分路段流量观测值条件下去推断整体OD的重任,且从已知约束条件检验的角度来说起到了较好的效果。但由于长期以来受制于数据条件障碍,真实OD矩阵仍很难获取,即便是当前的数据获取和挖掘技术条件下依然有较大的难度,缺少一个评估OD矩阵估计方法有效性的完备方法和绝对真值矩阵支持。本文尝试运用模拟仿真的方法提供一种对比检验方法,对OD估计结果进行检验,有助于比较不同的估计输入所得到结果的相对合理性和可靠性。随着城市治理的精细化和数字化深入发展,城市交通治理也迫切需要高精度、可用的交通模型量化分析提供支撑,结合数据资源能力的提升,对交通模型分析方法的有效性和可靠性进行检验,有助于提升量化分析的可信度。
文章结果显示,初始矩阵的质量对OD估计结果有着决定性影响。特别是对大型网络交通模型而言,运用构造法建立的初始矩阵作为估计过程的初始输入,其得到的估计矩阵即便观测值检验能够符合相关的要求,但与真实OD矩阵之间依然存在着严重偏差,在大部分情况下几乎可以认为是该方法是无效的。小型网络交通模型测试结果显示,OD估计方法能够逐渐逼近真实OD矩阵,特别是在考虑交叉口转向流量的强约束条件下,在检验指标误差方面可以做到十分微小,但从贴近真实矩阵分布角度要求,初始矩阵质量仍然是决定性的变量。当前,随着大规模时空位置数据和交通运行监测数据的普及,为获得和逼近真实出行OD矩阵创造了条件,有可能获得较高质量的初始矩阵,这也为OD估计技术适用于大型交通模型创造了条件。总之,OD估计技术方法有用但存在一定局限性,理解问题的成因更加有助于正确、恰当的开展运用。
本文章发表于《交通工程》杂志第23卷 第6期,徐同学公众号经作者授权发布。
文章作者:陈先龙1,张华2,马毅林3,宋程1
(1.广州市交通规划研究院有限公司,广东 广州 510030;2.同济大学磁浮交通工程技术研究中心 上海 201804;3.北京交通发展研究院 北京 100073)
参考文献
[1] de DIOS ORTÚZAR J, WILLUMSEN L G. Modelling Transport[M]. 4th. Chichester: John Wiley & Sons, Ltd, 2010.
[2] Van ZUYLEN H J, WILLUMSEN L G. The most likely trip matrix estimated from traffic counts[J]. Transportation Research Part B: Methodological, 1980,14B(3): 281-293.
[3] SPIESS H. A Gradient Approach for the O-D Matrix Adjustment problem[R]. Montreal: Universite de Montreal, 1990.
[4] SPIESS H. A maximum-likelihood model for estimating origin-destination matrices[J]. Transportation Research Part B: Methodological, 1987,21B(5): 395-412.
[5] NIELSEN O. Two New Methods for Estimating Trip Matrices from Traffic Counts[M]//Travel behaviour research : updating the state of play. Kidlington: Elsevier Science, 1998:221-250.
[6] CITILABS. CUBE ANALYST reference guide[R]. Lafayette: Citilabs, 2013.
[7] Design manual for roads and bridges[R]. London: THE HIGHWAYS AGENCY, 1997.
[8] 陈先龙. 中国城市交通模型现状问题探讨[J]. 城市交通, 2016,14(02): 17-21.
[9] WILLUMSEN L. Estimation of an 0-D matrix from traffic counts - a review[R]. Leeds: University of Leeds, 1978.
[10] LOW D E. A New Approach to Transportation Systems Modelling[J]. Traffic Quarterly, 1972,26(3): 391-404.







 =0.99
=0.99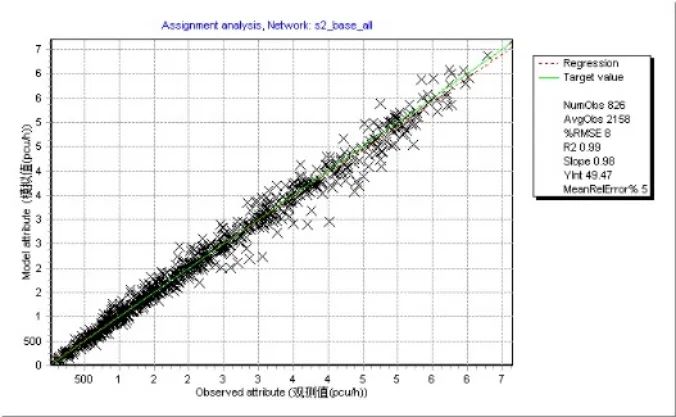
 =0.99
=0.99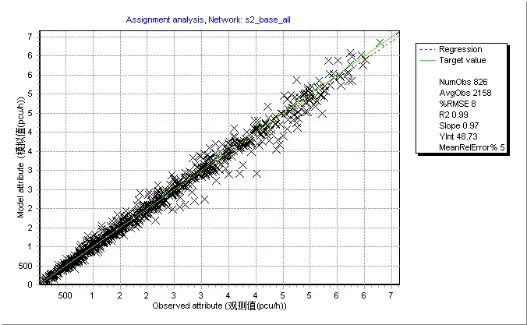
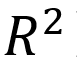 =0.99
=0.99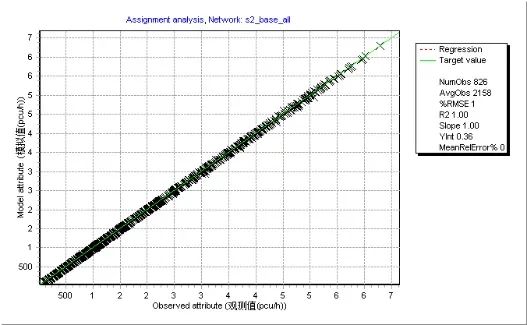
 =1.0
=1.0
 =1.0
=1.0





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








