一、什么是Diffusion
1.前向公式介绍

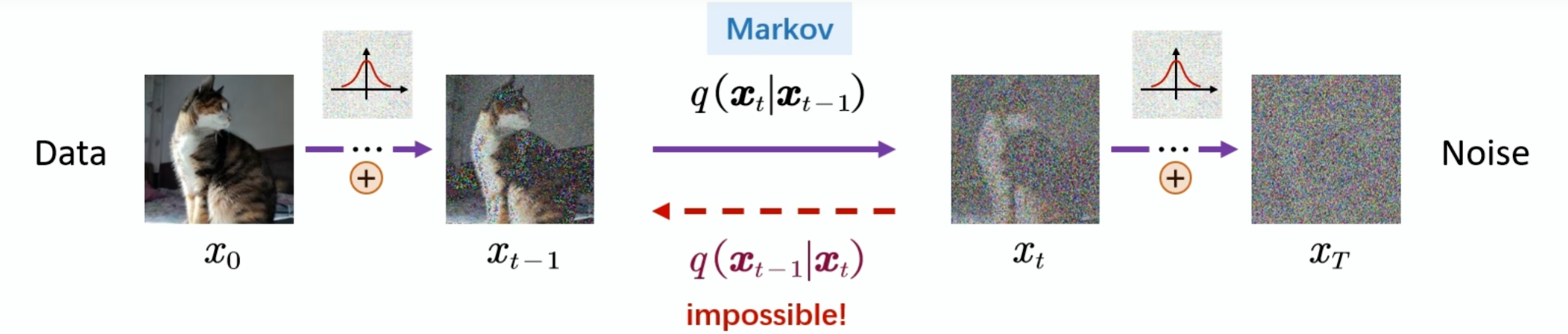
首先定义一个前向过程,给定一张原始图片,通过t次加入噪音,得到一张杂乱无章的照片,那么是否有一个反向的过程,从噪声中恢复出原图:

比如在t-1步我们加入一个分布为高斯分布的噪声:
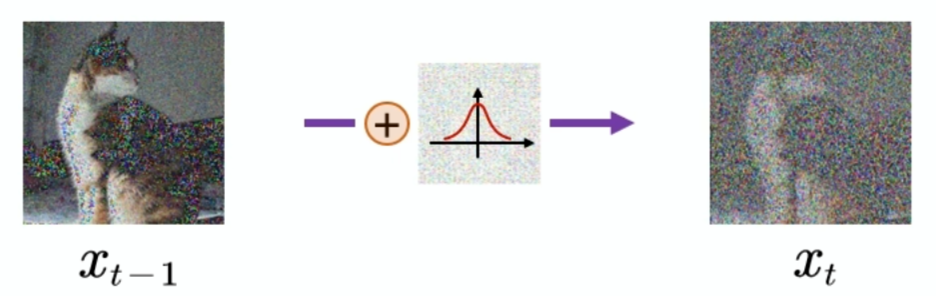
对于反向过程来说,就是训练一个神经网络,可以预测一个噪声,但后把Xt减去预测的噪声就得到Xt-1,我们把这个过程称为去噪的过程:
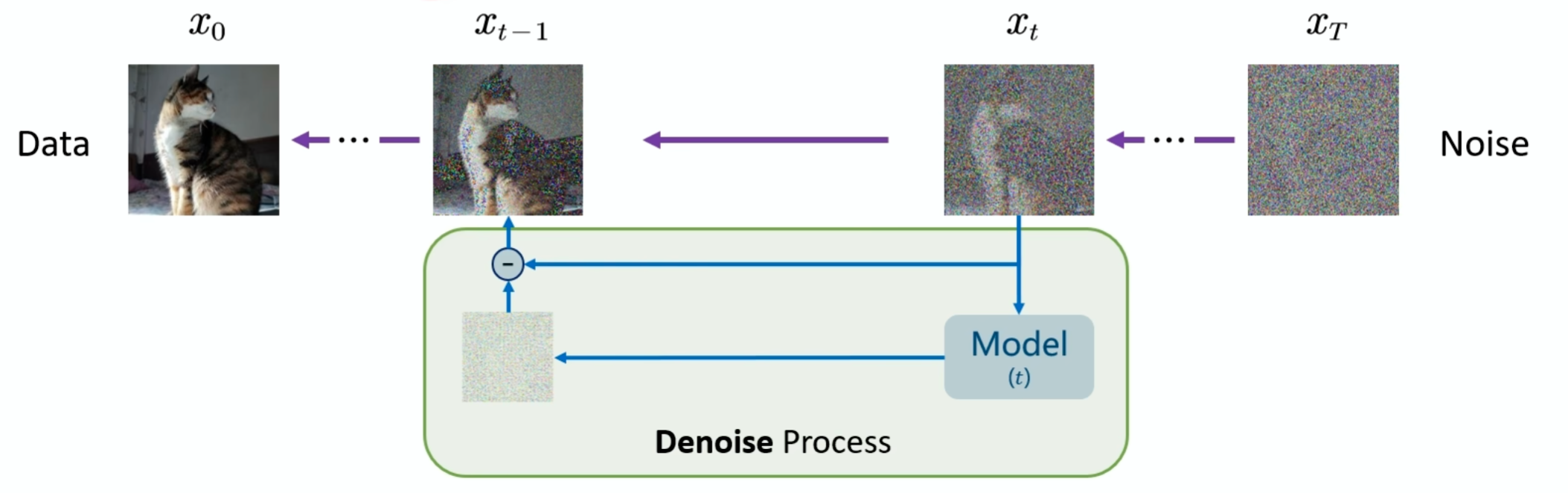
在加入噪声的时候会定义两个系数:
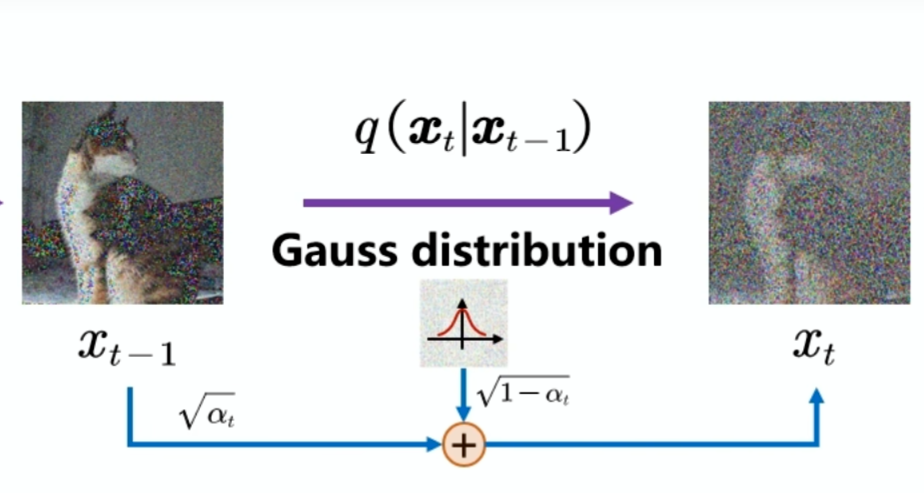
而添加噪声后的图像会满足高斯分布,核心公式就是:
![]()
前半部分表示保留上一部分的数据信息,后半部分表示加入的随机噪声,此时条件分布服从高斯分布此时Xt-1不再是 “随机变量”,而是一个确定的常数。结合正向扩散公式,由于 “常数+ 高斯随机变量” 的结果仍为高斯随机变量,因此无论Xt-1本身是否服从高斯分布,只要固定 (Xt-1,Xt) 的条件分布就一定是高斯分布。
当我们把公式展开:

就得到最后这么一个式子,所以之前的加噪过程就可以变成下图所示的跳跃式加噪:
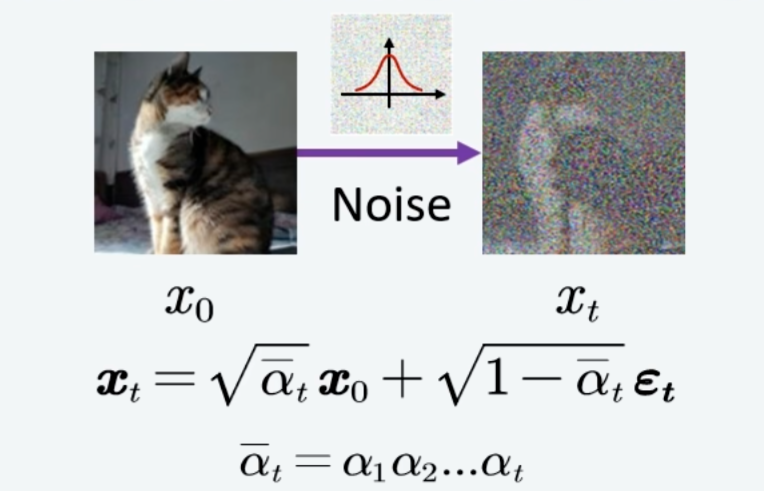
整个过程遵循马尔可夫链。
2.反向公式介绍
在扩散模型的反向扩散过程中,核心目标是从第 t 步的带噪声数据Xt出发,逐步恢复出第 t-1步的带噪声数据 Xt-1,最终迭代到原始数据 X0。
正向过程中我们有前面的公式,但是在反向过程中由于我们不知道Xt-1和原始噪声,我们需要训练一个模型比如Unet预测出原始噪声,从而通过正向公式的逆运算,推导出原始数据。
最大似然估计
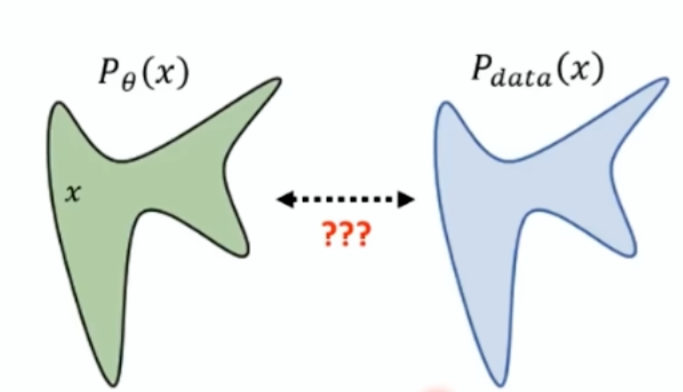
我们要使用神经网络去拟合一个我们观察到的数据的分布,我们希望能找到一个参数,使我们生成的图像的真实概率是比较高的,对应的就是求一个最大似然估计,那我们要求这个的话就等价于求一个最小的下面这个值:
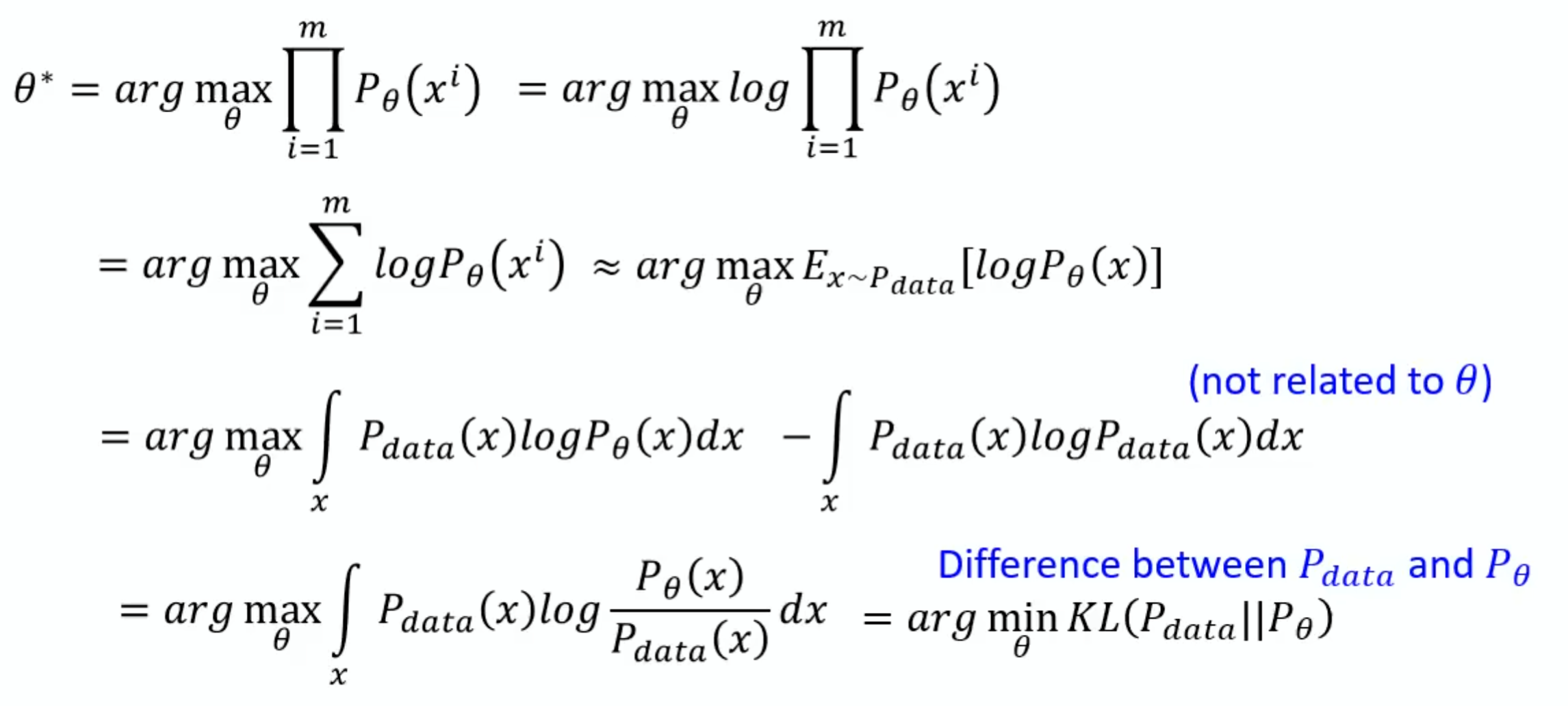
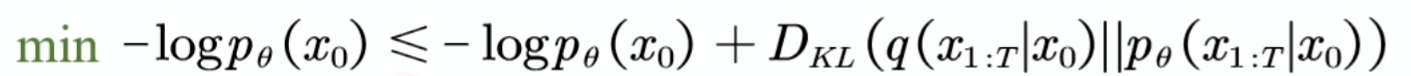
后面的代表KL散度,通过推导我们可以得到下面的这个东西:ELBO
二、数学原理
先看Training部分:第二行意思就是我们先要sample一张图片也就是X0,通常把X0当作干净的图,第三行就是从1到T之间sample一个数字出来,第四行就是sample一个噪音,大小和图像一样,然后第五行就是比较复杂的:在本文的一部分的前向公式中提到的,先看括号里,前面的式子,是对X0和噪音做加权求和,前面的参数就是事先定好的weight;右边这个就是Noise predictor network,目的就是得到左边的那个
就是Target Noise也就是当初sample出来的Noise,这就是这个算法真正做的东西。

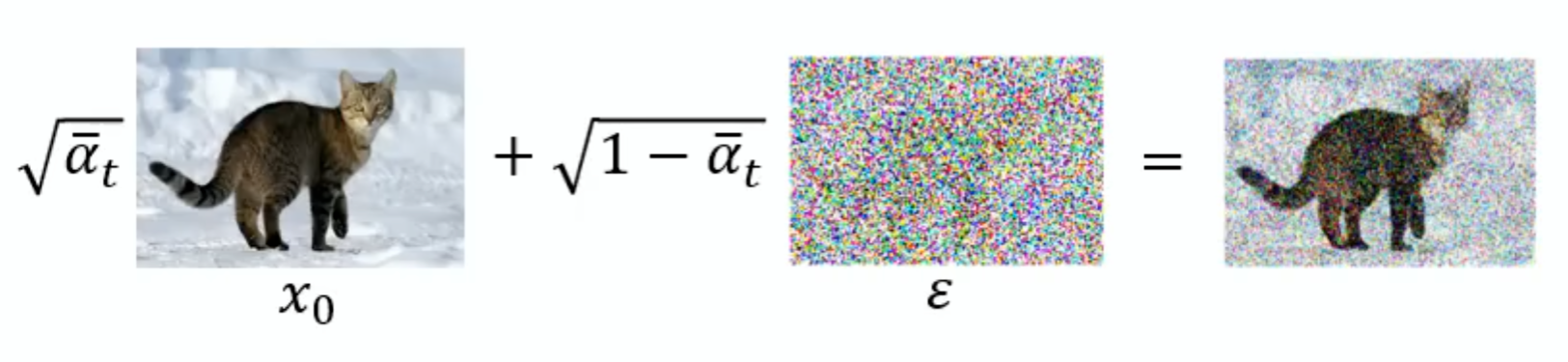
接下来是产生图的过程:
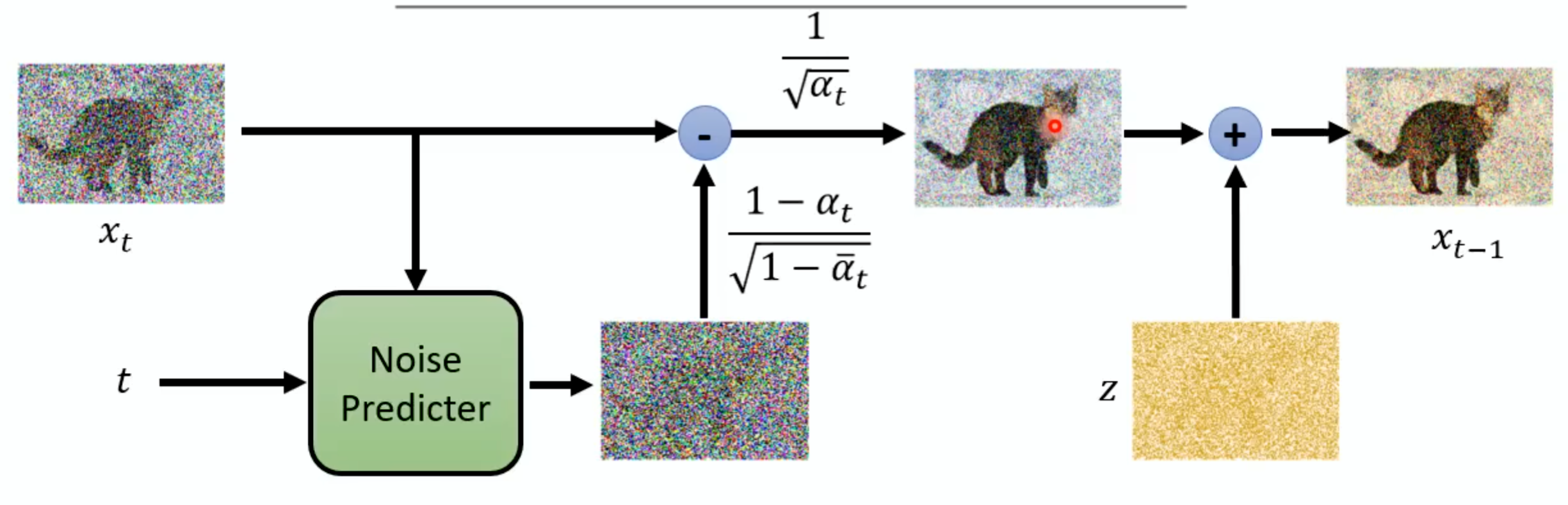
一开始sample一个全部都是noise的图,叫为,接下来跑T次操作:第三行是sample一个noise放到第四行的公式后面,目的是为了增加干扰,第四行中的
就是上一个步骤产生的图,在最开始的时候就是
。


整个过程图示如下:




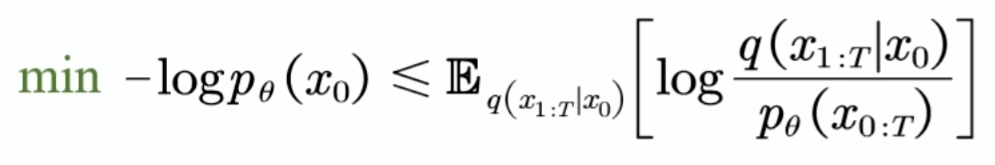

















 1817
1817

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










