java递归简单递归

原创于 2021-11-11 23:25:52 发布 · 741 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#java #递归法 #递归算法

这篇博客深入浅出地讲解了递归的概念，并通过实例——走阶梯问题，详细阐述了递归的应用。文章指出在解决阶梯问题时，递归公式为f(n)=f(n-1)+f(n-3)，并明确了错误的终止条件。接着，作者给出了递归求解阶梯走法的具体步骤，以及不同台阶数的走法数量。最后，文章还提及了使用递归进行乘法运算的定义。

详细的讲解一下递归

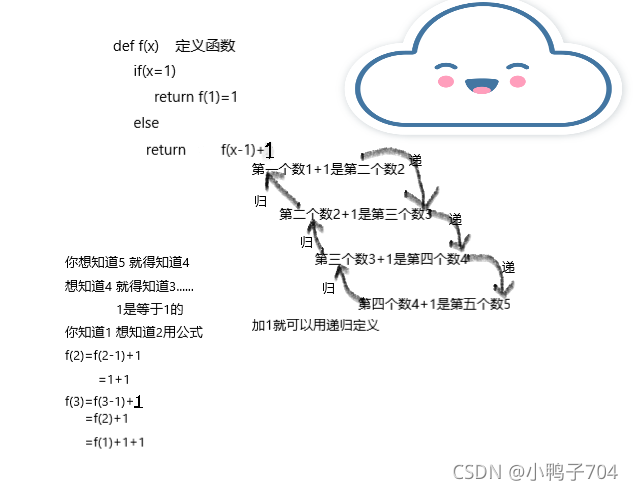
用一个走阶梯的例子每一次走一步或者三步

f(n)=f(n-1)+f(n-3) 当f(1)=f(1-1)+f(n-3) 第一个等于0 错误

当f(2)=f(2-1)+f(2-3) 第一个二负数错误

当f(3)=f(3-1)+f(3-3) 第二个等于0 错误这些就是终止条件

f(1)=1 f(2)=1 f(3)=2

第一个台阶有一种走法第二个台阶有一种走法第三个台阶有两个走法

第四个台阶有三种走法一步三步一步一步一步三步一步

public class DiGui_TaiJie {
    public static void main(String[] args) {
        for (int i = 1; i < 6; i++) {
            System.out.println(i+"个台阶"+f(i)+"种算法");
        }
    }
    public static int f(int n){
        if (n==1)return 1;
        if (n==2)return 1;
        if (n==3)return 2;
        return f(n-1)+f(n-3);
    }
}

定义一个乘法递归

public long factorial( long number )
    {                  
        if ( number <= 1 )  
            return 1;
        else
            return number * factorial(number- 1 );
    } 
 //   例如number是5    
 //           return  5*       factorial(4) 
 //                   5*4*     factorial(3) 
 //                   5*4*3*   factorial(1) 
 //                   5*4*3*2* factorial(1)
 //                   5*4*3*2*1