[OJ]数据结构：链表回文

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};
*/

typedef struct ListNode Node;

class PalindromeList {
public:
    bool chkPalindrome(ListNode* A) {
        // 空链表或单个节点链表都是回文
        if (A == NULL || A->next == NULL) 
        {
            return true;
        }
        
        //使用快慢指针找到链表中点
        Node* fast = A;
        Node* slow = A;
        Node* prev = NULL;
        
        // 快指针每次走两步，慢指针每次走一步
        // 当快指针到达链表末尾时，慢指针正好到达中点（或中点前一个）
        while (fast != NULL && fast->next != NULL) 
        {
            prev = slow;  // 记录慢指针的前一个节点
            fast = fast->next->next;
            slow = slow->next;
        }
        
        // 将链表从中间断开，分为前后两部分
        // 注意：prev可能是NULL（当链表只有两个节点时）
        if (prev != NULL) 
        {
            prev->next = NULL;
        }
        
        // 反转后半部分链表
        Node* l1 = NULL;     // 反转后新链表的头节点
        Node* l2 = slow;     // 当前待反转的节点
        Node* l3 = NULL;     // 临时保存下一个节点
        
        while (l2 != NULL) 
        {
            l3 = l2->next;   // 保存下一个节点
            l2->next = l1;   // 当前节点指向前一个节点
            l1 = l2;         // 更新新链表的头节点
            l2 = l3;         // 移动到下一个待反转节点
        }
        
        // 此时l1是反转后的后半部分链表的头节点
        slow = l1;
        
        // 比较前后两部分链表
        Node* front = A;
        
        while (front != NULL && slow  != NULL) 
        {
            if (front->val != slow ->val) 
            {
                return false;  // 发现不匹配，不是回文
            }
            front = front->next;
            slow = slow ->next;
        }
        
        // 注意：链表长度可能是奇数，此时后半部分会比前半部分多一个节点
        // 但这个多出来的节点是原链表的中间节点，不需要比较
        
        return true;  // 所有节点都匹配，是回文
    }
};

三、图解

假设有链表A：

1.初始化

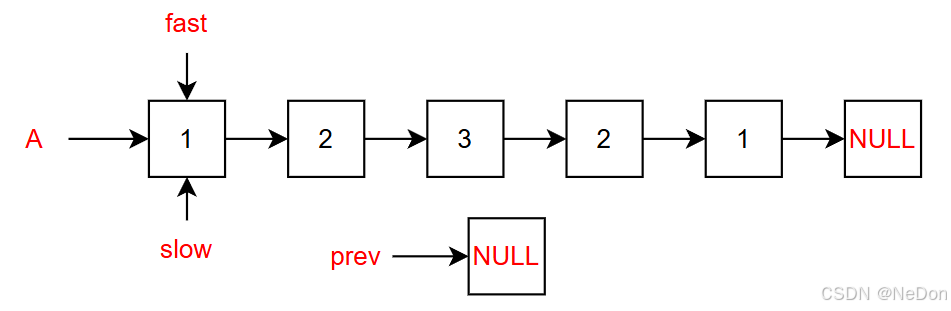
2.获取中间节点

fast指针每次向后走两步，slow指针每次往后走一步，当fast指针到达最后一个节点或者NULL到达NULL时，slow正好落于链表的中间节点，prev指针指向前链表的末端。

fast = NULL || fast->next = NULL；

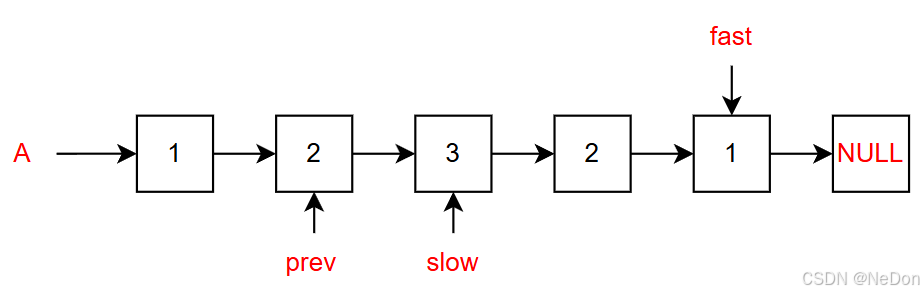
此时：
prev = 节点2，正好是前链表的最后一个节点，需要将其next指向NULL；
slow作为后一个链表反转的初始头（后面将是尾）；

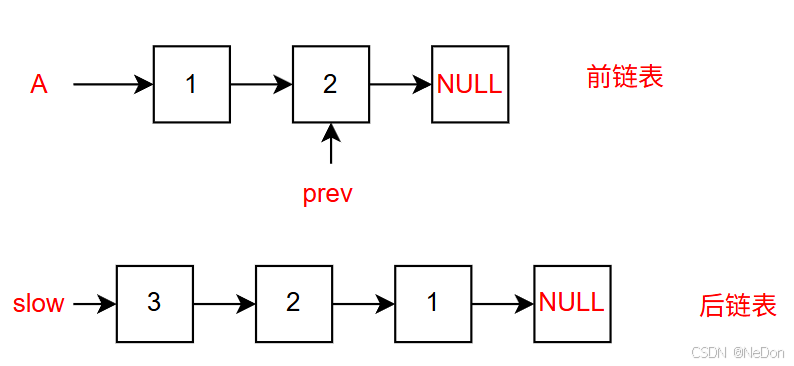
3.反转后链表

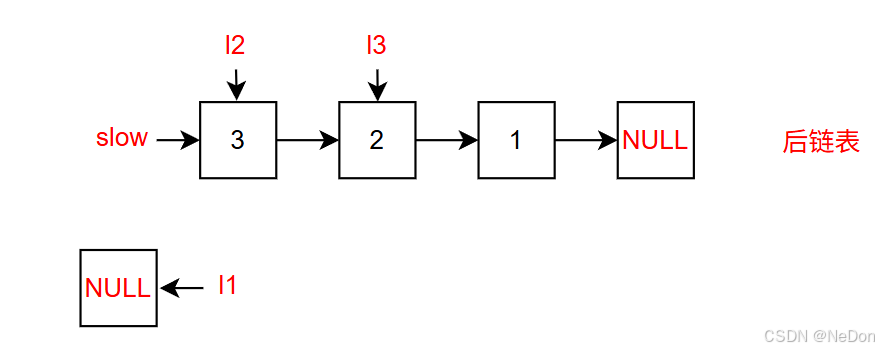
参考反转链表的实现，我们可以得到以下新链表

至此，我们已经获取了两个链表，分别为前链表和后链表

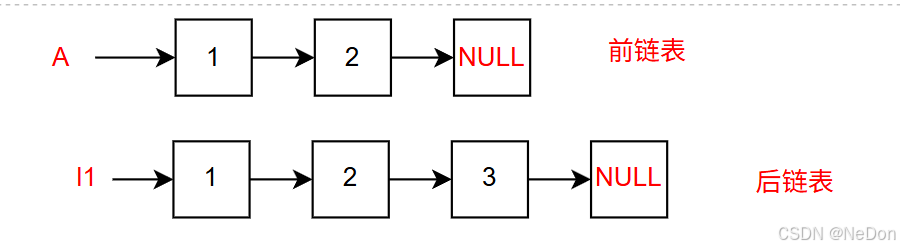
4.比较链表

这里为了避免更改原链表头指针，我们可以将slow指针重新指向后一个链表的头节点，然后创建一个指针指向前链表的头节点。

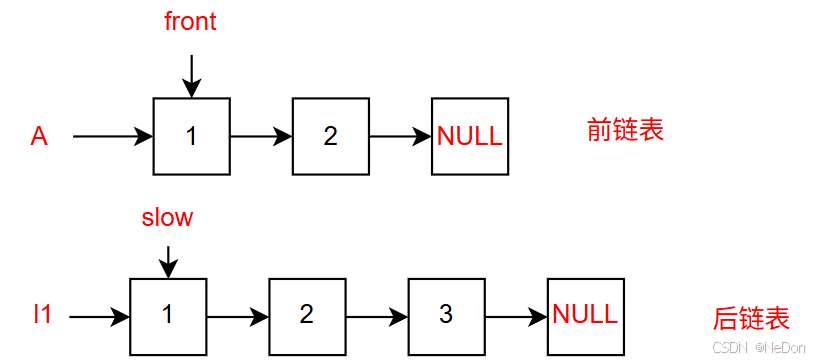
比较过程：
1. front=1, back=1 → 相等
2. front=2, back=2 → 相等
3. front=NULL, back=3 → 前半部分结束

虽然后半部分还有节点3，但这是原链表的中间节点，不需要比较，所以链表是回文结构

四、常见错误与注意事项

1.边界处理

// 错误：没有处理空链表或单节点链表
// 正确做法：
if (A == NULL || A->next == NULL) 
{
    return true;
}

2.快慢指针终止条件

// 错误：只检查fast->next，可能访问空指针
while (fast->next) // 如果fast为NULL，会访问空指针的next
{  
    fast = fast->next->next;
    slow = slow->next;
}

// 正确：同时检查fast和fast->next
while (fast != NULL && fast->next != NULL) 
{
    fast = fast->next->next;
    slow = slow->next;
}

3.链表断开时空指针问题

// 错误：假设prev总是非空
prev->next = NULL;  // 如果链表只有两个节点，prev可能是NULL

// 正确：检查prev是否为空
if (prev != NULL) 
{
    prev->next = NULL;
}

4.比较的终止信号

// 错误：只比较到其中一个链表结束
while (front != NULL) // 如果后半部分比前半部分短，会访问空指针
{  
    if (front->val != slow->val) 
    {
        return false;
    }
    front = front->next;
    slow= slow->next;
}

// 正确：两个链表都要检查
while (front != NULL && slow!= NULL) 
{
    if (front->val != slow->val) 
    {
        return false;
    }
    front = front->next;
    slow= slow->next;
}