PTA畅通工程之最低成本建设问题(用并查集实现Kruskal算法)

原创已于 2024-08-29 16:46:59 修改 · 505 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #数据结构

于 2022-04-03 11:25:58 首次发布

ACM 专栏收录该内容

36 篇文章

订阅专栏

本文探讨了如何利用Kruskal算法求解实际生活中的城镇交通‘畅通工程’问题，通过计算候选道路的改建成本，找到最低成本路径以实现区域间的快速交通连接。

某地区经过对城镇交通状况的调查，得到现有城镇间快速道路的统计数据，并提出“畅通工程”的目标：使整个地区任何两个城镇间都可以实现快速交通（但不一定有直接的快速道路相连，只要互相间接通过快速路可达即可）。现得到城镇道路统计表，表中列出了有可能建设成快速路的若干条道路的成本，求畅通工程需要的最低成本。

输入格式:

输入的第一行给出城镇数目N (1<N≤1000)和候选道路数目M≤3N；随后的M行，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号（从1编号到N）以及该道路改建的预算成本。

输出格式:

输出畅通工程需要的最低成本。如果输入数据不足以保证畅通，则输出“Impossible”。

输入样例1:

输出样例1:

输入样例2:

输出样例2:

Impossible

该题是典型的求最小生成树问题。

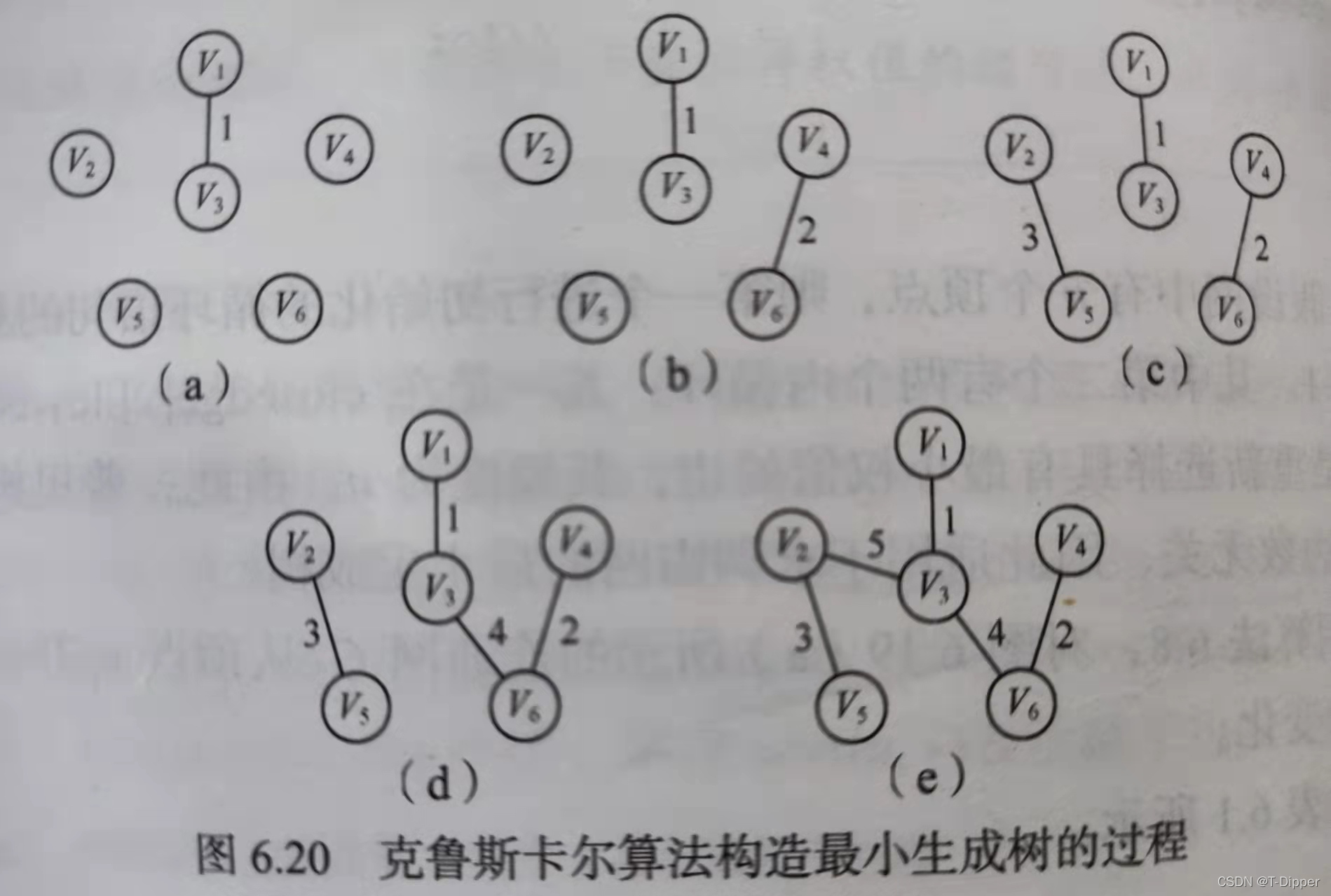
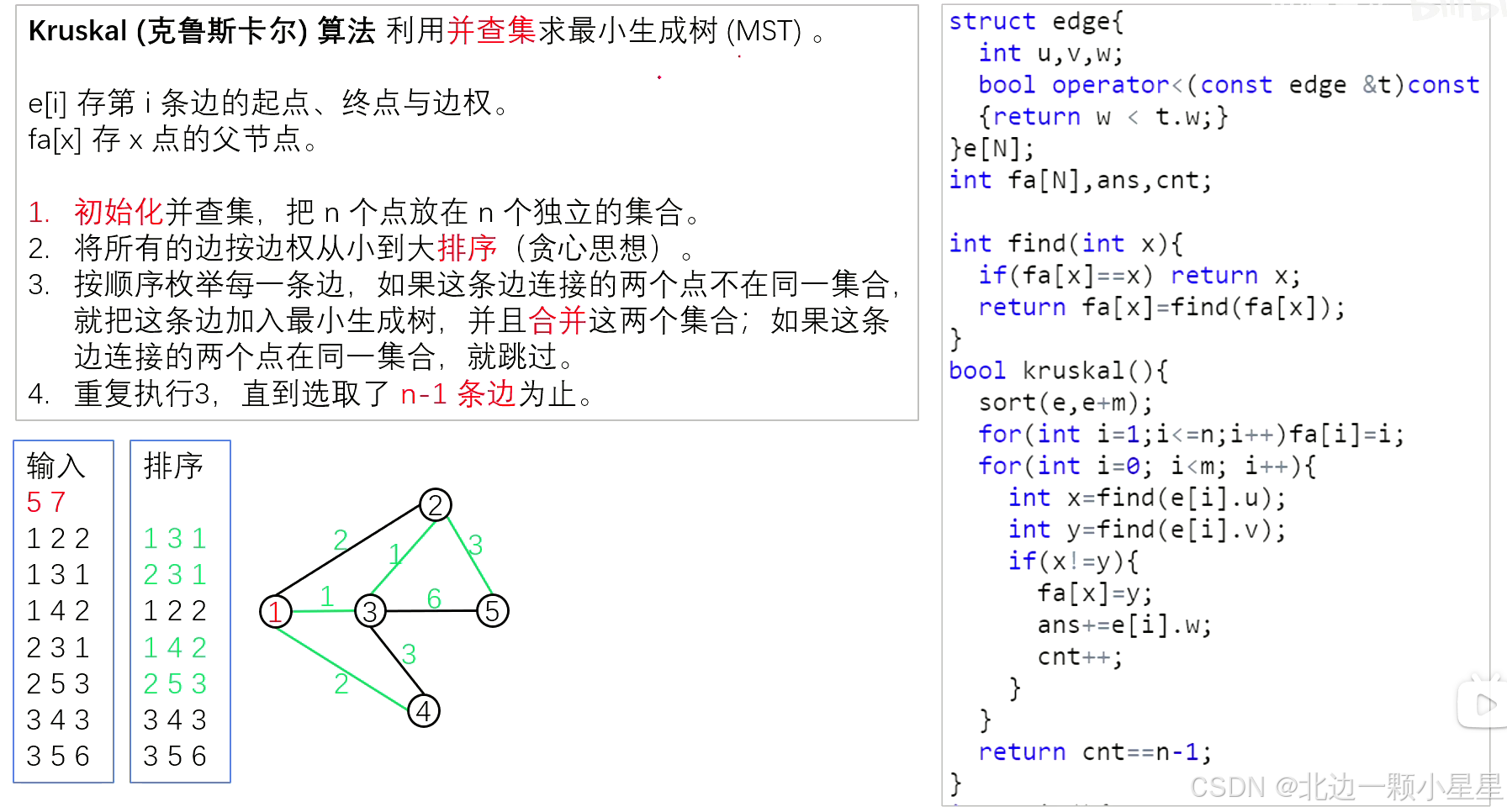
下面简述下求最小生成树中的Kruskal算法：

先去掉所有边，然后每次选择一条权值最小且不构成回路的边，直到所有顶点都并入。

本题AC代码：

#include<bits/stdc++.h> 
using namespace std;
int n,m;
int fa[1001];
struct node
{
	int x,y,w;
}a[3001];
bool cmp(node a,node b)
{
	return a.w<b.w;
}
int find(int x)
{
	return x==fa[x]?x:fa[x]=find(fa[x]);
}
int kru()
{
	int cnt=n;
	int sum=0;
	for(int i=0;i<m&&cnt>1;i++)
	{
		int x=find(a[i].x);
		int y=find(a[i].y);
		if(x!=y)
		{
			fa[x]=y;
			sum+=a[i].w;
			cnt--; 
		}
	}
	if(cnt>1) return -1;
	else return sum;
}
int main()
{
	cin>>n>>m;
	for(int i=0;i<m;i++)
	cin>>a[i].x>>a[i].y>>a[i].w;
	sort(a,a+m,cmp);
	for(int i=1;i<=n;i++)
	fa[i]=i;
	int res=kru();
	if(res==-1) cout<<"Impossible";
	else cout<<res;
	return 0;
}

如果对并查集不太熟悉或者对基本操作淡忘了可以先移步到此看看并查集的典型题目及操作模板：(1条消息) PTA朋友圈（并查集的应用）_T-Dipper的博客-CSDN博客https://blog.csdn.net/weixin_61725823/article/details/123607919