边那些一个递归算法,在一棵有n个几点的、随机建立起来的二叉排序树上查找第k(1<=k<=n)小的元素并返回指向该节点的指针。要求算法的平均时间复杂度为O(log2n).二叉排序树的每个结点中除data,lchild,rchild等数据成员外,增加一个count成员,保存以该节点为根的子树上的结点个数
#include <iostream>
#include <queue>
typedef struct node{
int data;
struct node* left;
struct node* right;
int count;
}node,*pnode;
pnode buynode(int x)
{
pnode tmp=(pnode) malloc(sizeof (node));
tmp->data=x;
tmp->left= nullptr,tmp->right= nullptr,tmp->count=0;
return tmp;
}
void build_tree(pnode &root,int data)
{
if(root== nullptr) {
root= buynode(data);
return;
}
if(data<root->data)build_tree(root->left,data);
if(data==root->data) return;
if(data>root->data) build_tree(root->right,data);
}
void print(pnode root)
{
if(root== nullptr) return;
std::queue<pnode> record;
record.push(root);
int size=record.size();
while(!record.empty()){
pnode head=record.front();
printf("%3d",head->data);
record.pop();
if(head->left) record.push(head->left);
if(head->right) record.push(head->right);
if(--size==0) puts(""),size=record.size();
}
}
void set_count(pnode &root)
{
if(root== nullptr) return;
int count = 1; // 初始化节点计数为1,包括当前节点
if(root->left) {
set_count(root->left);
count += root->left->count;
}
if(root->right) {
set_count(root->right);
count += root->right->count;
}
root->count = count;
}
pnode search_small(pnode root,int k)
{
if(k<1||k> root->count) return nullptr;
if(root->left== nullptr)
{
//如果没有左子树,并且k==1,那么第一小的结点就是当前根节点
if(k==1) return root;
//因为没有左子树,并且当前结点比它的右节点的全部节点都要小,所以在右子树中找第k-1小的结点
if(root->right&&k>1) return search_small(root->right,k-1);
}else{
if(root->left->count==k-1) return root;
//左子树的结点个数比k-1多,继续从左子树中找第k大的结点
if(root->left->count>k-1) return search_small(root->left,k);
//如果左子树的节点小于k个,并且算上当前的节点也没有k个,那么要查找的结点就在右子树里面
//当前结点和左子树的值都是要比当前结点的右子树的值要小的,所以要在右子树查找k-左子树节点数-当前节点本身(1)
if(root->left->count<k-1) return search_small(root->right,k-root->left->count-1);
}
}
int main() {
pnode r1= nullptr;
//p295图7.8(a),这是一棵平衡二叉排序树
int a[]={45,24,12,37,28,40,55,53,60,70};
for(int i=0;i<10;i++)
{
build_tree(r1,a[i]);
}
print(r1);
set_count(r1);//将每个结点的count值设置好
puts("");
for(int i=0;i<10;i++)
{
printf("the node number %3d is the %3d th small number \n", search_small(r1,i+1)->data,i+1);
}
return 0;
}
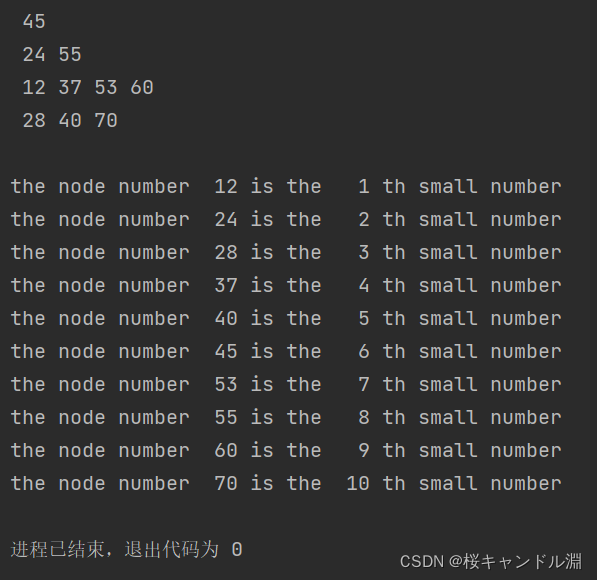





 文章描述了一种在随机建立的二叉排序树中,通过递归算法查找第k小元素的解决方案,利用节点的count属性优化平均时间复杂度为O(log2n),并给出了一个实际操作的例子。
文章描述了一种在随机建立的二叉排序树中,通过递归算法查找第k小元素的解决方案,利用节点的count属性优化平均时间复杂度为O(log2n),并给出了一个实际操作的例子。

















 434
434

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










