代码随想录D15: 二叉树 Python Part03-CSDN博客

222. 完全二叉树的节点个数

要点：

使用层序遍历，直接返回节点总数是一种相对直观的解法，利用层序模板稍加改动即可

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        
        if not root:
            return 0
        
        queue = collections.deque([root])
        results = []

        while queue:
            level = []
            for _ in range(len(queue)):
                node = queue.popleft()
                level.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            
            results.extend(level)
        
        print(results)
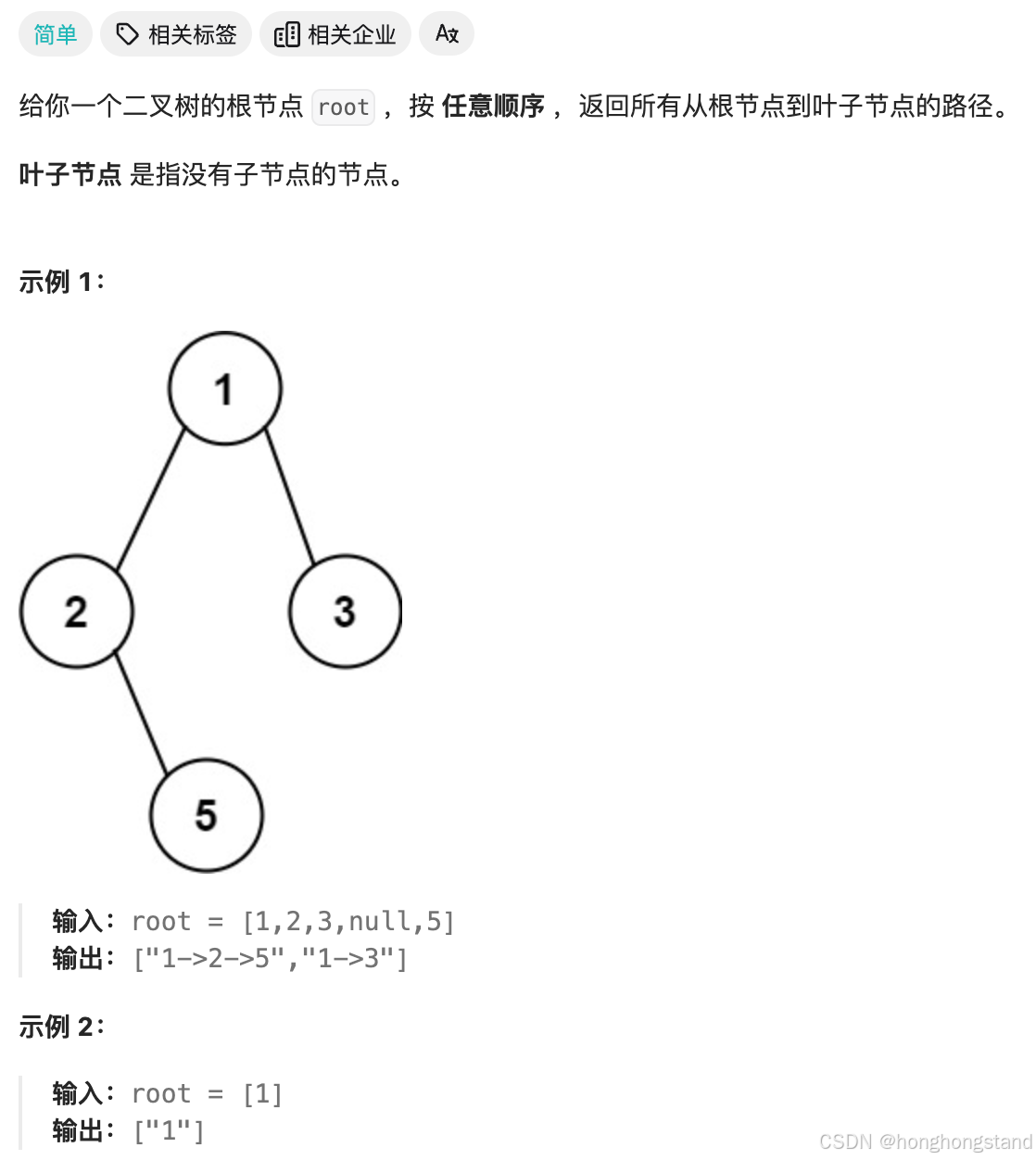
        return len(results)

257. 二叉树的所有路径

要点：

本题需要记录路径，因此应该使用前序遍历。使用前序遍历会先记录节点，然后再遍历左右节点。

这道题目涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    ## 输出节点，单条路径，最终结果
    def traversal(self, cur_node, path, result):

        path.append(cur_node.val) # 将节点数值先放入路径
        # 使用result存放单条路径的结果
        if not cur_node.left and not cur_node.right:
            result.append('->'.join(map(str, path)))
            return
        
        if cur_node.left:
            self.traversal(cur_node.left, path, result)
            # path 记录的是从根节点到叶子结点的路径
            # 将path弹出元素表示在回溯过程中从path挨个去除当前路径节点信息
            path.pop()
        
        if cur_node.right:
            self.traversal(cur_node.right, path, result)
            path.pop()
        

    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        result, path = list(), list()
        if not root:
            return []
        
        self.traversal(root, path, result)

        return result

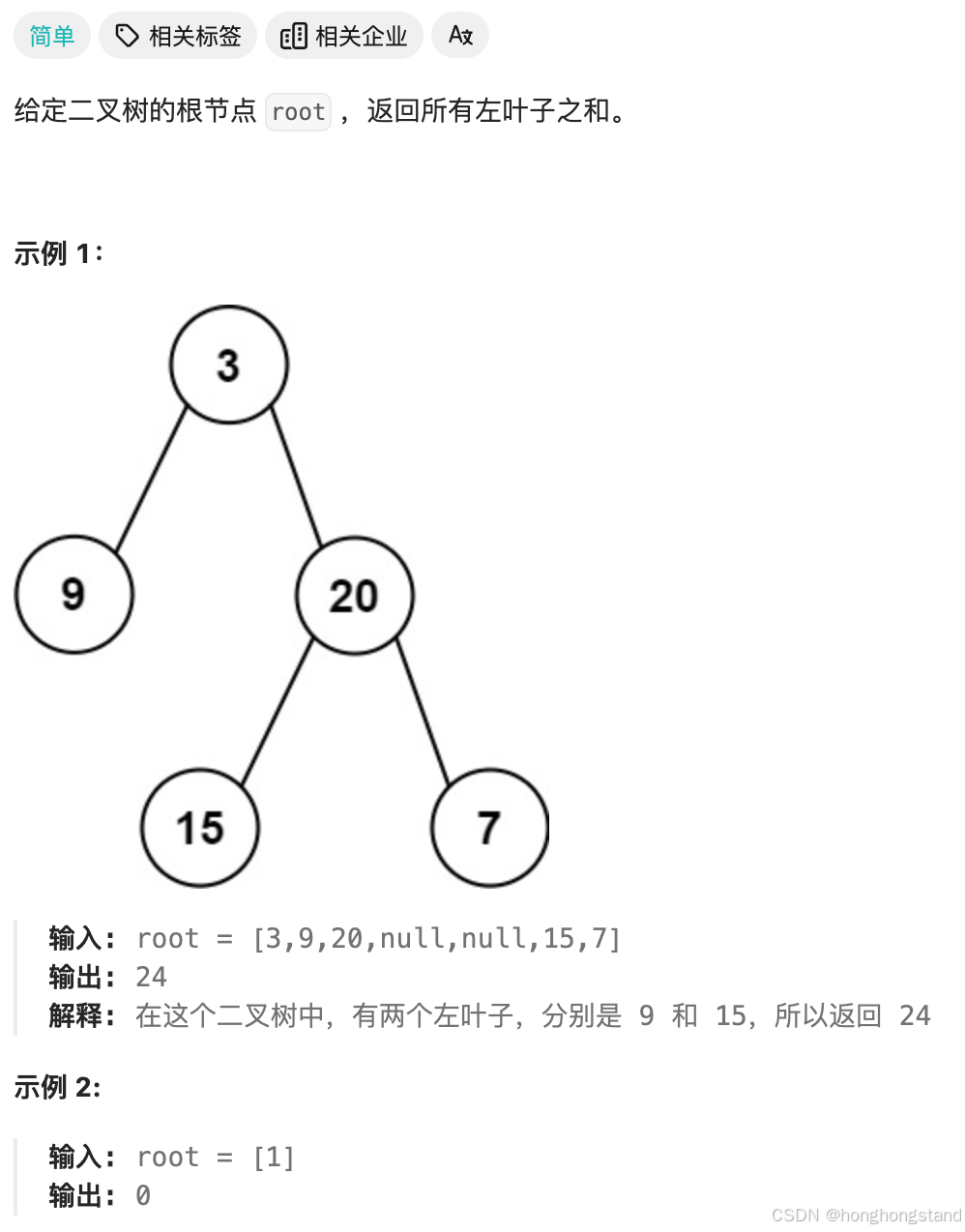
404. 左叶子之和

要点：

左叶子节点的定义是指，该节点是叶子节点，同时不是其父节点的右孩子节点。

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.ans = 0

    def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:

        if root is None:
            return 

        if root.left and root.left.left is None and root.left.right is None:
            self.ans+=root.left.val
        
        self.sumOfLeftLeaves(root.left)
        self.sumOfLeftLeaves(root.right)

        return self.ans

110. 平衡二叉树

要点：

采取后序遍历，左右中进行统计。判断左子树高度，右子树高度，比较左右子树高度差。

明确参数：当前传入节点。返回值：以当前传入节点为根节点的树的高度。

如果在遍历过程中，检测到左右节点相差高度已经达到了1以上，那么直接返回负值进行标记；如果以目前节点为根节点的的二叉树都是平衡二叉树（左右子树高度差不大于1），那么继续向下探索。

终止条件：node为空节点时，递归终止。

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        
        if self.get_height(root) == -1:
            return False
        else:
            return True
    
    def get_height(self, node):

        # 空节点则返回 0
        if not node:
            return 0
        
        # 使用海象运算符，先给left_h赋值，如果值为-1，则直接返回-1
        if (left_h := self.get_height(node.left)) == -1:
            return -1
        
        if (right_h := self.get_height(node.right)) == -1:
            return -1

        # 左右节点深度相差超过1则判负
        if abs(right_h - left_h) > 1:
            return -1
        else:
            # 需要记清楚高度，隐式传递，这样才能在回溯时比较高度
            return 1 + max(right_h, left_h)