代码随想录D16: 二叉树 Python Part04

513. 找树左下角的值

要点：

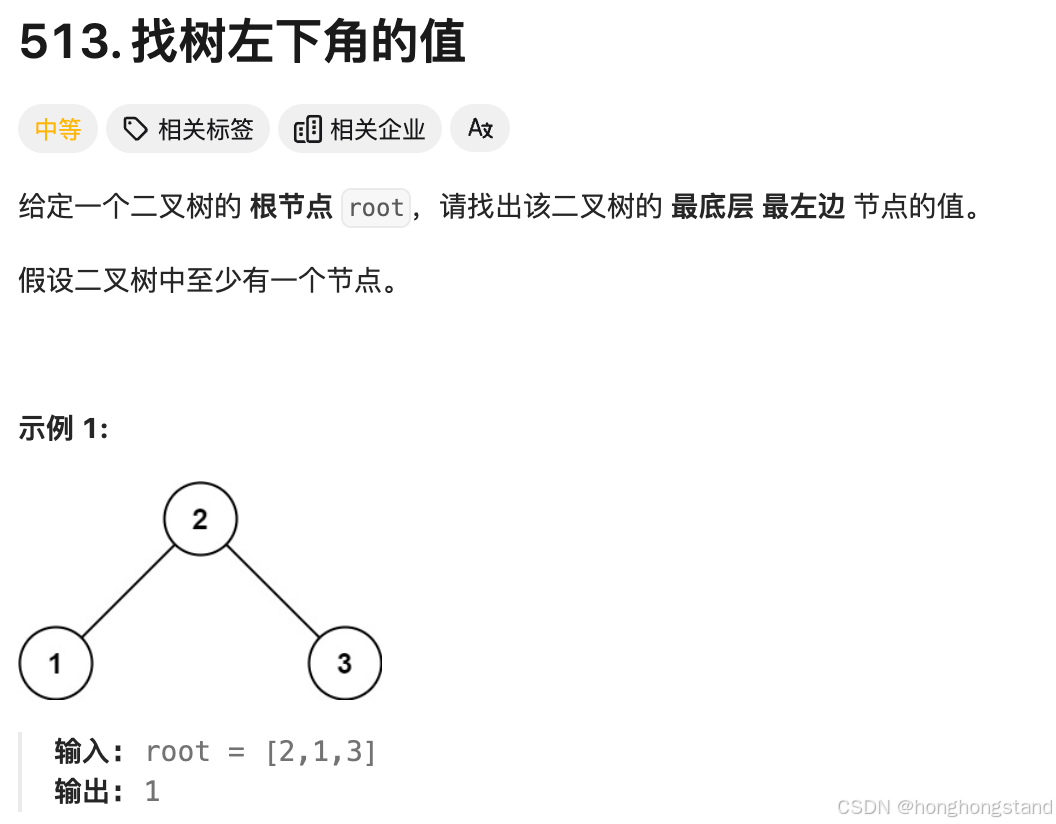
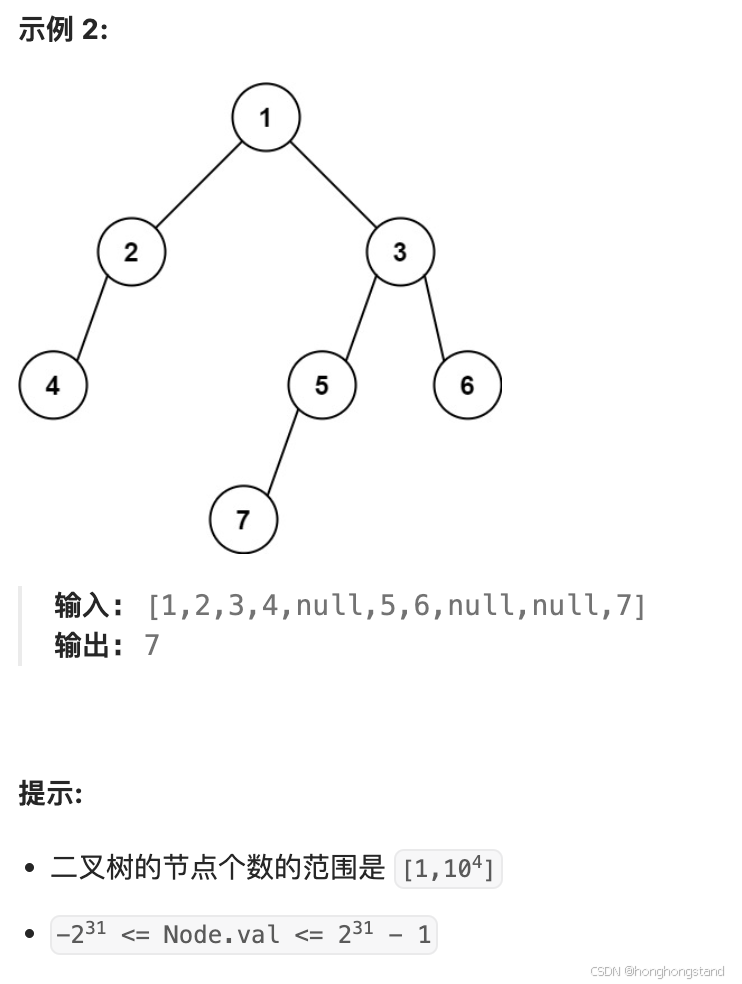
从题意中可以看到，向左遍历到最后一个，此时的节点未必是最后一行的节点，这是本题的难点。

所以本题的题意应当是：在树的最后一行找到最左边的值。首先要是最后一行，然后是最左边的值。

因此，首先我们可以找出深度最大的叶子结点；在递归过程中优先搜索左侧节点，最后即可获得左下角的值。

解法：

前序，中序，后续遍历都可以，只要注意先遍历左侧子节点即可

0. 全局变量：定义一个最大深度，result记录左下角的值

1. 确定输入和输出：输入节点和当前深度，不需要返回值

2. 终止条件：遇到叶子结点即终止，更新最大深度

3. 单步逻辑：

- 首先排除叶子节点，当节点为叶子节点时，评价当前节点是否在最大深度

- 当节点不是叶子节点时，先将深度+1，左孩子节点存在的情况下，先进入左节点；回溯时需要将深度-1.

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        
        self.max_depth = float('-inf')
        self.result = None
        self.traversal(root, 0)
        
        return self.result

    def traversal(self, node, depth):
        if not node.left and not node.right:
            if depth > self.max_depth:
                self.max_depth = depth
                self.result = node.val
                return 

        if node.left:
            depth += 1
            self.traversal(node.left, depth)
            depth -= 1
        
        if node.right:
            depth += 1
            self.traversal(node.right, depth)
            depth -= 1
        

112. 路径总和

要点：

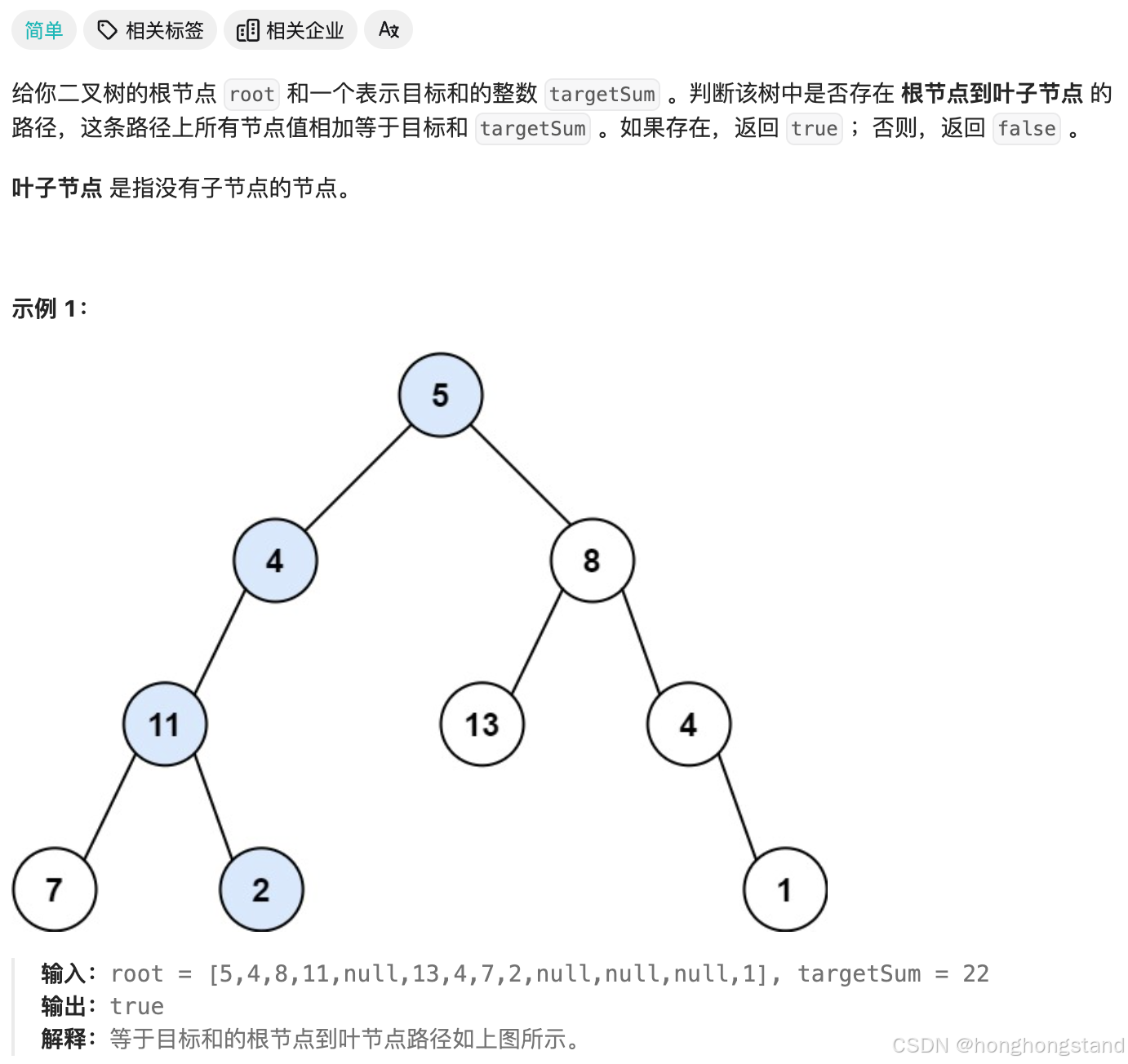
要计算路径总和，就必须记录路径，或者控制路径数值的和，也就涉及到回溯。由于要处理中节点的数值，由于中间节点只有数值获取没有逻辑处理，所以几种遍历顺序都可以使用。

解法：

0. 全局变量：设置路径和

1. 递归函数输入输出：输入节点和当前路径和 返回新的路径和

2. 终止条件：当遍历到叶子节点时，停止遍历并比对路径和和目标值

3. 单层逻辑：首先记录路径和，然后进入一侧的节点，回溯时再减去节点值，任何一条路径符合要求即返回True，否则返回False

实际操作时会发现，需要提前记录下一层节点的信息，这样会便于代码逻辑的构建；同时使用减法逻辑会更简洁。

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        
        return self.traversal(root, targetSum - root.val) if root is not None else False
        
    
    def traversal(self, node, path_sum):
        
        if not node.left and not node.right and path_sum == 0:
            return True
        # 遍历到叶子节点，但总和并不是零
        if not node.left and not node.right:
            return False
            
        if node.left:
            # 使用减法逻辑，每遍历一个节点，减去下一层的值
            # 在叶子节点减到0 说明路径符合要求
            path_sum -= node.left.val
            # 任何一个左侧二叉树符合要求都要及时返回
            if self.traversal(node.left, path_sum):
                return True
            path_sum += node.left.val

        if node.right:
            path_sum -= node.right.val
            if self.traversal(node.right, path_sum):
                return True
            path_sum += node.right.val

        # 左右均没有符合要求的路线
        return False

106. 从中序与后序遍历序列构造二叉树

要点：

中序数组不知道中（根）节点的信息，最左为左叶子，最右为又叶子；后续数组不知道右节点信息，最左为左叶子，最右为根节点。

如何根据两个顺序构造一个唯一的二叉树，就是以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

解法：

第一步：如果数组大小为零的话，说明是空节点了。

第二步：如果不为空，那么取后序数组最后一个元素作为节点元素（根节点）。

第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

第五步：切割后序数组，切成后序左数组和后序右数组

第六步：递归处理左区间和右区间

由于切割数组首先从后序开始，随后会在中序和后续之间来回切换赋值，因此也需要使用递归法来构造整棵树。

以题目案例 in = [9, 3, 15, 20, 7]，post = [9, 15, 7, 20, 3] 为例：

0. 全局变量 无

1. 输入输出：输入 post 和 in ，输出新的经过切割的 post 和 in

2. 终止条件：post 和 in 在经过切分后长度为 1，并经过赋值

3. 单层逻辑：首先取post[-1]，将其作为根节点，使用post[-1]分割 in，根节点的左侧为in分割后的左区间，进入根节点右孩子，使用分割后的in[-1]分割去除了9,3的post。以此类推

实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        
        if not postorder:
            return None

        root_val = postorder[-1]
        root = TreeNode(val = root_val)
        # 设置切割位置
        split_idx = inorder.index(root_val)
        # 中序切割
        inorder_left = inorder[: split_idx]
        inorder_right = inorder[split_idx + 1: ]
        # 注意右侧切分规则，可以先切右区间，参考题例
        postorder_left = postorder[: len(inorder_left)]
        postorder_right = postorder[len(inorder_left): len(postorder) - 1]
        # 注意输入的区间
        root.left = self.buildTree(inorder_left, postorder_left)
        root.right = self.buildTree(inorder_right, postorder_right)

        return root