Python Fraction类实战：生成小学分数四则运算试卷

一、前言

在小学五年级数学中，分数运算占据着至关重要的地位。传统的编程实现方式往往面临两个主要挑战：浮点数精度问题和运算结果标准化问题。当使用浮点数处理分数运算时，像1/3这样的简单分数会被转换为0.333333...的无限循环小数，这种精度丢失在需要精确计算的场景下（如考试系统、教学软件）将造成严重问题。

Python的fractions模块提供的Fraction类完美解决了这一难题。不同于浮点数的近似表示，Fraction类以分子分母的整数对形式精确存储分数值，支持所有基本算术运算并自动执行约分操作。例如

本文将深入解析Fraction类的使用方法，并演示如何结合随机数生成和图像处理技术，构建一个完整的分数四则运算试卷生成系统。

实验所需的库

• fractions 模块：提供了 Fraction 类，用于处理分数及其运算。
• random 模块：用于生成随机整数和随机选择运算符，从而生成各种分数运算题目。
• PIL（Python Imaging Library）：这里使用 Pillow 库，来进行图片创建、绘制文字以及保存图片，从而实现试卷的可视化。

环境配置及终端指令

或者也可以通过 pip 安装相关库：

二、Fraction 类使用方法详解

1. 使用两个整数创建分数

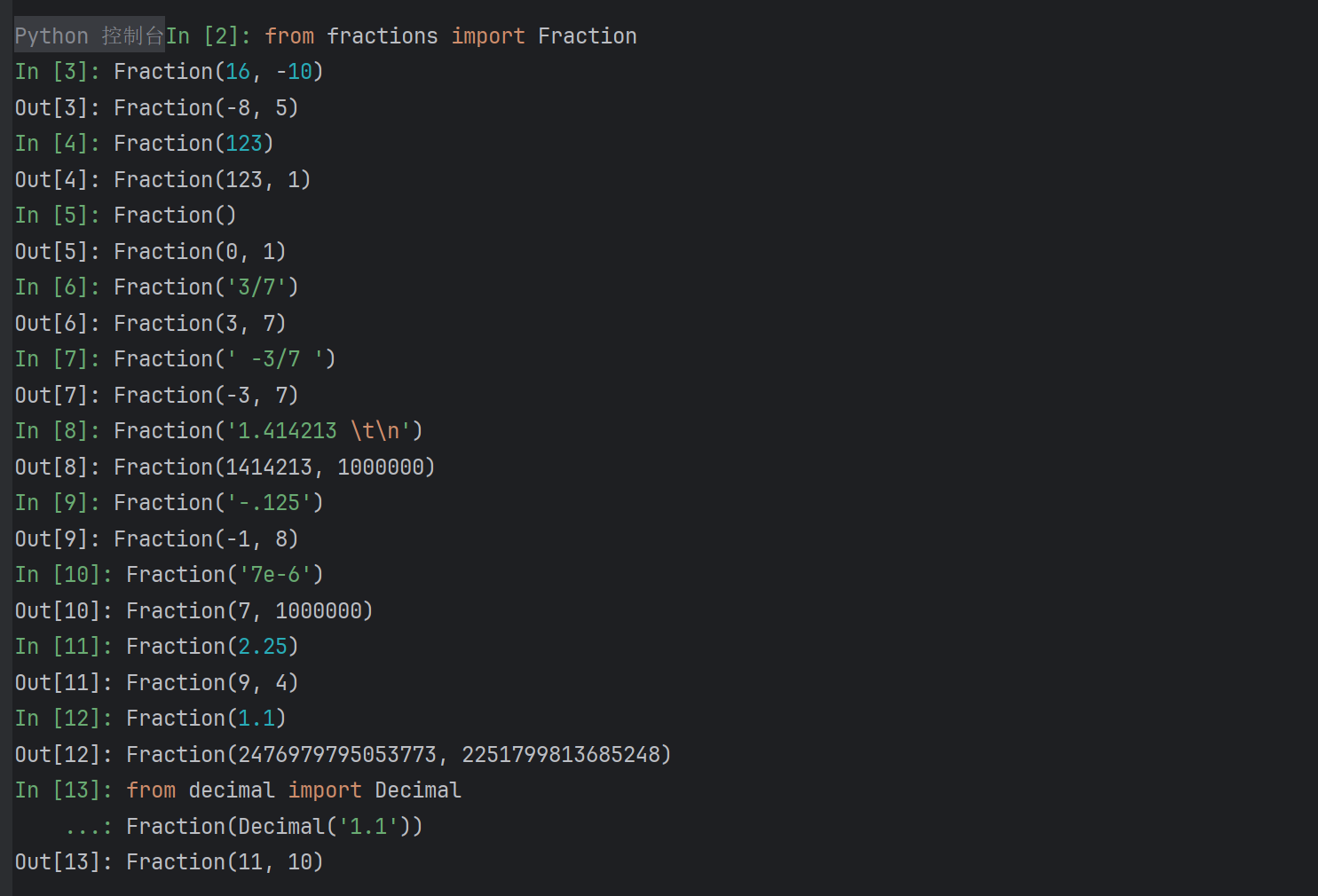
上述代码中，传入分子 16 和分母 -10，Fraction 会自动对分数进行约分和符号调整，结果为 Fraction(-8, 5)。这种方式是最直观的构造方法，适合我们手动设置分子和分母的情况。

2. 单参数形式

如果只提供一个参数，则默认分母为 1：

输出结果为 Fraction(123, 1)，适合需要将整数转换为分数的场景。

3. 无参数形式

如果不提供任何参数，Fraction 默认创建 0/1 的分数对象：

4. 以字符串形式传入分数

通过字符串传入分数，可以让 Fraction 自动解析其中的数字和符号。例如：

5. 带空格与负号的分数字符串

Fraction 能够解析包含空格或负号的字符串，如：

6. 解析包含其它字符的字符串

如果字符串中混有其他不可见字符（如制表符、换行符），Fraction 会自动去除多余空白并解析数字。例如：

输出为 Fraction(1414213, 1000000)，将浮点数转换为分数的形式。

7. 解析小数与负小数

8. 支持科学计数法

9. 使用浮点数创建分数

直接传入浮点数时，Fraction 会将其转换为最接近的分数表示，但这可能会引入浮点数本身的精度问题。例如：

这正是由于浮点数 1.1 无法精确表示而产生的误差。

11. 使用 Decimal 对象解决精度问题

为避免上述精度损失，可以使用 Decimal 模块创建高精度数字，然后传入 Fraction：

这样就能准确地表示 1.1 对应的分数，避免了浮点数误差问题。

三、实现分数四则运算试卷的全过程

点击Python Fraction类实战：生成小学分数四则运算试卷阅读全文