Python光学仿真举例---牛顿环

内容来自微信公众号小小光08

利用普通光源获得相干光的方法是，把由光源上同一点发出的光设法分成两部分，然后再使这两部分叠起来。由于这两部分光的相应部分实际上都来自同一发光原子的同一次发光，所以它们将满足相干条件而成为相干光。

获得相干光的方法有两种，一种叫分波阵面法，另一种叫分振幅法。

牛顿环是一种用分振幅方法实现的等厚干涉现象

如上图所示，平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加，若以平行单色光垂直照射到牛顿环上，则经空气层上、下表面反射的二光束存在光程差，它们在平凸透镜的凸面相遇后，将发生干涉。

从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环，如上如图所示，称为牛顿环。由于同一干涉环上各处的空气层厚度是相同的，因此它属于等厚干涉。

如设透镜的曲率半径为R，与接触点O相距为r处空气层的厚度为d，其几何关系式为

由于R≫d，可以略去d2得

光线应是垂直入射的，计算光程差时还要考虑光波在平玻璃板上反射会有半波损失，从而带来λ/2的附加光程差，所以总光程差为

产生暗环的条件是

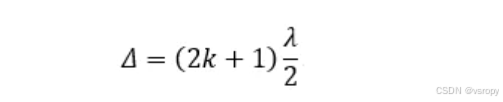
上式中，k=0，1，2，3，…为干涉暗条纹的级数。

第k级暗环的半径为

由上式可知，如果单色光源的波长λ已知，测出第m 级的暗环半径rm，即可得出平凸透镜的曲率半径R；反之，如果R已知，测出rm后，就可计算出入射单色光波的波长λ。

但是，用此测量关系式往往误差很大，原因在于凸面和平面不可能是理想的点接触；接触压力会引起局部形变，使接触处成为一个圆形平面，干涉环中心为一暗斑。或者空气间隙层中有了尘埃，附加了光程差，干涉环中心为一亮（或暗）斑，均无法确定环的几何中心。实际测量时，我们可以通过测量距中心较远的两个暗环的半径rm和rn的平方差来计算曲率半径R。

透镜的曲率半径为R=100mm，波长为500um时，牛顿环的明暗条纹，用Python脚本实现如下：

import numpy as np
import matplotlib.pyplot as plt


def newtons_rings(lam=500e-9, R=0.1):
    # 定义函数newtons_rings，用于生成牛顿环图样
    # lam: 波长，单位为米（默认值为500纳米，即500e-9米）
    # R: 曲率半径，单位为米（默认值为0.1米）

    # 计算y轴的最大值ym，这个值决定了模拟图样的尺寸
    # 根据牛顿环的原理，图样大小与波长、曲率半径有关
    ym = np.sqrt(10 * lam * R)

    # 在x和y方向上生成从-ym到ym的1001个点，用于构建网格
    xs = np.linspace(-ym, ym, 1001)
    ys = np.linspace(-ym, ym, 1001)

    # 使用meshgrid函数生成网格，X和Y分别是网格的x和y坐标
    X, Y = np.meshgrid(xs, ys)

    # 计算网格上每个点到原点的距离r
    r = np.sqrt(X ** 2 + Y ** 2)

    # 计算光强I，根据牛顿环的干涉原理
    # 干涉图样由余弦平方函数描述，其中相位差与r^2/R和波长lam有关
    I = (np.cos(np.pi * (r ** 2 / R + lam / 2) / lam)) ** 2

    # 将光强I转换为灰度值B，用于绘图
    # 这里简单地将I除以4并乘以255，将值域映射到0-255范围内
    # 注意：这种转换方式并不完全准确，因为实际的光强到灰度值的转换可能更复杂
    B = (I / 4.0) * 255

    # 使用matplotlib绘制牛顿环图样
    plt.figure(figsize=(10, 10))  # 设置图形大小
    plt.pcolormesh(X, Y, B, shading='gouraud', cmap='gray')  # 使用pcolormesh绘制彩色网格图
    # shading='gouraud'表示使用 Gouraud 阴影，cmap='gray'表示使用灰度颜色映射
    plt.title('Pattern of Newton\'s Rings')  # 设置标题
    plt.xlabel('x (mm)')  # 设置x轴标签
    plt.ylabel('y (mm)')  # 设置y轴标签
    plt.show()  # 显示图形


if __name__ == "__main__":
    newtons_rings()  # 调用函数newtons_rings，生成并显示牛顿环图样