前言
本文介绍c语言实现数据结构中的树的相关内容。
(【由浅入深】是一个系列文章,它记录了我个人作为一个小白,在学习c++技术开发方向计相关知识过程中的笔记,欢迎各位彭于晏刘亦菲从中指出我的错误并且与我共同学习进步,作为该系列的第一部曲-c语言,大部分知识会根据本人所学和我的助手——通义,DeepSeek等以及合并网络上所找到的相关资料进行核实誊抄,每一篇文章都可能会因为一些错误在后续时间增删改查,因为该系列按照我的网络课程学习笔记形式编写,我会使用绝大多数人使用的讲解顺序编写,所以基础框架和大部分内容案例会与他人一样,基础知识不会过于详细讲述)
一 . 树概念及结构
1.1 树的定义
树是一种非线性的数据结构,它是由n(n≥0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树,也就是说它是根在上,而叶在下的。
关键特性:
- 有且仅有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成m(m>0)个互不相交的集合T1、T2、…、Tm,其中每个集合Ti(1≤i≤m)又是一棵结构与树类似的子树
- 树是递归定义的(树可以拆分为根和n棵子树,而这n棵子树的每棵又能拆分为根和n棵子树,即可以按照
根+n棵子树的模式拆分,就像俄罗斯套娃,一个套娃可以包含另一个小套娃,而那个小套娃又可以包含更小的套娃,直到最小的套娃。树的结构也是这样,一个树可以包含子树,而子树本身也是树。)
重要注意:树形结构中,子树之间不能有交集,即树的结构中不能产生环,否则就不是树形结构。
1.2 树的基本特征
- 有限性:树中结点个数是有限的
- 层次性:树具有明显的层次关系
- 唯一性:
- 有且仅有一个根结点
- 除根结点外,每个结点有且仅有一个父结点
- 数量关系:一棵N个结点的树有
N-1条边
1.3 树的相关概念
A
/|\
/ | \
B C D
/ \ / \
E F G H
- 结点的度:一个节点含有的子树的个数。如A的度为3
- 叶子节点/终端节点:度为0的节点(如E、F、G、H)。没有子树的节点
- 非终端节点/分支节点:度不为0的节点(如A、B、C、D)。有子树的节点
- 双亲结点/父结点:若一个节点含有子节点,则这个节点称为其子节点的双亲结点(如A是B、C、D的父结点)
- 孩子节点/子节点:一个节点含有的子树的根节点(如B是A的孩子节点)
- 兄弟节点:具有相同父节点的节点互称为兄弟节点(如B、C、D是兄弟节点)
- 树的度:树中各结点的度的最大值(上例中树的度为3)
- 结点的层次:从根开始定义,根为第1层,根的孩子为第2层,以此类推
- 树的高度/深度:树中结点的最大层次(上例中树的高度为3)
- 祖先结点:从根到该结点所经分支上的所有结点(如A是所有结点的祖先)
- 子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙(如所有结点都是A的子孙)
- 森林:由m(m>0)棵互不相交的树的集合称为森林
1.4 树的表示方法
树的三种表示方法(双亲表示法、孩子表示法、孩子兄弟表示法)原本是为多叉树设计的,不能直接用于表示二叉树,需要改变指针的含义才能正确使用
树由于不是线性结构,存储表示相对复杂,常见的表示方法有:
1. 双亲表示法:用数组存储结点,每个结点记录其双亲结点的索引
-
核心思想:每个节点记住自己的父亲是谁
-
结构实现: 每个节点包含两个信息:
- 节点数据(如字符’A’)
- 父节点在数组中的索引(-1表示根节点)
-
结构体示例:
// 树节点结构
typedef struct {
char data; // 节点数据
int parentIndex; // 父节点在数组中的索引
} TreeNode;
// 整棵树结构
typedef struct {
TreeNode nodes[MAX_SIZE]; // 存储所有节点
int nodeCount; // 节点数量
int rootIndex; // 根节点在数组中的位置
} Tree;
示例图:(来源于大话数据结构-程杰的演示图)
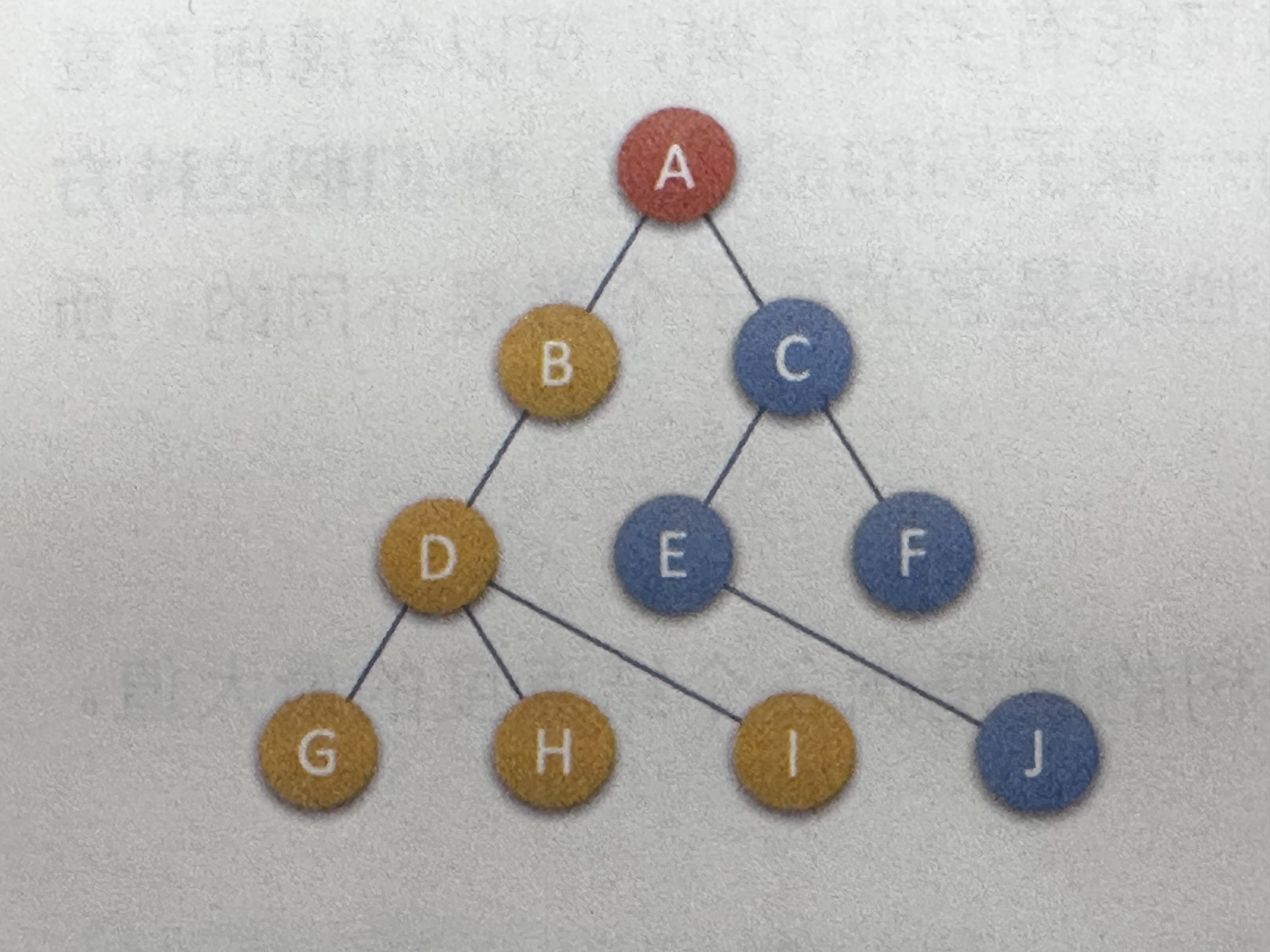
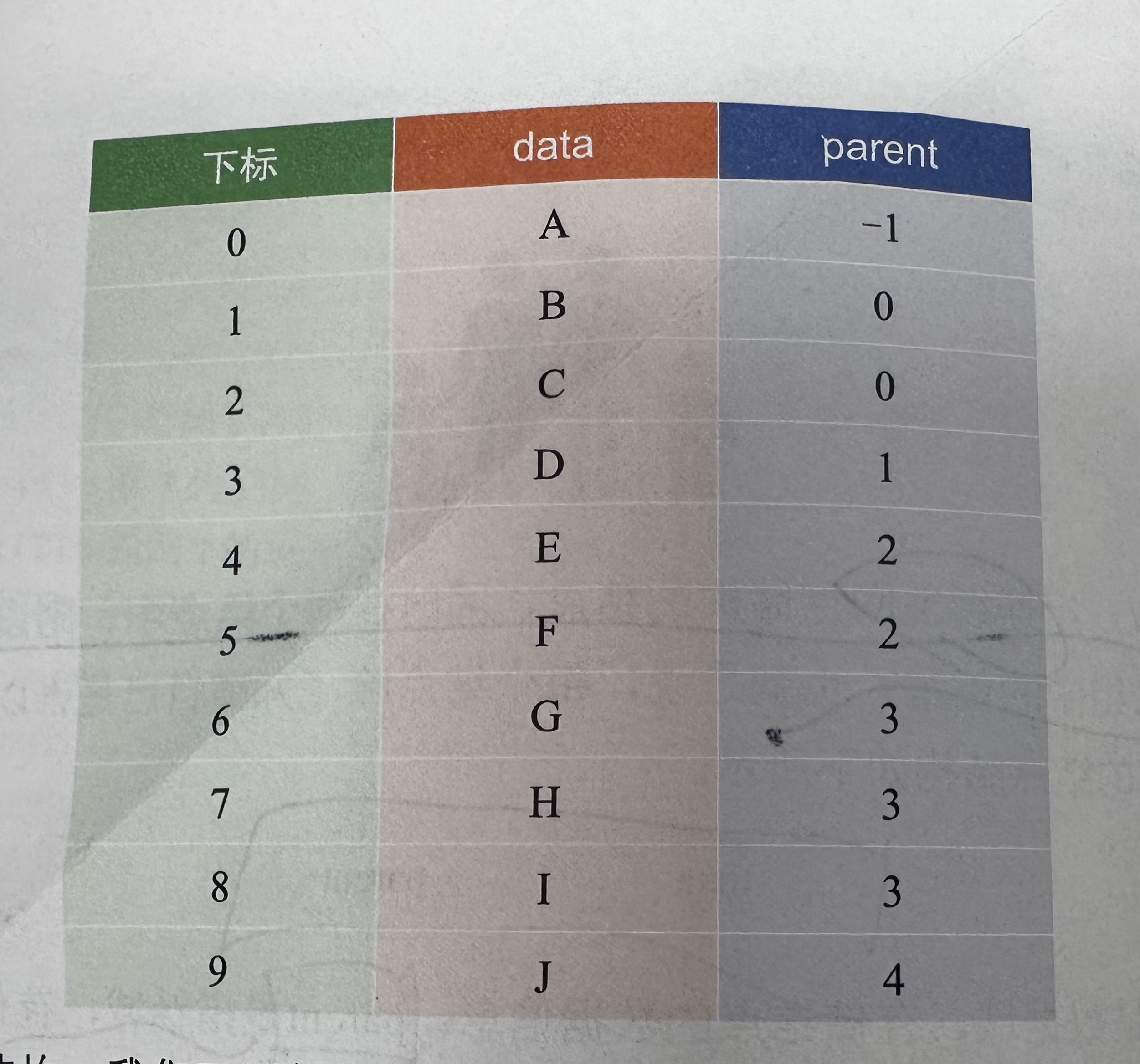
示例树:
A
/ \
B C
/ \ \
D E F
图形化描述:
想象一个表格,有三列:
- 索引:节点在数组中的位置(0开始)
- 数据:节点内容
- 父节点索引:父节点在数组中的位置
- 根节点的父节点索引为-1。
索引: 0 1 2 3 4 5
数据: A B C D E F
父索引:-1 0 0 1 1 2
-
工作原理:
- 根节点的
parentIndex = -1 - 其他节点的
parentIndex指向其父节点在数组中的位置 - 例如:节点B的父节点是A,那么B的
parentIndex就是A在数组中的索引
- 根节点的
-
特点:
- ✅ 查找父节点:O(1)时间
- ❌ 查找子节点:需要遍历整个数组
2. 孩子表示法:为每个结点建立一个孩子链表
-
核心思想:每个节点记住自己的所有孩子
-
结构实现: 每个节点包含两个信息:
- 节点数据
- 指向第一个孩子的指针(链表头指针)
-
结构体示例:
// 孩子链表节点
typedef struct CTNode {
int childIndex; // 孩子节点在数组中的位置
struct CTNode* next; // 指向下一个孩子
} *ChildPtr;
// 树节点
typedef struct {
char data; // 节点数据
ChildPtr firstChild; // 指向第一个孩子的指针
} CTBox;
// 整棵树
typedef struct {
CTBox nodes[MAX_SIZE]; // 存储所有节点
int nodeCount; // 节点数量
int rootIndex; // 根节点位置
} CTree;
示例图:(来源于大话数据结构-程杰的演示图)
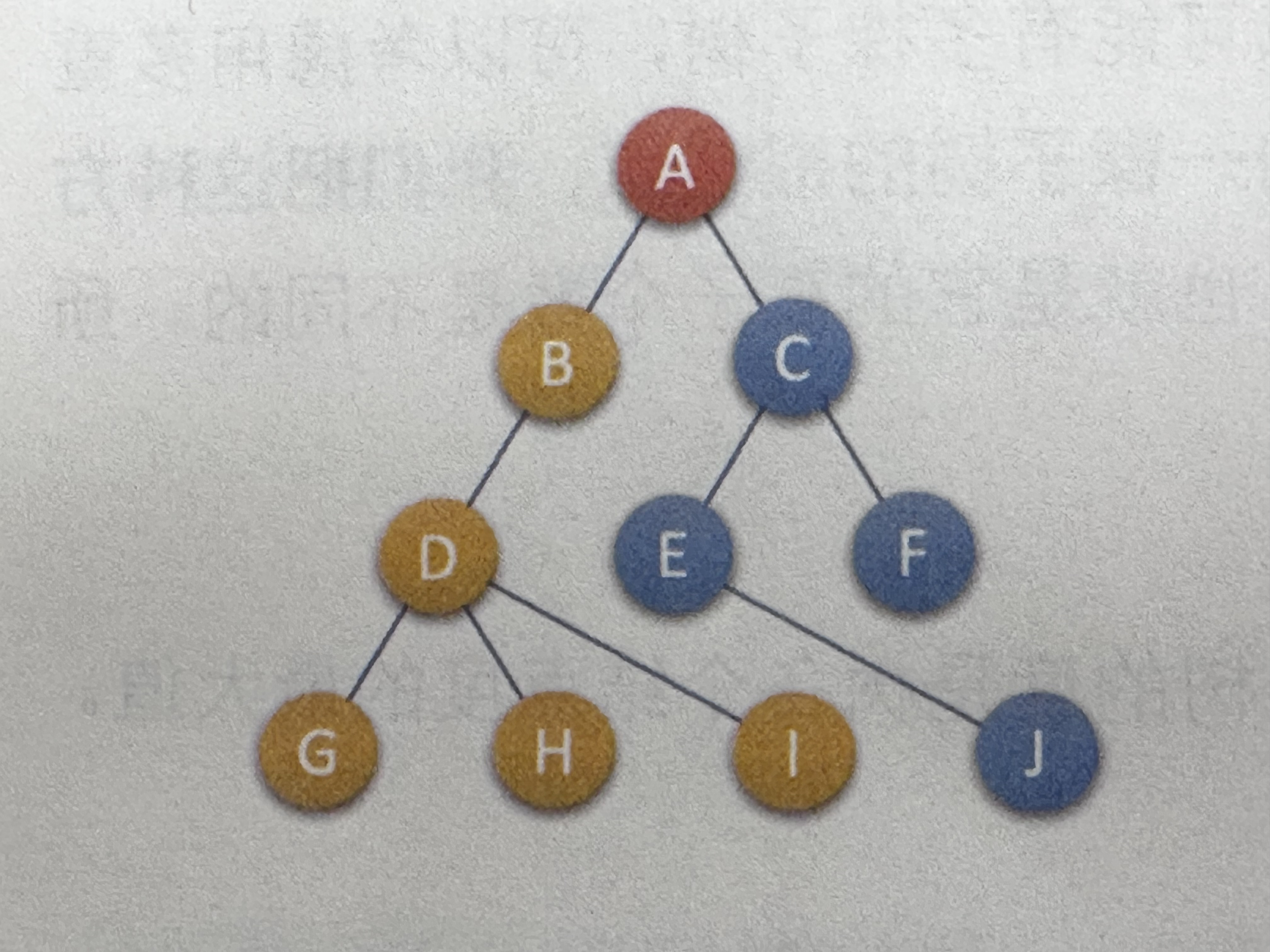
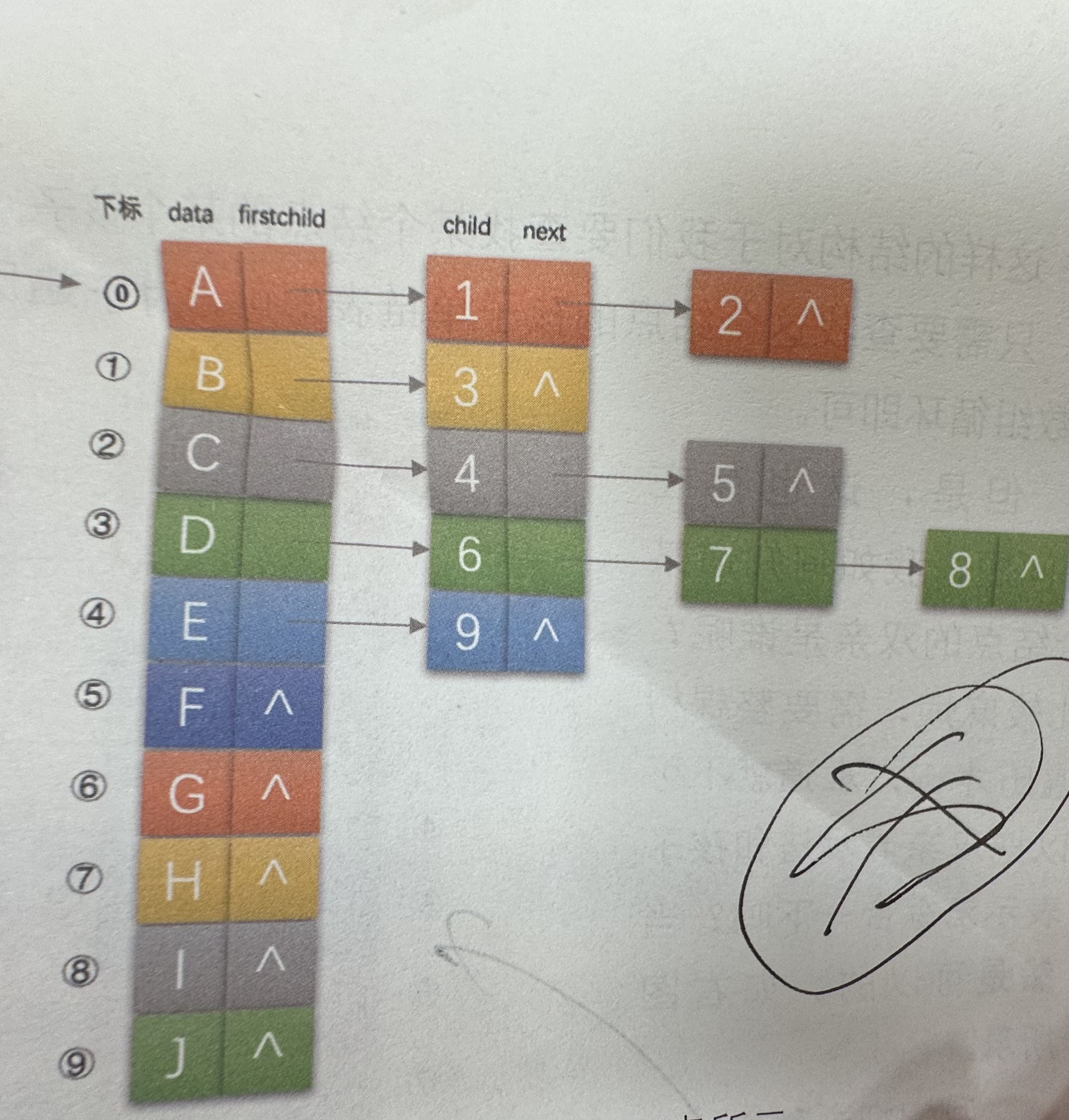
示例树:
A
/ \
B C
/ \ \
D E F
图形化描述:
想象每个节点有一个"第一个孩子"指针,孩子之间用链表连接。
A
|
B -> D
| \
E C -> F
-
工作原理:
- 每个节点通过
firstChild指针连接到其第一个孩子 - 通过孩子节点的
next指针连接到下一个兄弟孩子 - 例如:A节点有三个孩子B、C、D,那么A的
firstChild指向B,B的next指向C,C的next指向D
- 每个节点通过
-
特点:
- ✅ 查找子节点:O(1)时间(只需看第一个孩子,然后遍历链表)
- ❌ 查找父节点:需要遍历整个数组
3. 孩子兄弟表示法:用两个指针分别指向第一个孩子和下一个兄弟(最常用)
-
核心思想:将多叉树转化为二叉树表示
-
结构实现: 每个节点包含三个信息:
- 节点数据
- 指向第一个孩子的指针
- 指向下一个兄弟节点的指针
-
结构体示例:
typedef struct CSNode {
char val; // 节点值
struct CSNode* firstChild; // 指向第一个孩子
struct CSNode* nextSibling; // 指向下一个兄弟
} CSNode, *CSTree;
示例图:(来源于大话数据结构-程杰的演示图)
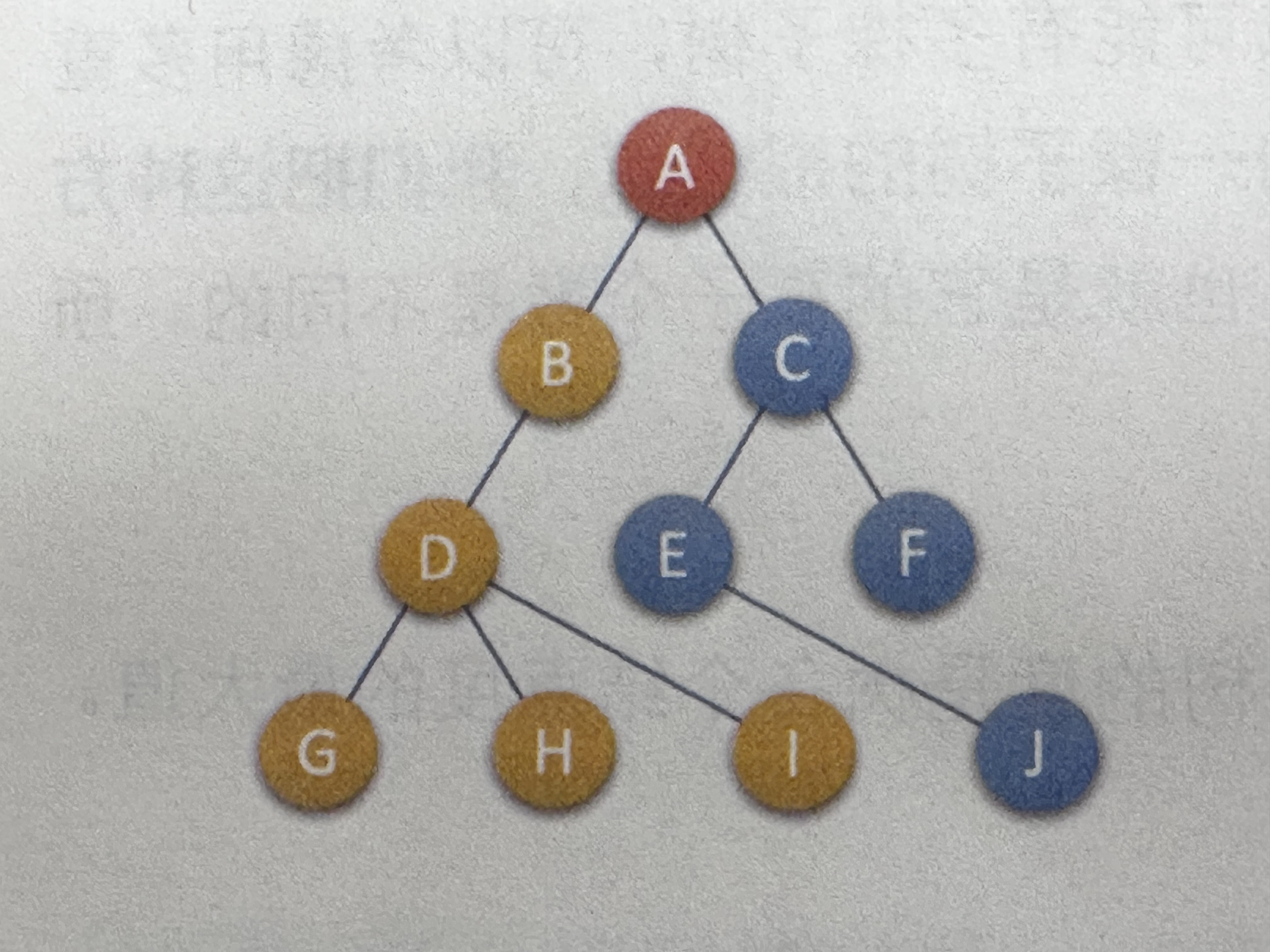
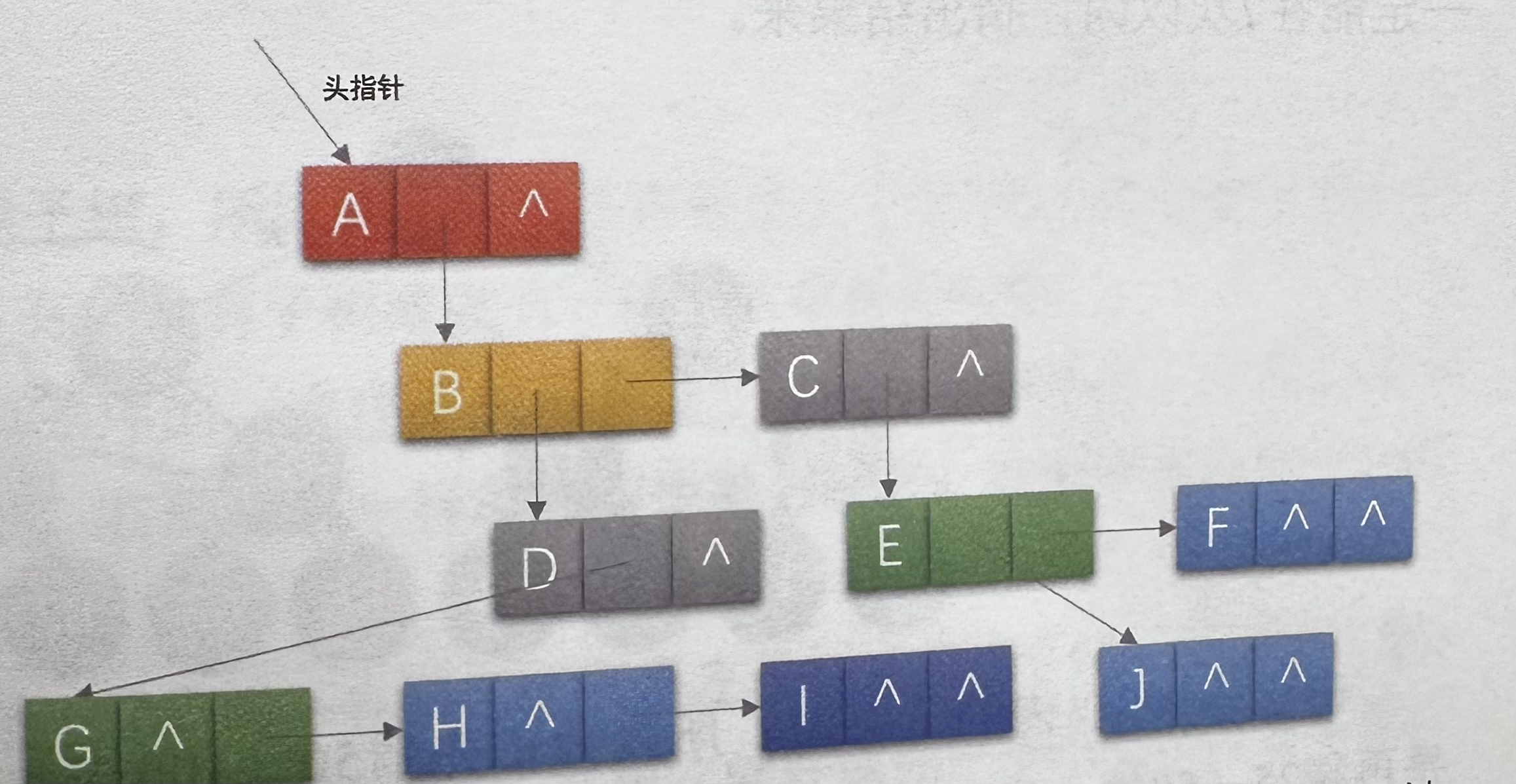
示例树:
A
/ \
B C
/ \ \
D E F
图形化描述:
想象每个节点有三个部分:
- 数据
- 指向第一个孩子的指针(firstChild)
- 指向下一个兄弟的指针(nextSibling)
A
|
B -> C
| \ \
D E F
-
工作原理:
firstChild指针指向该节点的第一个孩子nextSibling指针指向该节点的下一个兄弟(同级节点)- 例如:A节点有三个孩子B、C、D
- A的
firstChild指向B - B的
nextSibling指向C - C的
nextSibling指向D - D的
nextSibling为NULL
- A的
-
特点:
- ✅ 查找子节点:通过
firstChild快速找到第一个孩子,然后遍历链表 - ✅ 查找父节点:通过兄弟链表找到父节点(需要遍历兄弟链表)
- ✅ 可以将普通树转换为二叉树(左孩子右兄弟表示法)
- ✅ 查找子节点:通过
-
关键点:
- 孩子兄弟表示法是将多叉树转换为二叉树的最常用方法
- 转换规则:每个节点的
firstChild指向第一个孩子,nextSibling指向下一个兄弟 - 通过这种方式,任意一棵普通树都可以转化为唯一的一棵二叉树
二. 二叉树概念及结构
2.1 二叉树的定义
二叉树是n(n≥0)个结点的有限集合,该集合或为空集,或由一个根结点和两棵互不相交的、分别称为左子树和右子树的二叉树组成。
关键特点:
- 每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)
- 左子树和右子树是有顺序的,不能互换
- 二叉树是递归定义的
2.2 二叉树的基本形态
二叉树有五种基本形态:
- 空二叉树:如图1(a)
- 只有一个根节点的二叉树:如图1(b)
- 只有左子树:如图1(c)
- 只有右子树:如图1(d)
- 完全二叉树:如图1(e)
(a) (b) (c) (d) (e)
∅ A A A A
/ \ / \
B B B C
2.3 二叉树的特殊类型
满二叉树
A
/ \
B C
/ \ / \
D E F G
- 每一层的结点数都达到最大值
- 若树的深度为h,则结点总数为2^h - 1
完全二叉树
A
/ \
/ \
B C
/ \ /
D E F
- 除最后一层外,所有层都是满结点
- 最后一层只能缺右边连续结点
- 满二叉树是特殊的完全二叉树
二叉排序树(二叉查找树)
5
/ \
3 7
/ \ \
2 4 8
- 若左子树不为空,则左子树上所有结点的值均小于根结点的值
- 若右子树不为空,则右子树上所有结点的值均大于根结点的值
- 左、右子树也分别为二叉排序树
平衡二叉树(AVL树)
5
/ \
3 7
/ \
2 8
- 任意结点的左子树和右子树都是平衡二叉树
- 左子树和右子树的深度之差的绝对值不超过1
红黑树
- 在AVL树的平衡标准上进一步放宽条件
- 保证树的高度大致为log(n),平衡操作代价比AVL树小
2.4 二叉树的性质
-
若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2 i − 1 2^{i-1} 2i−1 个结点。
-
若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2 h − 1 2^h - 1 2h−1。
-
对任何一棵二叉树,如果度为0的叶结点个数为 n 0 n_0 n0,度为2的分支结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
-
若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log 2 ( n + 1 ) \log_2(n+1) log2(n+1)。
-
对于具有n个结点的
完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:-
若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点若i>0,【i位置节点的双亲序号: ⌊ ( i − 1 ) / 2 ⌋ \lfloor (i-1)/2 \rfloor ⌊(i−1)/2⌋(整数除法),自动向下取整】
-
若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
-
若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
-
为什么使用顺序结构:
- 普通的二叉树不适合用数组来存储,因为可能会存在大量空间浪费
- 完全二叉树更适合使用顺序结构存储
普通二叉树: 完全二叉树:
A A
/ \ / \
B C B C
/ \ / \
D E D E
普通二叉树存储:[A, B, C, null, null, D, E](浪费了2个空间)
完全二叉树存储:[A, B, C, D, E](没有空间浪费)
2.6 堆的概念
注意:这里所说的"堆"和操作系统虚拟进程地址空间中的"堆"是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
堆(Heap)是一种特殊的完全二叉树,它具有以下特性:
- 大堆:在二叉树中所有父结点均比子结点所代表的数值大(仅针对任意一个节点和它的两个子节点而言)
- 小堆:在二叉树中所有父结点均比子结点所代表的数值小
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
堆的基本操作
- 向上调整算法:用于堆的插入
- 向下调整算法:用于堆的删除和建堆
2.6.1 堆的实现完整代码示例
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<string.h>
// 定义堆中存储的数据类型(此处为整型)
typedef int HPDataType;
// 堆的数据结构定义
typedef struct Heap
{
HPDataType* a; // 指向堆数组的指针
int size; // 当前堆中元素个数
int capacity; // 堆的容量(数组大小)
}HP;
// 函数声明(堆的初始化、销毁、插入、删除等操作)
// 初始化堆结构(将堆的成员置为初始状态)
void HPInit(HP* php);
// 用数组初始化堆(同时完成建堆操作)
void HPInitArray(HP* php, HPDataType* a, int n);
// 销毁堆(释放内存并重置状态)
void HPDestroy(HP* php);
// 向堆中插入元素(保持堆性质)
void HPPush(HP* php, HPDataType x);
// 获取堆顶元素(最大值,大根堆)
HPDataType HPTop(HP* php);
// 删除堆顶元素(并保持堆性质)
void HPPop(HP* php);
// 判断堆是否为空
bool HPEmpty(HP* php);
// 辅助函数:向上调整(用于插入后保持堆性质)
void AdjustUp(HPDataType* a, int child);
// 辅助函数:向下调整(用于删除后保持堆性质)
void AdjustDown(HPDataType* a, int n, int parent);
// 初始化堆结构(将堆的成员置为初始状态)
void HPInit(HP* php)
{
assert(php); // 确保传入的指针有效
php->a = NULL; // 初始时数组指针为空
php->size = 0; // 元素个数为0
php->capacity = 0; // 容量为0
}
// 用数组初始化堆(同时完成建堆操作)
void HPInitArray(HP* php, HPDataType* a, int n)
{
assert(php); // 确保传入的指针有效
// 为堆数组分配内存(大小为n)
php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
perror("malloc fail"); // 内存分配失败处理
return;
}
// 复制数组内容到堆数组
memcpy(php->a, a, sizeof(HPDataType) * n);
php->capacity = php->size = n; // 设置容量和当前元素个数
// 建堆操作(关键优化:使用向下调整建堆,时间复杂度O(N))
// 1. 从最后一个非叶子节点开始(索引为(n-1-1)/2)
// 2. 依次向上调整每个节点
for (int i = (php->size-1 - 1)/2; i >= 0; i--)
{
AdjustDown(php->a, php->size, i);
}
}
// 销毁堆(释放内存并重置状态)
void HPDestroy(HP* php)
{
assert(php); // 确保传入的指针有效
free(php->a); // 释放堆数组内存
php->a = NULL; // 避免悬空指针
php->capacity = 0; // 重置容量
php->size = 0; // 重置元素个数
}
// 交换两个元素的值
void Swap(HPDataType* px, HPDataType* py)
{
HPDataType tmp = *px; // 临时存储px的值
*px = *py; // 将py的值赋给px
*py = tmp; // 将临时值赋给py
}
// 向上调整:从child位置开始,将元素上浮到合适位置(保持大根堆性质)
// 1. 计算父节点索引((child-1)/2)
// 2. 当child>0且当前元素大于父元素时,交换
// 3. 继续向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while(child > 0) // 当child不是根节点时
{
if (a[child] > a[parent]) // 如果当前元素大于父元素
{
Swap(&a[child], &a[parent]); // 交换
child = parent; // 更新child为父节点
parent = (parent - 1) / 2; // 计算新的父节点
}
else
{
break; // 已满足堆性质,退出
}
}
}
// 向下调整:从parent位置开始,将元素下沉到合适位置(保持大根堆性质)
// 1. 计算左孩子索引(parent*2+1)
// 2. 找到左右孩子中较大的那个(如果存在)
// 3. 如果较大孩子大于父节点,则交换并继续下沉
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1; // 左孩子索引
while (child < n) // 当孩子索引在数组范围内
{
// 1. 检查右孩子是否存在且比左孩子大
if (child+1 < n && a[child + 1] > a[child])
{
++child; // 选择右孩子
}
// 2. 如果当前孩子大于父节点,则交换
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child; // 更新父节点为当前孩子
child = parent * 2 + 1; // 计算新的孩子索引
}
else
{
break; // 已满足堆性质,退出
}
}
}
// 向堆中插入元素(保持堆性质)
void HPPush(HP* php, HPDataType x)
{
assert(php); // 确保堆有效
// 1. 检查容量是否足够,不够则扩容
if (php->size == php->capacity)
{
// 扩容策略:初始容量为0则设为4,否则翻倍
size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
// 重新分配内存
HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail"); // 扩容失败处理
return;
}
php->a = tmp; // 更新数组指针
php->capacity = newCapacity; // 更新容量
}
// 2. 将新元素放入堆尾
php->a[php->size] = x;
php->size++; // 元素个数+1
// 3. 从新元素位置向上调整
AdjustUp(php->a, php->size-1);
}
// 获取堆顶元素(最大值,大根堆)
HPDataType HPTop(HP* php)
{
assert(php); // 确保堆有效
assert(php->size > 0); // 确保堆非空
return php->a[0]; // 堆顶元素(大根堆的根节点)
}
// 删除堆顶元素(并保持堆性质)
void HPPop(HP* php)
{
assert(php); // 确保堆有效
assert(php->size > 0); // 确保堆非空
// 1. 交换堆顶和堆尾元素
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--; // 元素个数-1(堆尾元素被删除)
// 2. 从根节点开始向下调整
AdjustDown(php->a, php->size, 0);
}
// 判断堆是否为空
bool HPEmpty(HP* php)
{
assert(php); // 确保堆有效
return php->size == 0; // 元素个数为0则为空
}
// 堆排序(升序排列)
void HeapSort(int* a, int n)
{
// 1. 建堆(使用向下调整法,时间复杂度O(N))(建堆后(无论是大顶堆还是小顶堆)不能保证整个数组是升序或降序的,
//只能保证父节点与子节点之间的大小关系)
// 从最后一个非叶子节点开始(索引(n-1-1)/2)向根节点调整
for (int i = (n-1-1)/2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
// 2. 排序过程
// 1) 将堆顶(最大值)与堆尾交换
// 2) 缩小堆范围(堆大小-1)
// 3) 从根节点向下调整
int end = n - 1; // 堆尾索引
while (end > 0)
{
Swap(&a[0], &a[end]); // 交换最大值到堆尾
AdjustDown(a, end, 0); // 从根节点向下调整(堆大小为end)
--end; // 缩小堆范围
}
}
int main()
{
int a[] = { 60,70,65,50,32,100 };
HP hp;
HPInit(&hp);
for (int i = 0; i < sizeof(a)/sizeof(int); i++)
{
HPPush(&hp, a[i]);
}
while (!HPEmpty(&hp))
{
printf("%d\n", HPTop(&hp));
HPPop(&hp);
}
HPDestroy(&hp);
return 0;
}
2.6.2 堆的存储结构
typedef int HPDataType;
typedef struct Heap {
HPDataType* a; // 堆
int size; // 堆的大小
int capacity; // 堆的容量
} HP;
2.6.3 堆的节点关系(数组存储)
对于具有n个结点的完全二叉树,如果按照从上至下、从左至右的数组顺序对所有结点从0开始编号,对于序号为i的结点有:
- 若i > 0,i位置结点的双亲序号为:(i-1)/2
- 若2i+1 < n,左孩子序号:2i+1
- 若2i+2 < n,右孩子序号:2i+2
2.6.4 堆的实现算法
向上调整算法
void AdjustUp(HPDataType* a, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (a[child] < a[parent]) { // 小堆
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
} else {
break;
}
}
}
向下调整算法
void AdjustDown(HPDataType* a, int n, int parent) {
int child = 2 * parent + 1; // 左孩子
while (child < n) {
// 找到左右孩子中较小的一个
if (child + 1 < n && a[child + 1] < a[child]) {
child++;
}
// 如果孩子比父节点小,交换
if (a[child] < a[parent]) {
swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
} else {
break;
}
}
}
堆的创建(建堆)
void HeapCreate(HP* php, HPDataType* a, int size) {
php->a = (HPDataType*)malloc(sizeof(HPDataType) * size);
memcpy(php->a, a, sizeof(HPDataType) * size);
php->size = size;
php->capacity = size;
// 从最后一个非叶子节点开始调整
for (int i = (size - 2) / 2; i >= 0; i--) {
AdjustDown(php->a, size, i);
}
}
堆的插入
void HeapPush(HP* php, HPDataType x) {
// 扩容
if (php->size == php->capacity) {
php->capacity *= 2;
php->a = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity);
}
// 插入到数组末尾
php->a[php->size] = x;
php->size++;
// 向上调整
AdjustUp(php->a, php->size - 1);
}
动画演示:
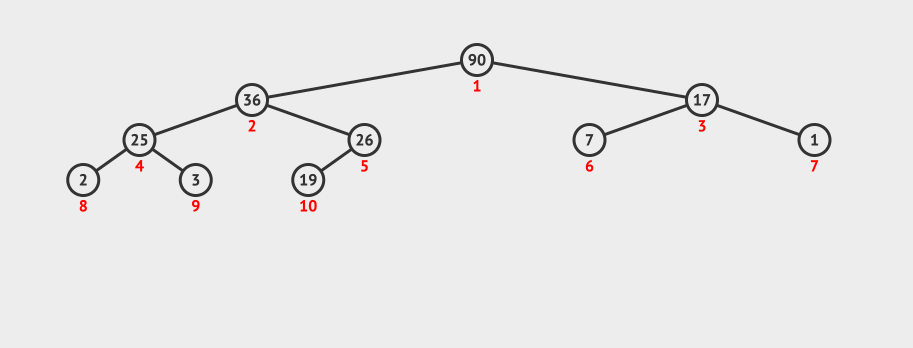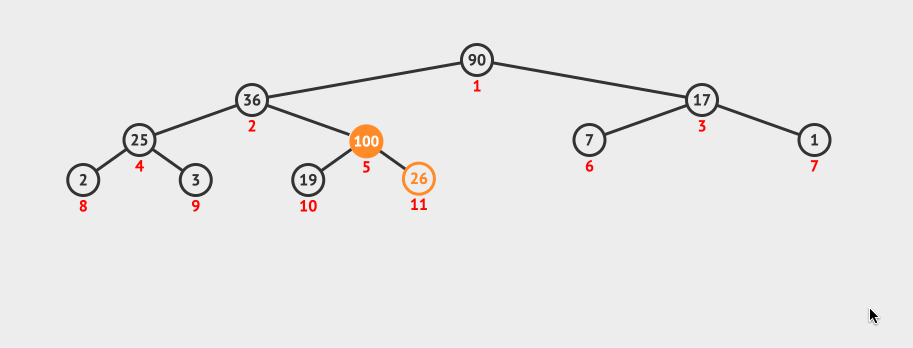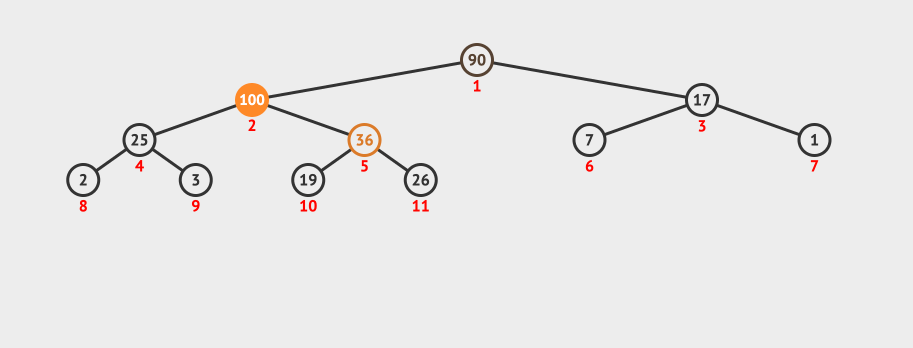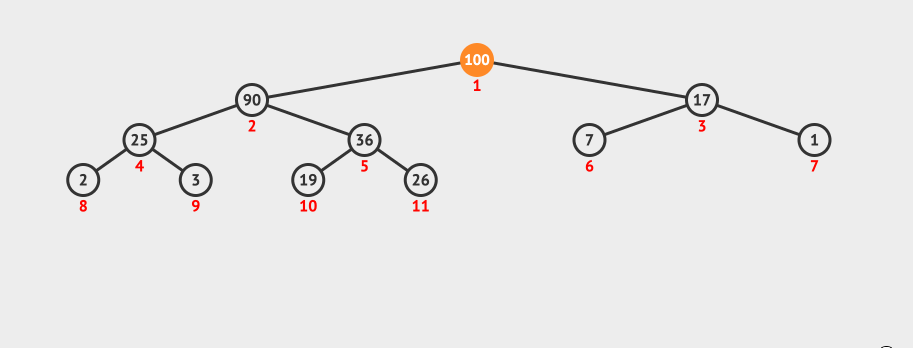
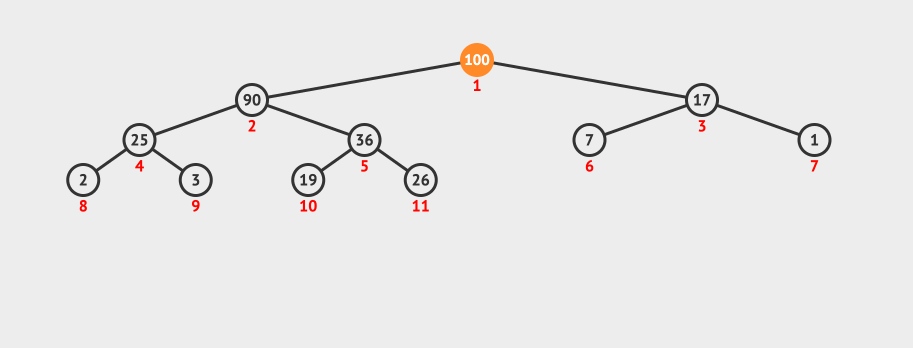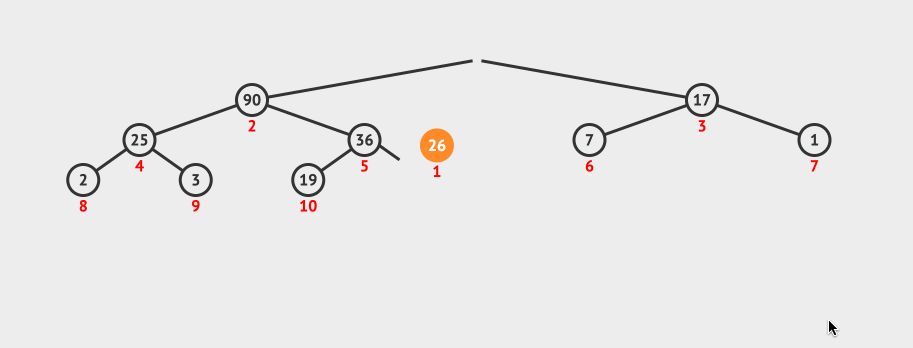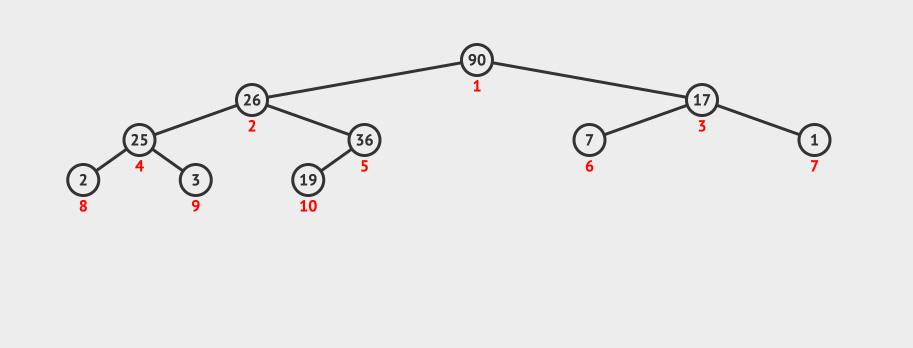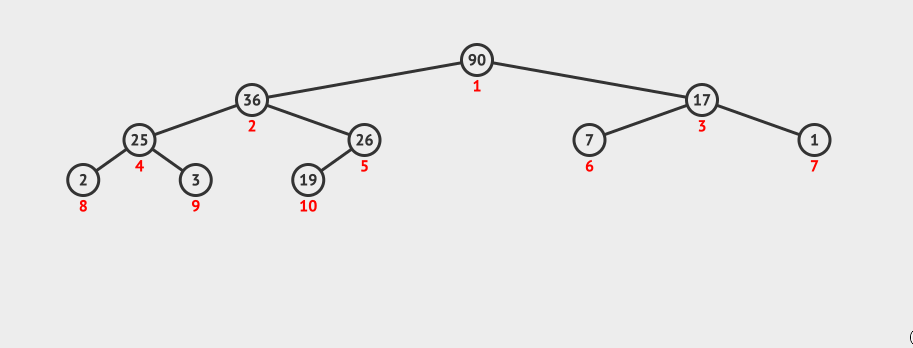
堆的删除
void HeapPop(HP* php) {
// 交换堆顶和最后一个元素
swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
// 向下调整
AdjustDown(php->a, php->size, 0);
}
动画演示:
2.6.6 堆的应用
1. 堆排序
基本概念
堆排序(Heapsort)是一种基于堆数据结构的排序算法。堆是一种特殊的完全二叉树,分为:
- 大顶堆:父节点值 ≥ 子节点值(根节点为最大值)
- 小顶堆:父节点值 ≤ 子节点值(根节点为最小值)
堆排序原理与步骤
-
核心思想
将数组构建成大顶堆(或小顶堆),堆顶元素始终是最大(或最小)元素,通过重复交换堆顶与堆尾元素并调整堆结构实现排序。 -
具体步骤
- 构建初始堆:将待排序数组构建成大顶堆
- 从最后一个非叶子节点开始,自底向上进行"向下调整"(heapify)
- 时间复杂度:O(n)
- 重复提取:
- 交换堆顶元素与堆末尾元素
- 缩小堆的大小(排除已排序部分)
- 调整剩余元素为堆结构
- 重复此过程,直到堆大小为1
-
代码实现
void max_heapify(int arr[], int start, int end) {
int dad = start;
int son = dad * 2 + 1;
while (son <= end) {
if (son + 1 <= end && arr[son] < arr[son + 1])
son++;
if (arr[dad] > arr[son])
return;
else {
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
// 构建初始堆
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 重复提取
for (int i = len - 1; i > 0; i--) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}
堆排序的特性分析
| 特性 | 说明 | 详细解释 |
|---|---|---|
| 时间复杂度 | O(n log n) | 构建堆O(n),每次调整堆O(log n),共n次调整 |
| 空间复杂度 | O(1) | 原地排序,只需常数级额外空间 |
| 稳定性 | 不稳定 | 相等元素的相对顺序可能改变 |
| 优点 | 1. 时间复杂度稳定 2. 空间效率高 3. 适合大规模数据 | 无论输入数据如何,时间复杂度都保持O(n log n) |
| 缺点 | 1. 实现相对复杂 2. 不适合小规模数据 3. 常数因子较大 | 对于小规模数据,构建堆的开销可能超过插入排序 |
堆排序的应用场景
-
大数据量排序:
- 当需要对大量数据进行排序时,堆排序的O(n log n)时间复杂度使其成为理想选择
- 例如:数据库索引排序、大规模日志分析
-
嵌入式系统:
- 由于是原地排序算法,只需要常数级的额外空间
- 适合内存受限的环境,如嵌入式设备、物联网设备
-
需要稳定时间复杂度的场景:
- 堆排序在最坏情况下也有O(n log n)的时间复杂度
- 适合对最坏情况有严格要求的系统,如金融交易系统
2.TOP-K问题
TOP-K问题定义
TOP-K问题是指在数据集中找出前K个最大(或最小)的元素。常见应用场景: 专业前10名, 世界500强企业,富豪榜,游戏中前100的活跃玩家,搜索引擎中的热门关键词
堆解决TOP-K问题的原理
-
核心思想
- 求前K个最大元素:构建小顶堆(堆顶是最小的)
- 求前K个最小元素:构建大顶堆(堆顶是最大的)
-
解决步骤
-
用数据集合中前K个元素建立堆
- 求前K大:建立小顶堆
- 求前K小:建立大顶堆
-
用剩余的N-K个元素依次与堆顶元素比较
- 如果满足条件(例如,求前K大,当前元素 > 堆顶),则替换堆顶元素
-
将剩余N-K个元素与堆顶比较完毕后,堆中剩余的K个元素即为所求
-
ai版本
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// 交换两个整数
void Swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
// 小顶堆调整(确保堆顶为最小值)
void AdjustDown(int* heap, int k, int root) {
int child = root * 2 + 1; // 左孩子索引
while (child < k) {
// 找到左右孩子中较小的
if (child + 1 < k && heap[child + 1] < heap[child]) {
child++; // 指向较小的孩子
}
// 如果当前节点比孩子大,交换
if (heap[root] > heap[child]) {
Swap(&heap[root], &heap[child]);
root = child; // 继续向下调整
child = root * 2 + 1;
} else {
break; // 已满足小顶堆性质
}
}
}
// 生成随机数据文件(10万条数据)
void CreateRandomData(const char* filename, int n) {
srand(time(0));
FILE* fp = fopen(filename, "w");
if (!fp) {
perror("File open error");
exit(1);
}
for (int i = 0; i < n; i++) {
int num = rand() % 1000000; // 0~999999
fprintf(fp, "%d\n", num);
}
fclose(fp);
}
// 求TopK问题(最大K个数)
void TopK(const char* filename, int k) {
FILE* fp = fopen(filename, "r");
if (!fp) {
perror("File open error");
return;
}
// 1. 创建大小为k的小顶堆
int* min_heap = (int*)malloc(sizeof(int) * k);
if (!min_heap) {
perror("Memory allocation error");
fclose(fp);
return;
}
// 2. 读取前k个元素
for (int i = 0; i < k; i++) {
fscanf(fp, "%d", &min_heap[i]);
}
// 3. 建立小顶堆(堆顶为最小值)
for (int i = (k - 1) / 2; i >= 0; i--) {
AdjustDown(min_heap, k, i);
}
// 4. 处理剩余数据
int num;
while (fscanf(fp, "%d", &num) != EOF) {
// 如果当前数比堆顶大,替换堆顶并调整
if (num > min_heap[0]) {
min_heap[0] = num;
AdjustDown(min_heap, k, 0);
}
}
fclose(fp);
// 5. 输出结果(从大到小排序)
printf("Top %d numbers: ", k);
for (int i = k - 1; i >= 0; i--) {
// 从堆底到堆顶(大到小)
printf("%d ", min_heap[i]);
}
printf("\n");
free(min_heap);
}
int main() {
// 生成测试数据(10万条)
CreateRandomData("data.txt", 100000);
// 测试TopK
int k = 10;
printf("Finding Top %d numbers...\n", k);
TopK("data.txt", k);
return 0;
}
实现示例(求前K大元素)
// 生成随机数据文件
void CreateNDate()
{
int n = 100000; // 数据量
srand(time(0)); // 初始化随机种子
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error"); // 文件打开失败处理
return;
}
// 生成随机数据并写入文件
for (int i = 0; i < n; ++i)
{
// 保证数据范围在0-999999之间
int x = (rand() + i) % 1000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
void topk() {
CreateNData(); // 创建随机数据
int k;
printf("请输入k值: ");
scanf_s("%d", &k);
const char *file = "data.txt";
FILE *fout = fopen(file, "r");
if (fout == NULL) {
perror("fopen error");
return;
}
int *minheap = (int *)malloc(sizeof(int) * k);
if (minheap == NULL) {
perror("malloc fail");
return;
}
// 读取前k个元素
for (int i = 0; i < k; i++)
fscanf_s(fout, "%d", &minheap[i]);
// 构建小顶堆
for (int i = (k-1-1)/2; i >= 0; i--)
AdjustDown(minheap, i, k);
int x;
// 处理剩余元素
while (fscanf_s(fout, "%d", &x) > 0) {
if (x > minheap[0]) {
minheap[0] = x;
AdjustDown(minheap, k, 0);
}
}
printf("最大前%d个数为\n", k);
for (int i = 0; i < k; i++)
printf("%d ", minheap[i]);
}
TOP-K问题的复杂度分析
| 指标 | 复杂度 | 说明 |
|---|---|---|
| 时间复杂度 | O(n log k) | 构建初始堆O(k),处理剩余n-k个元素,每个元素O(log k) |
| 空间复杂度 | O(k) | 只需存储K个元素 |
| 优势 | 相比排序法O(n log n) | 当k远小于n时,效率显著提升 |
TOP-K问题的应用场景
-
实时推荐系统:
- 在用户浏览过程中,实时维护热门商品的Top K列表
- 例如:电商网站的"今日最热商品"推荐
-
数据流处理:
- 当数据是流式输入时,可以使用堆来维护Top K
- 例如:实时监控系统中的"最活跃IP"列表
-
日志分析:
- 找出最频繁的错误代码或访问最多的URL
- 例如:网站访问日志中前100个最热门页面
-
电商应用:
- 找出最畅销的商品或最受欢迎的搜索关键词
- 例如:电商平台的"热销榜"、“热搜榜”
-
社交网络:
- 找出最活跃的用户或最受欢迎的内容
- 例如:微博的"热门话题"、“明星榜单”
TOP-K问题的其他解决方案对比
| 解决方案 | 时间复杂度 | 空间复杂度 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|---|---|
| 堆排序法 | O(n log k) | O(k) | K值较小的数据流处理 | 实现简单,效率高 | K值较大时效率降低 |
| 快速选择算法 | O(n)平均,O(n²)最坏 | O(1) | 内存受限的场景 | 平均时间复杂度低 | 最坏情况差,不稳定 |
| 计数排序法 | O(n) | O(range) | 数据范围已知且较小 | 时间复杂度低 | 空间消耗大 |
| MapReduce | O(n) | O(n) | PB级数据 | 水平扩展能力强 | 需要分布式环境 |
| 桶排序 | O(n) | O(n) | 数据分布均匀 | 接近线性时间 | 数据分布不均时效率低 |
三. 二叉树链式结构的实现
3.1 二叉树链式结构概述
基本概念: 二叉树链式存储结构是用链表来表示一棵二叉树,使用链表链接树节点。每个节点包含三个部分:
- 数据域:存储节点数据
- 左指针:指向左子节点
- 右指针:指向右子节点
链式结构的二叉树是递归定义的:一棵非空的二叉树由根节点、左子树和右子树组成,而左子树和右子树本身也是二叉树。
节点结构定义
typedef int BTDataType; // 定义数据类型,可根据需要修改
typedef struct BinaryTreeNode {
struct BinaryTreeNode* left; // 指向左子节点
struct BinaryTreeNode* right; // 指向右子节点
BTDataType data; // 节点存储的数据(BTDataType val;)
} BTNode;
注意:这里使用
struct BinaryTreeNode*而不是BTNode*,是因为在定义结构体时,结构体名称尚未完全定义,需要使用完整的结构体名进行指针声明。
节点申请函数
BTNode* BuyBTNode(int val) {
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL) {
perror("malloc fail");
return NULL;
}
newnode->data = val; // 设置节点数据
newnode->left = NULL; // 左子节点初始化为空
newnode->right = NULL; // 右子节点初始化为空
return newnode;
}
关键点:
- 内存分配失败处理:使用
perror输出错误信息 - 必须初始化左右指针为
NULL,避免野指针
3.2 二叉树的构建
1. 手动构建示例二叉树
BTNode* CreateTree() {
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
n1->left = n2; // 节点1的左子节点指向节点2
n1->right = n4; // 节点1的右子节点指向节点4
n2->left = n3; // 节点2的左子节点指向节点3
n4->left = n5; // 节点4的左子节点指向节点5
n4->right = n6; // 节点4的右子节点指向节点6
return n1; // 返回根节点
}
2. 二叉树结构示意图
1
/ \
2 4
/ / \
3 5 6
3.3 二叉树的遍历
二叉树遍历的定义
遍历二叉树是指按照特定规律访问二叉树中每个节点的过程,每个节点被访问且仅访问一次。根据根节点的访问时机,主要分为三种遍历方式:
| 遍历方式 | 访问顺序 | 递归实现公式 |
|---|---|---|
| 前序遍历 | 根->左->右 | NLR |
| 中序遍历 | 左->根->右 | LNR |
| 后序遍历 | 左->右->根 | LRN |
注意:“前序、中序、后序序列各有明确的前驱和后继关系定义”。
递归实现原理
二叉树的递归遍历基于递归思想:
- 递归终止条件:当前节点为NULL
- 递归关系:将问题分解为子问题(左子树、右子树)
- 操作时机:根据遍历方式决定访问根节点的时机
三种基本遍历方式的实现
(1) 前序遍历(根-左-右)
void PreOrder(BTNode* root) {
if (root == NULL) {
printf("N "); // 表示空节点
return;
}
printf("%d ", root->data); // 访问根节点
PreOrder(root->left); // 遍历左子树
PreOrder(root->right); // 遍历右子树
}
遍历过程分析:
- 访问根节点1 → 1
- 遍历左子树(以2为根)→ 访问2 → 遍历左子树(以3为根)→ 访问3 → 左右子树为空 → 返回
- 遍历右子树(以4为根)→ 访问4 → 遍历左子树(以5为根)→ 访问5 → 左右子树为空 → 返回
- 遍历右子树(以6为根)→ 访问6 → 左右子树为空 → 返回
前序遍历结果:1 2 3 N N 4 5 N N 6 N N
(2) 中序遍历(左-根-右)
void InOrder(BTNode* root) {
if (root == NULL) {
printf("N ");
return;
}
InOrder(root->left); // 遍历左子树
printf("%d ", root->data); // 访问根节点
InOrder(root->right); // 遍历右子树
}
遍历过程分析:
- 遍历左子树(以2为根)→ 遍历左子树(以3为根)→ 访问3 → 左右子树为空 → 返回
- 访问根节点2
- 遍历右子树(以NULL为根)→ 返回
- 访问根节点1
- 遍历右子树(以4为根)→ 遍历左子树(以5为根)→ 访问5 → 左右子树为空 → 返回
- 访问根节点4
- 遍历右子树(以6为根)→ 访问6 → 左右子树为空 → 返回
中序遍历结果:N 3 N 2 N 1 N 5 N 4 N 6 N
(3) 后序遍历(左-右-根)
void PostOrder(BTNode* root) {
if (root == NULL) {
printf("N ");
return;
}
PostOrder(root->left); // 遍历左子树
PostOrder(root->right); // 遍历右子树
printf("%d ", root->data); // 访问根节点
}
遍历过程分析:
- 遍历左子树(以2为根)→ 遍历左子树(以3为根)→ 访问3 → 左右子树为空 → 返回
- 访问根节点2
- 遍历右子树(以NULL为根)→ 返回
- 遍历右子树(以4为根)→ 遍历左子树(以5为根)→ 访问5 → 左右子树为空 → 返回
- 遍历右子树(以6为根)→ 访问6 → 左右子树为空 → 返回
- 访问根节点4
- 访问根节点1
后序遍历结果:N N 3 N 2 N N N 5 N N 6 N 4 N 1
(4) 层序遍历(广度优先遍历)
层序遍历是按层次从上到下、从左到右访问节点,需要借助队列实现。
具体步骤:(即出队一个,就将其所有子节点从左到右依次入队)
- 初始化:
- 创建一个队列
- 将根节点入队
- 循环处理(当队列不为空时):
a. 记录当前层节点数:levelSize = queue.size()
b. 创建临时列表:level = [],用于存储当前层的节点值
c. 处理当前层所有节点(循环levelSize次):- 出队一个节点:node = queue.poll()
- 访问该节点:level.add(node.val)
- 将该节点的左子节点(如果存在)入队:if (node.left != null) queue.offer(node.left)
- 将该节点的右子节点(如果存在)入队:if (node.right != null) queue.offer(node.right) d. 将当前层结果加入最终结果:result.add(level)
- 结束条件:当队列为空时,遍历结束
理解版本
// 层序遍历(Level Order Traversal)实现:按二叉树层次从上到下、从左到右遍历节点
// 使用队列辅助实现,通过队列存储待访问节点,确保层次顺序
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef struct BinTreeNode* QDataType;
typedef struct QueueNode
{
QDataType val;
struct QueueNode* next;
}QNode;
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;
void QueueInit(Queue* pq)
{
assert(pq);
pq->phead = NULL;
pq->ptail = NULL;
pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
// 入队列
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
return;
}
newnode->val = x;
newnode->next = NULL;
if (pq->ptail)
{
pq->ptail->next = newnode;
pq->ptail = newnode;
}
else
{
pq->phead = pq->ptail = newnode;
}
pq->size++;
}
// 出队列
void QueuePop(Queue* pq)
{
assert(pq);
// 0个节点
// 温柔检查
//if (pq->phead == NULL)
// return;
// 暴力检查
assert(pq->phead != NULL);
// 一个节点
// 多个节点
if (pq->phead->next == NULL)
{
free(pq->phead);
pq->phead = pq->ptail = NULL;
}
else
{
QNode* next = pq->phead->next;
free(pq->phead);
pq->phead = next;
}
pq->size--;
}
QDataType QueueFront(Queue* pq)
{
assert(pq);
// 暴力检查
assert(pq->phead != NULL);
return pq->phead->val;
}
QDataType QueueBack(Queue* pq)
{
assert(pq);
// 暴力检查
assert(pq->ptail != NULL);
return pq->ptail->val;
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->size == 0;
}
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
void TreeLevelOrder(BTNode* root)
{
// 创建队列结构体变量,用于存储二叉树节点指针
Queue q;
// 初始化队列(清空队列,设置头尾指针为NULL,大小为0)
QueueInit(&q);
// 若根节点存在,将其入队(作为遍历起点)
if (root)
QueuePush(&q, root);
// 当队列非空时,持续处理节点
while (!QueueEmpty(&q))
{
// 获取队头节点(当前待处理的节点)
BTNode* front = QueueFront(&q);
// 出队队头节点(移除队列头部,避免重复访问)
QueuePop(&q);
// 判断当前节点是否为空(处理NULL节点情况)
if (front)
{
// 打印非空节点的值(例如:1 2 3 ...)
printf("%d ", front->val);
// 将当前节点的左子节点入队(若为空则入队NULL,后续会被识别为"N")
QueuePush(&q, front->left);
// 将当前节点的右子节点入队(若为空则入队NULL,后续会被识别为"N")
QueuePush(&q, front->right);
}
else
{
// 当节点为NULL时,打印"N"表示该位置为空(例如:N N 4 ...)
// 这是为完整展示树结构(包括缺失子节点)而设计的处理
printf("N ");
}
}
// 遍历结束后打印换行符,确保输出格式整洁
printf("\n");
// 销毁队列,释放动态分配的内存(避免内存泄漏)
QueueDestroy(&q);
}
ai版本
// 队列节点定义
typedef struct QueueNode {
BTNode* data; // 存储指向二叉树节点的指针
struct QueueNode* next;
} QueueNode;
// 队列结构
typedef struct {
QueueNode* head;
QueueNode* tail;
int size;
} Queue;
// 队列初始化
void QueueInit(Queue* queue) {
queue->head = queue->tail = NULL;
queue->size = 0;
}
// 队列入队
void QueuePush(Queue* queue, BTNode* node) {
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
newnode->data = node;
newnode->next = NULL;
if (queue->head == NULL) {
queue->head = queue->tail = newnode;
} else {
queue->tail->next = newnode;
queue->tail = newnode;
}
queue->size++;
}
// 队列出队
void QueuePop(Queue* queue) {
if (queue->head == NULL) return;
QueueNode* temp = queue->head;
queue->head = queue->head->next;
if (queue->head == NULL) {
queue->tail = NULL;
}
free(temp);
queue->size--;
}
// 队列是否为空
int QueueEmpty(Queue* queue) {
return queue->head == NULL;
}
// 层序遍历
void LevelOrder(BTNode* root) {
if (root == NULL) return;
Queue queue;
QueueInit(&queue);
// 根节点入队
QueuePush(&queue, root);
while (!QueueEmpty(&queue)) {
// 出队
BTNode* front = queue.head->data;
QueuePop(&queue);
// 访问节点
printf("%d ", front->data);
// 左子树入队
if (front->left != NULL) {
QueuePush(&queue, front->left);
}
// 右子树入队
if (front->right != NULL) {
QueuePush(&queue, front->right);
}
}
}
层序遍历过程:
- 根节点1入队 → 出队1,访问1 → 2和4入队
- 出队2,访问2 → 3入队
- 出队4,访问4 → 5和6入队
- 出队3,访问3 → 无子节点
- 出队5,访问5 → 无子节点
- 出队6,访问6 → 无子节点
层序遍历结果:1 2 4 3 5 6
3.4 二叉树的其他常见操作
1. 计算二叉树节点总数
int TreeSize(BTNode* root) {
return root == NULL ? 0 :
TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 二叉树节点数量(递归实现)
int TreeSize(BTNode* root)
{
// 递归终止条件:空树返回0
if (root == NULL)
return 0;
// 递归计算:左子树节点数 + 右子树节点数 + 1(当前节点)
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
递归分析:
- 终止条件:空树返回0
- 递归关系:节点总数 = 左子树节点数 + 右子树节点数 + 1(当前节点)
- 优势:简洁、符合二叉树的递归定义
重要提示:不要使用静态变量实现TreeSize,因为这会导致多次调用结果错误(如第一次调用返回6,第二次调用返回12,第三次调用返回18)。
2. 计算二叉树高度
int TreeHeight(BTNode* root) {
if (root == NULL) {
return -1; // 空树高度为-1,使叶子节点高度为0,即第一层高为0,第二层高为1,如果把-1改为0,那是不是以第一层高为1
}
int left_height = TreeHeight(root->left);
int right_height = TreeHeight(root->right);
return (left_height > right_height ? left_height : right_height) + 1;
}
递归图如下:

高度定义:根节点到最远叶子节点的边数
- 叶子节点高度 = 0
- 单节点树高度 = 0
- 两层树高度 = 1
3. 查找第K层节点个数
思路:第k层的节点 = 左子树第k-1层的节点 + 右子树第k-1层的节点
int TreeKLevel(BTNode* root, int k) {
if (root == NULL || k <= 0) {
return 0;
}
if (k == 1) {
return 1; // 当前层,计数
}
// 递归计算左右子树第k-1层的节点数
return TreeKLevel(root->left, k-1) + TreeKLevel(root->right, k-1);
}
// 二叉树第k层节点数
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0); // 确保k至少为1
// 递归终止:空树或k=0时返回0
if (root == NULL)
return 0;
// 当前层为第1层(k=1)时,返回1
if (k == 1)
return 1;
// 递归计算:左子树第k-1层 + 右子树第k-1层
return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}
4. 查找节点(返回节点指针)
// 查找节点(返回节点指针)
BTNode* TreeFind(BTNode* root, int x)
{
if (root == NULL)
return NULL; // 未找到
// 当前节点匹配
if (root->val == x)
return root;
// 递归查找左子树
BTNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
// 递归查找右子树
BTNode* ret2 = TreeFind(root->right, x);
if (ret2)
return ret2;
return NULL; // 未找到
}
5.计算二叉树叶子节点个数
// 计算二叉树的叶子节点个数(叶子节点定义:左右子树均为空的节点)
int TreeLeafCount(BTNode* root)
{
// 边界条件1:空树处理(root为NULL)
// 说明:若当前子树为空,直接返回0(避免空指针解引用,确保递归安全)
if (root == NULL)
return 0;
// 边界条件2:叶子节点判定
// 说明:当前节点的左右子树均为空(left == NULL && right == NULL)时,该节点是叶子节点
// 返回1表示当前节点贡献1个叶子节点
if (root->left == NULL && root->right == NULL)
return 1;
// 递归核心逻辑
// 说明:整棵树的叶子节点数 = 左子树的叶子节点数 + 右子树的叶子节点数
// 递归调用原理:
// - 通过递归遍历左子树,统计左子树中的所有叶子节点
// - 通过递归遍历右子树,统计右子树中的所有叶子节点
// - 两者相加即为整棵树的叶子节点总数
return TreeLeafCount(root->left) + TreeLeafCount(root->right);
}
3.5 二叉树操作核心功能
1. 通过前序遍历字符串构建二叉树(如 “ABD##E#H##CF##G##”)
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// 二叉树节点结构
typedef struct TreeNode {
char val; // 节点存储的字符值
struct TreeNode* left; // 指向左子节点
struct TreeNode* right; // 指向右子节点
} TreeNode;
// 创建新节点
TreeNode* createNode(char val) {
// 为新节点分配内存
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
node->val = val; // 设置节点值
node->left = NULL; // 初始化左子节点为空
node->right = NULL; // 初始化右子节点为空
return node;
}
// 递归构建二叉树
TreeNode* buildTree(char* s, int* pos) {
// 关键点1:检查当前字符是否为空节点标记('#')
// 如果是空节点,直接返回NULL并移动指针
if (s[*pos] == '#') {
(*pos)++; // 移动字符串指针到下一个位置
return NULL;
}
// 关键点2:创建当前节点(非空节点)
TreeNode* root = createNode(s[*pos]);
(*pos)++; // 移动字符串指针到下一个位置
// 关键点3:递归构建左子树
// 前序遍历中,根节点后紧跟左子树
root->left = buildTree(s, pos);
// 关键点4:递归构建右子树
// 左子树构建完成后,紧跟右子树
root->right = buildTree(s, pos);
return root; // 返回构建完成的子树根节点
}
// 前序遍历打印二叉树(用于验证构建结果)
void preOrder(TreeNode* root) {
// 如果当前节点为空,打印空节点标记
if (root == NULL) {
printf("# "); // 使用#表示空节点
return;
}
// 前序遍历顺序:根 -> 左 -> 右
printf("%c ", root->val); // 访问根节点
preOrder(root->left); // 递归遍历左子树
preOrder(root->right); // 递归遍历右子树
}
// 释放二叉树内存(防止内存泄漏)
void freeTree(TreeNode* root) {
if (root == NULL) return; // 空节点无需释放
// 递归释放左右子树
freeTree(root->left); // 先释放左子树
freeTree(root->right); // 再释放右子树
free(root); // 最后释放当前节点
}
int main() {
// 前序遍历字符串表示(#表示空节点)
char s[] = "ABD#E#H##CF#G##"; // A B D # E # H # # C F # G # #
int pos = 0; // 当前处理字符串位置(从0开始)
TreeNode* root = buildTree(s, &pos); // 构建二叉树
// 验证:打印构建的二叉树前序遍历
printf("构建的二叉树前序遍历: ");
preOrder(root);
printf("\n");
// 释放内存
freeTree(root);
return 0;
}
2. 二叉树销毁(TreeDestroy)
// 二叉树销毁(后序遍历释放内存)
void TreeDestroy(BTNode* root)
{
// 安全检查:空树直接返回
if (root == NULL)
return;
// 递归销毁左右子树(后序遍历:先左后右再根)
TreeDestroy(root->left); // 销毁左子树
TreeDestroy(root->right); // 销毁右子树
free(root); // 释放当前节点内存
}
关键设计原理:
-
后序遍历的必要性:
- 释放顺序:
左子树 → 右子树 → 根节点 - 为什么不能先释放根?
如果先释放根,root->left和root->right指针变为悬挂指针,导致无法访问子树
- 释放顺序:
-
内存安全验证:
// 以树 A(1) -> B(2) -> C(3) 为例 TreeDestroy(1): TreeDestroy(2): TreeDestroy(3): // 先销毁叶子节点 free(3) free(2) free(1) -
与层序销毁的对比:
方法 空间复杂度 代码复杂度 内存安全 后序递归 O(h)(递归栈) 简单 ✅ 安全 层序遍历 O(n)(队列) 复杂 ⚠️ 需额外队列 -
调用后注意事项:
BTNode* root = CreateTree(); TreeDestroy(root); // 释放所有节点 root = NULL; // 避免悬挂指针
🔐 为什么必须置空?
C语言中指针不置空会导致悬挂指针(Dangling Pointer),可能引发段错误(Segmentation Fault)。
3. 判断完全二叉树(IsCompleteTree)
// 判断二叉树是否为完全二叉树
bool IsCompleteTree(BTNode* root)
{
// 空树是完全二叉树
if (root == NULL)
return true;
// 创建队列用于层序遍历
Queue q;
QueueInit(&q);
QueuePush(&q, root);
// 标志位:记录是否已遇到空节点
bool encounteredNull = false;
// 层序遍历
while (!QueueEmpty(&q))
{
BTNode* node = QueueFront(&q);
QueuePop(&q);
// 遇到空节点
if (node == NULL)
{
encounteredNull = true;
}
else
{
// 已遇到空节点但当前节点非空 → 非完全二叉树
if (encounteredNull)
return false;
// 将左右子节点入队(包括NULL)
QueuePush(&q, node->left);
QueuePush(&q, node->right);
}
}
return true;
}
核心原理(完全二叉树的判定标准):
完全二叉树的层序遍历中,一旦出现空节点,后面的所有节点必须为空
判定逻辑分步解析:
-
完全二叉树示例(有效):
层序遍历:[1,2,3,4,5,6] 队列过程: [1] → 1非空 → 入队[2,3] [2,3] → 2非空 → 入队[4,5] → [3,4,5] [3,4,5] → 3非空 → 入队[6] → [4,5,6] [4,5,6] → 4,5,6均非空 → 无空节点 → 返回true -
非完全二叉树示例(无效):
层序遍历:[1,2,3,4,5,7] // 6缺失 队列过程: [1] → 入队[2,3] [2,3] → 2入队[4,5], 3入队[NULL,7] → [4,5,NULL,7] [4,5,NULL,7] → 4→入队[NULL,NULL] → [5,NULL,7,NULL,NULL] 5→入队[NULL,NULL] → [NULL,7,NULL,NULL,NULL,NULL] NULL → encounteredNull=true 7→非空且encounteredNull=true → return false -
关键标志位
encounteredNull的作用:- 一旦遇到
NULL,设置encounteredNull=true - 后续所有节点必须为
NULL(否则返回false)
- 一旦遇到
为什么层序遍历是唯一可靠方法?
| 遍历方式 | 能否判断完全二叉树 | 原因 |
|---|---|---|
| 前序/中序/后序 | ❌ 不能 | 无法保证层次顺序 |
| 层序遍历 | ✅ 能 | 直接验证"空节点后无非空节点"的特性 |
📌 完全二叉树的严格定义:
深度为k的二叉树,若第k层节点都集中在左侧,则为完全二叉树。
(即:层序遍历中,所有非空节点在空节点之前)
3.6 递归实现的关键点
1. 递归终止条件
- 对于遍历:当节点为NULL时
- 对于其他操作:根据具体问题确定终止条件
2. 递归调用
- 将问题分解为子问题(左子树、右子树)
- 递归调用自身处理子问题
3. 递归与分治思想
- 递归是分治思想的体现:将大问题分解为小问题
- 二叉树的递归实现比迭代实现更简洁,因为二叉树的结构本身就是递归的
完整代码
// 二叉树节点结构体定义
typedef struct BinTreeNode
{
struct BinTreeNode* left; // 指向左子节点的指针
struct BinTreeNode* right; // 指向右子节点的指针
int val; // 节点存储的整数值
}BTNode;
// 创建新节点的函数
BTNode* BuyBTNode(int val)
{
// 分配内存空间,大小为BTNode结构体的大小
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
// 内存分配失败检查
if (newnode == NULL)
{
perror("malloc fail"); // 输出错误信息
return NULL; // 返回NULL表示创建失败
}
// 初始化节点值和指针
newnode->val = val; // 设置节点值
newnode->left = NULL; // 左子节点初始化为空
newnode->right = NULL; // 右子节点初始化为空
return newnode; // 返回新创建的节点
}
// 手动构建一棵示例二叉树
BTNode* CreateTree()
{
// 创建各个节点(值分别为1-6)
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
// 构建树的结构(根节点1,左子树2,右子树4)
n1->left = n2; // 节点1的左子节点指向节点2
n1->right = n4; // 节点1的右子节点指向节点4
n2->left = n3; // 节点2的左子节点指向节点3
n4->left = n5; // 节点4的左子节点指向节点5
n4->right = n6; // 节点4的右子节点指向节点6
return n1; // 返回根节点
}
// 前序遍历:根->左->右
void PreOrder(BTNode* root)
{
// 递归终止条件:当前节点为空
if (root == NULL)
{
printf("N "); // 空节点用"N"表示
return;
}
// 访问根节点
printf("%d ", root->val); // 先打印当前节点值
// 递归遍历左子树
PreOrder(root->left);
// 递归遍历右子树
PreOrder(root->right);
}
// 中序遍历:左->根->右
void InOrder(BTNode* root)
{
// 递归终止条件
if (root == NULL)
{
printf("N ");
return;
}
// 递归遍历左子树
InOrder(root->left);
// 访问根节点
printf("%d ", root->val);
// 递归遍历右子树
InOrder(root->right);
}
// 后序遍历(函数声明提前,因为后面会调用)
void PostOrder(BTNode* root);
// 递归计算二叉树节点总数(正确实现)
int TreeSize(BTNode* root)
{
// 递归终止条件:空节点返回0
// 递归公式:节点总数 = 左子树节点数 + 右子树节点数 + 1(当前节点)
return root == NULL ? 0 :
TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 递归计算二叉树高度(高度定义:根节点到最远叶子节点的边数)
int TreeHeight(BTNode* root)
{
// 递归终止条件:空节点高度为-1(这样叶子节点高度为0)
if (root == NULL)
return -1;
// 计算左右子树高度
int left_height = TreeHeight(root->left);
int right_height = TreeHeight(root->right);
// 当前节点高度 = 左右子树高度的最大值 + 1
return (left_height > right_height ? left_height : right_height) + 1;
}
// 主函数
int main()
{
BTNode* root = CreateTree(); // 构建示例树
// 前序遍历示例:1 2 3 4 5 6
printf("前序遍历: ");
PreOrder(root);
printf("\n");
// 中序遍历示例:3 2 1 5 4 6
printf("中序遍历: ");
InOrder(root);
printf("\n");
// 测试TreeSize函数(正确实现)
// 递归实现:避免使用静态变量(线程不安全)或指针参数(调用复杂)
printf("节点总数: %d\n", TreeSize(root)); // 输出6
// 验证TreeSize的多次调用(确保无副作用)
printf("多次调用结果: %d %d %d\n",
TreeSize(root), TreeSize(root), TreeSize(root));
// 输出: 6 6 6(证明函数是纯函数,无状态依赖)
return 0;
}
3.6 实际应用与总结
1. 二叉树遍历的应用场景
- 表达式求值:中序遍历得到中缀表达式,前序/后序遍历得到前缀/后缀表达式
- 二叉搜索树:中序遍历得到有序序列
- 哈夫曼编码:通过遍历哈夫曼树生成编码
- 数据压缩:哈夫曼树的遍历用于生成压缩编码
2. 二叉树链式结构的优势
- 内存效率:只分配需要的节点,节省空间
- 灵活性:可以轻松构建任意形状的二叉树
- 适用性:适用于各种二叉树操作,如遍历、查找、插入、删除等





















 1964
1964

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








