首先上动态规划的文章然后直接上题
目录
第一道题:
P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
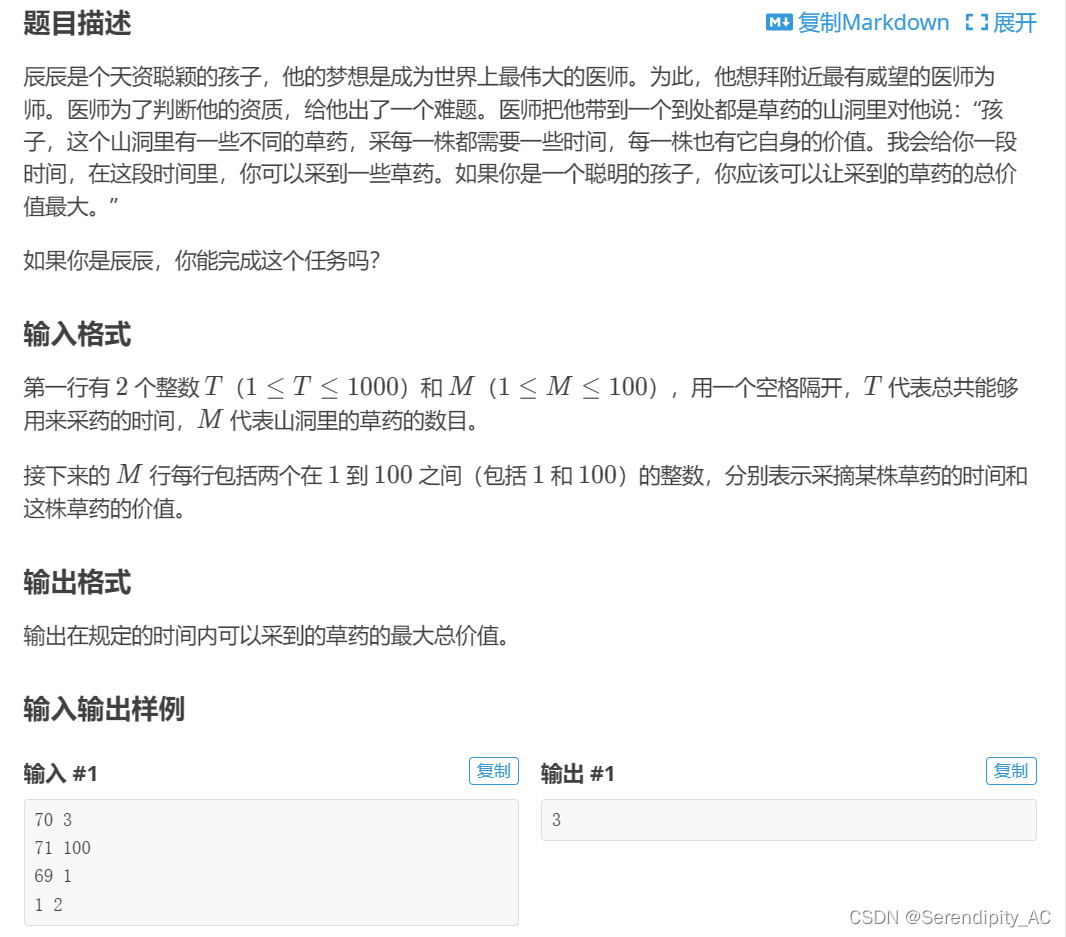
思路:
这个其实是一个很基础的01背包问题,没有什么难度,就是注意和完全背包区别,假如用滚动数组优化的话,01背包是从大到小遍历,而完全背包则相反从小到大进行遍历,这里就不进行证明了
代码:
#include<bits/stdc++.h>
using namespace std;
int T; int M;
int t[105], w[105];
int f[1005];//表示在某个体积下可有的最大价值
int main() {
cin >> T >> M;
for (int i = 1; i <= M; i++) {
cin >> t[i] >> w[i];
}
for (int i = 1; i <= M; i++) {
for (int j = T; j >= t[i]; j--) {
f[j] = max(f[j], f[j - t[i]] + w[i]);
}
}
cout << f[T] << endl;
return 0;
}第二道题:
B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
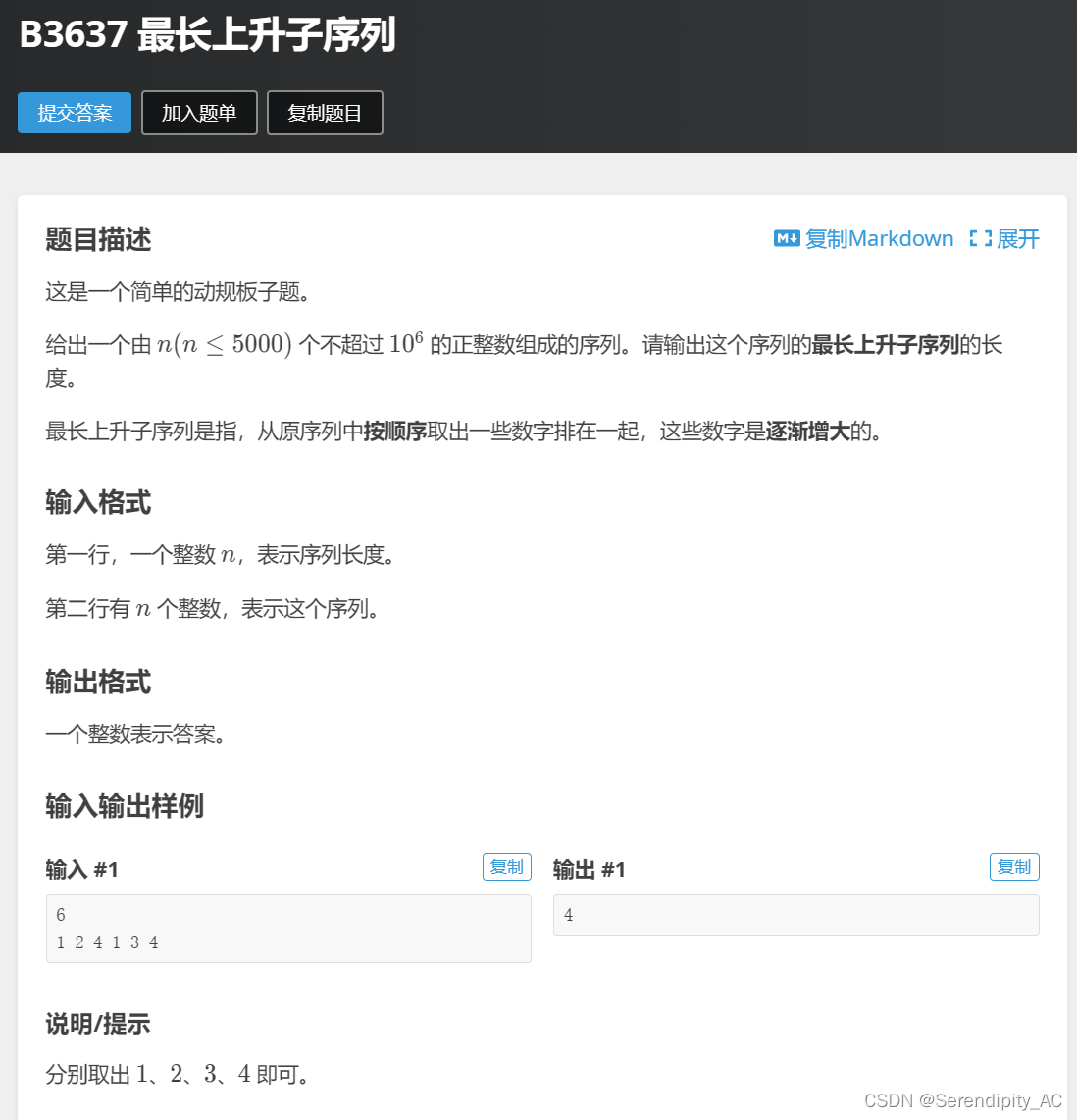
思路:
1.传统方法:用f[i]来表示在从第一个数字到第i个数字时能取到的最长的上升子序列,这时候很容易写出状态转移方程,当从前往后遍历到i的时候,如果有a[i]>a[j],则这时候可以选择选或者不选,而选或者不选取决于f[i]和f[j]+1的大小关系,则很容易知道状态转移方程为f[i]=max(f[i],f[j]+1),而答案则为f[i]中的最大值
2.STL(lower_bound)
这里只提供代码,不给出证明,有兴趣的可以自己去查
代码:
//传统
#include<bits/stdc++.h>
using namespace std;
int a[1005];
int f[1005];
int main() {
int n=5;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
f[0] = 1;
int ans = 0;
for (int i = 1; i < n; i++) {
f[i] = 1;
for (int j = 0; j < i; j++) {
if (a[i] > a[j])f[i] = max(f[i], f[j] + 1);
}
if (ans < f[i])ans = f[i];
}
cout << ans << endl;
return 0;
}//STL
#include<bits/stdc++.h>
using namespace std;
int a[5005],ans[5005];
int main() {
int n; cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
int L1 = 1; ans[L1] = a[1];
for (int i = 2; i <= n; i++) {
if (a[i] > ans[L1])ans[++L1] = a[i];
else *lower_bound(ans + 1, ans + 1 + L1, a[i]) = a[i];
}
cout << L1 << endl;
return 0;
}注:
有关lower_bound的解法可以去看看这道题P1020 [NOIP1999 普及组] 导弹拦截 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
附上本人AC代码:
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000010
int a[maxn], L_1[maxn],L_2[maxn];
int main() {
int cnt = 1;
while (cin>>a[cnt])
{
cnt++;
}
cnt--;
int L1 = 1,L2=1;
L_1[L1] = a[1];
L_2[L2] = a[1];
for (int i = 2; i <= cnt; i++) {
if (L_1[L1] >= a[i])L_1[++L1] = a[i];
else *upper_bound(L_1 + 1, L_1 + 1 + L1, a[i], greater<int>())=a[i];//把第一个小于a[i]的换掉,求最大不上升子序列
if (L_2[L2] < a[i])L_2[++L2] = a[i];
else *lower_bound(L_2 + 1, L_2 + 1 + L2, a[i]) = a[i];//把第一个大于a[i]的换掉,求最大上升子序列=最少的不上升子序列的个数
}
cout << L1 << endl << L2 << endl;
return 0;
}第三道题:
B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
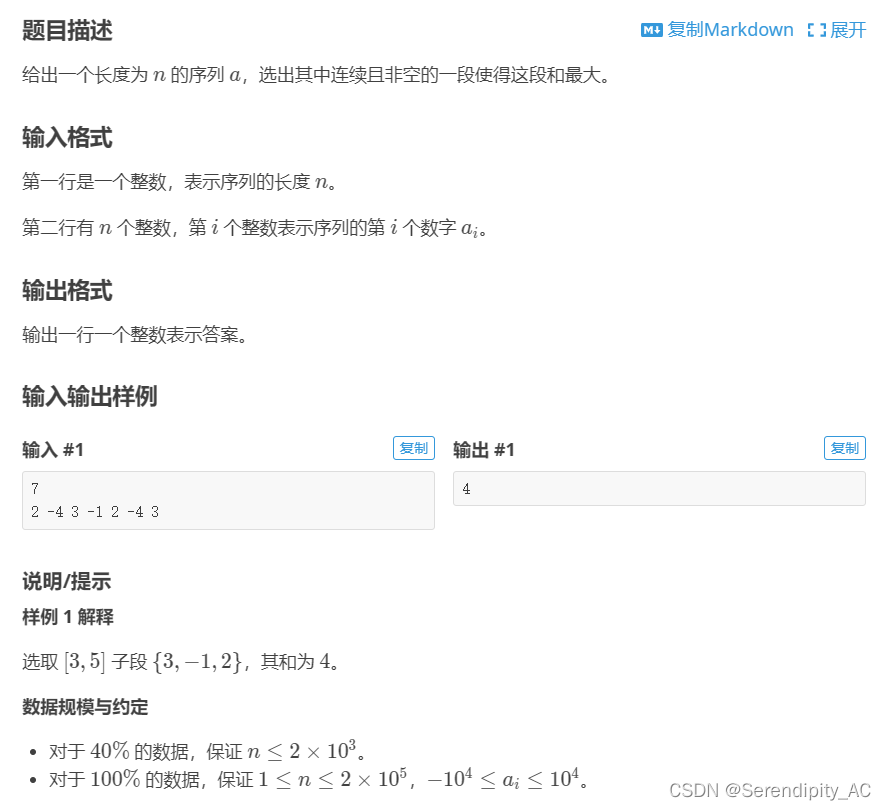
思路:
这道题就更加的简单了,只给出状态转移方程:ans[i] = max(ans[i] + ans[i - 1], ans[i]);
代码:
#include<bits/stdc++.h>
using namespace std;
int a[200500], ans[200500];
int main() {
int n; cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
ans[1] = a[1];
for (int i = 2; i <= n; i++) {
ans[i] = a[i];
ans[i] = max(ans[i] + ans[i - 1], ans[i]);
}
sort(ans + 1, ans + 1 + n);
cout << ans[n] << endl;
return 0;
}第四道题:
LCS - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路:
这题其实就是在求最大公共子序列,同时我们知道求最大公共子序列个数很好求仅需要这一段代码
s1 = '0', s2 = '0';
cin >> a >> b;
s1 += a, s2 += b;//初始化小细节这样可以减少后面的判断
for (int i = 1; i <= s1.length() - 1; i++) {
for (int j = 1; j <= s2.length() - 1; j++) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);//假设一开始s1[i]!=s2[j]给f[i][j]赋初值
if (s1[i] == s2[j])f[i][j] = max(f[i - 1][j - 1] + 1, f[i][j]);
}
}主要是理解f[i][j]为s1中第i个前和s2中第j个前俩最长公共子序列,再结合这个图理解一下就好了
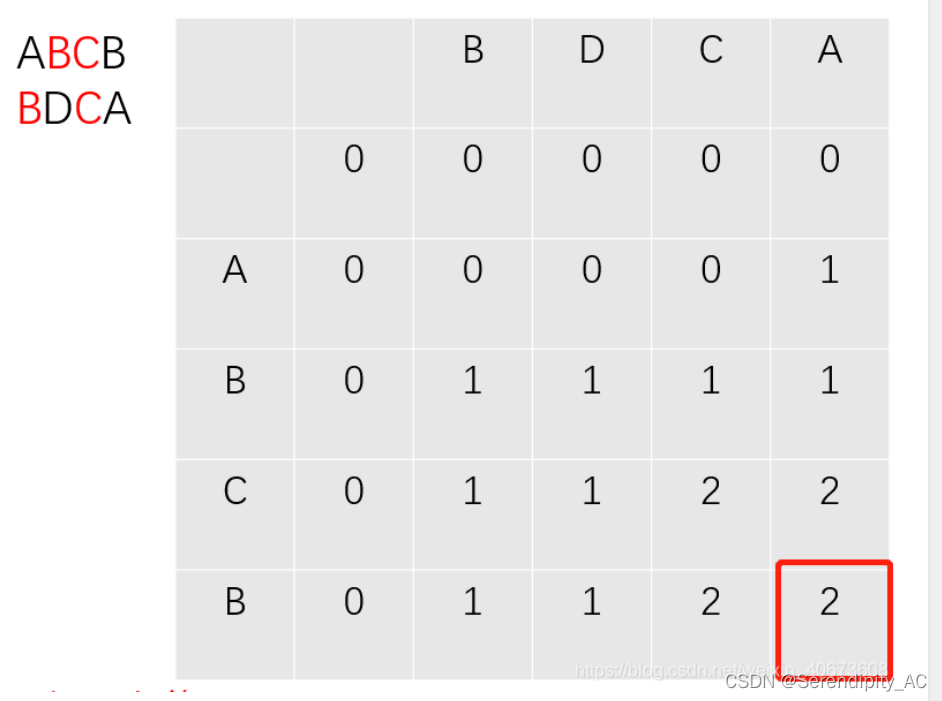
然后至于怎么把他输出出来呢,我们可以采用回溯的方法,代码如下
int i = s1.length() - 1, j = s2.length() - 1;
while (f[i][j] > 0)
{
if (s1[i] == s2[j]) {//如果俩相同最长公共子序列中肯定有该字母
ans[f[i][j]] = s1[i];
i--, j--;//回溯
}
else {
if (f[i][j] == f[i][j - 1])j--;//如果是和f[i][j-1]则证明是f[i][j-1]>f[i-1][j]则后面f[i][j]== f[i][j - 1],则回溯时j--
else i--;//同理
}
}代码:
#include<bits/stdc++.h>
using namespace std;
int f[3005][3005];
char ans[3005];
string s1, s2,a,b;
int main(){
s1 = '0', s2 = '0';
cin >> a >> b;
s1 += a, s2 += b;
for (int i = 1; i <= s1.length()-1; i++) {
for (int j = 1; j <= s2.length()-1; j++) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (s1[i] == s2[j])f[i][j] = max(f[i - 1][j - 1]+1, f[i][j]);
}
}
//cout << s1 << endl << s2 << endl;
int i = s1.length()-1, j = s2.length()-1;
while (f[i][j]>0)
{
if (s1[i] == s2[j]) {
ans[f[i][j]] = s1[i];
i--, j--;
}
else {
if (f[i][j] == f[i][j - 1])j--;
else i--;
}
}
cout << ans + 1 << endl;
return 0;
}





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








