信奥一本通1314：【例3.6】过河卒(Noip2002)

最新推荐文章于 2024-09-10 06:22:18 发布

原创最新推荐文章于 2024-09-10 06:22:18 发布 · 1k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#1024程序员节 #c++

算法专栏收录该内容

2 篇文章

订阅专栏

这是一篇关于解决棋盘上卒从A点到B点路径计数问题的博客，利用递推算法而非搜索。题目中卒只能向下或向右移动，而马的控制点不可穿越。输入为棋盘大小和马的位置，输出为到达B点的路径数。博主通过建立二维数组存储棋盘信息，并用递推方法计算路径，最终输出路径总数。

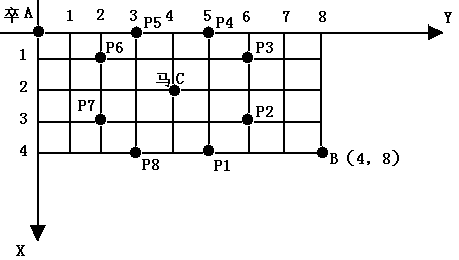
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

【输入】

给出n、m和C点的坐标。

【输出】

从A点能够到达B点的路径的条数。

【输入样例】

8 6 0 4

【输出样例】

这道题一眼看过去想到的是用搜索来做，深搜或者广搜来找路径到达B点，然后记下此路径反复的搜索就可以计算出路径的条数。但是这题放在了“递推”的模块里，还是要用递推的方法去做。

我首先是用一个数组将棋盘的信息存下来，然后打表用来后面判断棋子能走的方向和马能控制到的地方。将棋盘的信息完善之后就可以循环递推求路径的条数啦。

AC源码

#include <bits/stdc++.h>
using namespace std;
int n,m,x,y;
int a[25][25];
int next1[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int next2[8][2]={{-2,-1},{-1,-2},{1,-2},{2,-1},{2,1},{1,2},{-1,2},{-2,1}};
long long f[25][25];
int main()
{
	cin>>n>>m>>x>>y;
	a[x][y] = 1;
	for(int i=0;i<8;i++){
		int tx = x+next2[i][0];
		int ty = y+next2[i][1];
		if(tx>=0&&tx<=n&&ty>=0&&ty<=m){
			a[tx][ty] = 1;
		}
	}
	f[0][0] = 1;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){
			for(int k=0;k<4;k++){
				int tx = i+next1[k][0];
				int ty = j+next1[k][1];
				if(tx>=0&&tx<=n&&ty>=0&&ty<=m){
					if(a[tx][ty]==0){
						f[i][j] = f[i][j]+f[tx][ty];
					}
				}
		    }
		}
	}
	printf("%lld",f[n][m]);
	return 0;
}