Barycentric Coordinates

https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-rendering-a-triangle/barycentric-coordinates

barycentric coordinates are particularly important in CG. they have a few functions and are the key to the next ray-triangle intersection algorithm proposed by Moller Trumbore that will be studied in the next chapter. how barycentric coordinates can be used in CG will be discussed at the end of this chapter.

barycentric coordinates can be used to express the position of any point located on the triangle with three scalars. the loation of this point includes any position inside the triangle, any position on any of the three edges of the triangles, or any one of the three triangle’s vertices themselves. to compute the position of this point using barycentric coordinates we use the following equation (1):

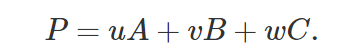
where A B and C are the vertices of a triangle and uu, vv, and ww (the barycentric coordinates), three real numbers (scalars) such that u+v+w=1u+v+w=1 (barycentric coordinates are normalized). Note that from two of the coordinates we can find the third one: w=1−u−vw=1−u−v from which we can establish that u+v≤1u+v≤1 (we will use this simple but important property later on). Equation 1 defines the position of a point P on the plane of the triangle formed by the vertices A, B and C. The point is within the triangle (A, B, C) if 0≤u,v,w≤10≤u,v,w≤1. If any one of the coordinates is less than zero or greater than one, the point is outside the triangle. If any of them is zero, P is on one of the lines joining the vertices of the triangle.

You can also simply use two coordinates (let’s say u and v) to express the coordinates of P in a two dimensional coordinate system defined by its origin (A) and the edge AB and AC (pretty much like expressing 2D points in the orthogonal two-dimensional coordinate system defined by an x- and y-axis. The only difference in our case is that AB and AC are not necessarily orthogonal and that the origin of this coordinate system is A). Anyway, just to say that you can define a position inside the triangle with the equation P=A+u∗AB+v∗ACP=A+u∗AB+v∗AC (where u≥0u≥0 and v≥0v≥0 and u+v≤1u+v≤1). This equation can read as, “starts from A, move a little bit in the direction of AB, then a little bit in the direction of AC and you will find P”. Now if you develop this equation you can write:

P=A+u(B−A)+v(C−A)=A+uB−uA+vC−vA=(1−u−v)∗A+u∗B+v∗C

This equation is similar to equation 1 except that if w=1−u−v you have the following formula:
P=w∗A+u∗B+v∗C
instead of
P=u∗A+v∗B+w∗C.
These two equations are perfectly similar but it’s hard to understand why we usually write (1−u−v)∗A+u∗B+v∗C instead of u∗A+v∗B+(1−u−v)∗C without the above explanation.
两种写法都是可以的，但是通常使用第一种写法。

barycentric coordinnates are also known as areal coordinates 面积坐标. although not very commonly used, this term indicates that the coordinates u, v and w are proportional to the area of the three sub-triangles defined by P, the point located on the triangle, and the triangle’s vertices (A, B, C). These three sub-triangles are denoted ABP, BCP, CAP (see figure 1).

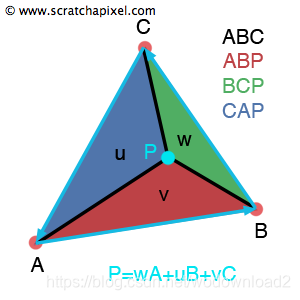
Figure 1: barycentric coordinates can be seen as the area of sub-triangles CAP (for u), ABP (for v) and BCP (for w) over the area of the triangle ABC which is why the are also called areal coordinates.

Which leads us to the formulas used to compute the barycentric coordinates:

In the rest of the lesson we will assume that u makes us move along the edge AB (if u=1 then P=B) and v along the edge AC (if v=1 then P=C). Which is the reason why we will use the area of the sub-triangle CAP to compute u and the area of the sub-triangle ABP to compute v. This is a convention that most people follow in the CG programming community (when we will learn how to use barycentric coordinates to interpolate vertex data you will have a visual example (figure 3) to better understand this).

Now computing the area of a triangle is trivial. If you duplicate the triangle and mirror it along its longest edge, you get a parallelogram. To compute the area of a parallelogram, simply compute its base, its side and multiply these two numbers together scaled by sin(θθ), where θθ is the angle subtended by the vectors AB and AC (figure 2). To create the parallelogram we used two triangles, therefore the area of one triangle is half the area of the parallelogram.

With this in hands, it becomes easy to compute u and v (w is computed out of u and v as explained before).

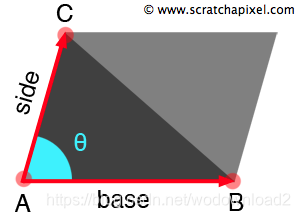
Figure 2: to compute the area of a triangle we start from the formula used to compute a parallelogram (its base multiplied by its height H). To compute H, we multiply sin(θθ) by the length of the vector AC.

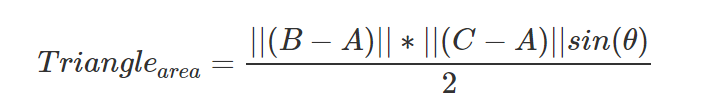
To make things easier, we can take advantage of the fact that the area of the sub-triangles ABP, BCP and CAP are proportional to the lengths of the cross product that we computed in the previous chapter to find P, the intersection point. This is one of the cross product properties: the magnitude of the cross product can be interpreted as the area of the parallelogram. Therefore we don’t need to explicitly compute the previous formula (which includes an “expansive” sin(θ). We can simply use instead:

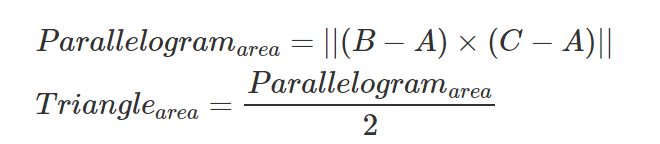
Note than in mathematical terms, the double bars notation (|| ||) means “length of” (lesson 4). In other words we need to compute the length of the vector resulting of the cross product (C-B)x(P-B). We know how to compute the cross product of two vectors and the length of a vector so we have now all we need to compute the barycentric coordinates of the intersection point:

bool rayTriangleIntersect( 
    const Vec3f &orig, const Vec3f &dir, 
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2, 
    float &t, float &u, float &v) 
{ 
    // compute plane's normal
    Vec3f v0v1 = v1 - v0; 
    Vec3f v0v2 = v2 - v0; 
    // no need to normalize
    Vec3f N = v0v1.crossProduct(v0v2); // N 
    float area = N.length() / 2; // area of the triangle 
 
    ... 
 
    // Step 2: inside-outside test
    Vec3f C; // vector perpendicular to triangle's plane 
 
    // edge 0
    ... 
 
    // edge 1
    Vec3f edge1 = v2 - v1; 
    Vec3f vp1 = P - v1; 
    C = edge1.crossProduct(vp1); 
    u = (C.length() / 2) / area; 
    if (N.dotProduct(C) < 0)  return false; // P is on the right side 
 
    // edge 2
    Vec3f edge2 = v0 - v2; 
    Vec3f vp2 = P - v2; 
    C = edge2.crossProduct(vp2); 
    v = (C.length() / 2) / area; 
    if (N.dotProduct(C) < 0) return false; // P is on the right side; 
 
    return true; // this ray hits the triangle 
} 

The plane normal should not be normalized because we use the length of the vector to compute the triangle area.