一、题目描述
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-size-subarray-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
二、思考

核心思路->我们可以利用滑动窗口思想通过移动左右指针来获取到局部最优解
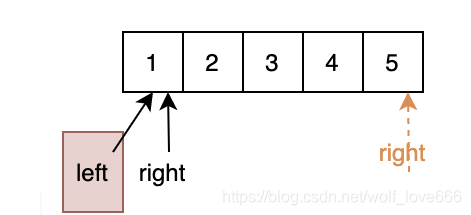
固定左指针,不断移动右指针,如果左指针和右指针之间的数值累计和大于等于 target 目标值,我们则暂停,跳到情况二。
比如上图中黄色右指针移动到 5 的时候,已经符合大于等于 target 目标值。则暂停右指针,进入情况二中。
//固定左指针,移动右指针,如果和小于目标值
if (right < nums.length && sums < target){
sums = sums+nums[right];
right++;
}
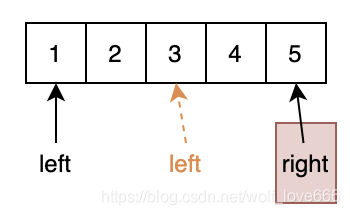
固定右指针 right,不断移动左指针,如果移动左指针的时候,左指针到右指针之间数值累计和小于 target 目标值,则暂停,跳到情况一继续。
比如我们上述移动左指针到 3 的时候,黄色指针 left 的地址,发现继续移动 left 指针已经不满了,则暂停
else{
//固定右指针,移动左指针,如果当前总和值和目标值相等,则记录下
if (sums >= target && (finalLeft == -1 || finalRight-finalLeft > right -left )){
finalLeft=left;
finalRight=right;
}
sums = sums - nums[left];
left++;
}
三、代码
3.1、是我为了大家好理解写的代码,只有一个 while 循环那么直接一眼可以看出来就是 O(n)。
public static int minSubArrayLen(int target, int[] nums) {
//1-条件控制
if (nums.length < 1){
return 0;
}
//利用双指针遍历数组
int left =0,right=0,finalLeft=-1,finalRight=-1;
int sums = 0;
while (left < nums.length){
//固定左指针,移动右指针,如果和小于目标值
if (right < nums.length && sums < target){
sums = sums+nums[right];
right++;
}else{
//固定右指针,移动左指针,如果当前总和值和目标值相等,则记录下
if (sums >= target && (finalLeft == -1 || finalRight-finalLeft > right -left )){
finalLeft=left;
finalRight=right;
}
sums = sums - nums[left];
left++;
}
}
if (finalLeft !=-1){
return finalRight-finalLeft;
}
return 0;
}
3.2、根据所有的面试官来考虑的话 其实代码越少,越简单,反而会增加好感,所以代码进行下优化。这里面你看到的是两个 while,但是你仔细分析下时间复杂度实际上是与 3.1 相同,只是一个变形体
public static int minSubArrayLen2(int target, int[] nums) {
//初始化数组长度
int n = nums.length;
//初始化左右指针
int left = 0, right = 0;
//初始化滑动窗口局部最优解
int MinLength = Integer.MAX_VALUE;
//初始化临时求和变量
int sum = 0;
//固定左指针,移动右指针
while (right < n) {
//添加元素到临时求和变量
sum += nums[right];
//如果临时变量求和不满足目标值说明我们不需要考虑,所以继续移动右指针,如果我们的临时变量求和满足了目标值,就需要移动左指针。
while (sum >= target) {
//比较当前滑动窗口大小,取滑动窗口最小的值
MinLength = Math.min(MinLength, right - left + 1);
//减少当前移动的左指针的值
sum -= nums[left];
//左指针继续移动
left++;
}
//继续移动右指针
right++;
}
return MinLength == Integer.MAX_VALUE ? 0 : MinLength;
}
四、小结
题目中的进阶是算法时间复杂度为 O(nlogn),其实是需要用快排,那么为什么会有这样的问题呢?是因为我们在工作中,不可能只是单纯的记录下当时的答案,而是需要知道为什么,什么时候适合什么样的算法。我觉得这个可能是题目背后的意思吧。























 494
494











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










