力引导算法深入理解及其在d3.js中实现的源码分析

    中学时最喜欢的学科是物理，大学误打误撞读了计算机。最近在做图计算的相关工作，图的可视化中有一个非常重要的算法：“力引导算法”，这个算法的原理居然就是最简单的粒子间的作用力，真是没想到我喜爱的两个东西在这里结合起来了，也有一个感慨：虽然我们的抽象理论已经这么发达的今天，仍然还是需要这种模拟物理世界的“蛮力”算法。

    进入正题，我将按如下顺序带着疑问的由浅入深的讲解一下力引导算法（force-directed），作为自己工作的总结，如果有幸帮助到别人就完美了。

• 力引导算法解决了什么问题？
• 力引导算法的原理是什么？
• 力引导算法有哪里优点及缺点？
• 力引导算法在d3.js中怎么用？
• 力引导算法在d3.js是怎么实现的？

力引导算法解决了什么问题？

一句话：它很大程度上解决了非常困难的图的布局问题，看下面两张图，你觉得哪一张更清晰，实际上它们是一样的图

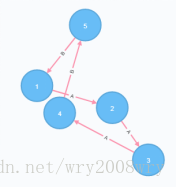
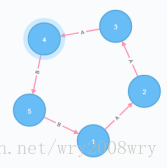
是不是第2张图看起来舒服多了，没有那么纠结。

图2的可视化更能展示出了这个图的本质：它是一个环形图。

通常我们通常可以通过以下标准来衡量一个图布局算法的好坏：
1 交叉的边要尽量少
2 边长要尽量均衡
3 布局要尽量对称
4 单位面积能放尽量多的结点
以上标准前面的更重要，而且基本上是满足一些就会减弱另一些，而力引导算法基本上能很好的平衡，所以它算是一个很好的图布局算法。

关于边的交叉，这里不得不提到图论中的一个概念：平面图，所谓平面图就是将一个图画出来，里面没有相交的边，这个过程叫做平面化。需要注意的是不是所有的图都可以平面化的，详情见这里：平面图。

力引导算法的原理是什么？

狭义的、一句话说就是：把相连的结点接到一起，并可能把不相连的节点推开。
再详细一点的解释：
图中的结点存在着两种力
相连的结点间存在引力（弹簧），其值通过胡克定律算出
结点相互之前存在着静电斥力，通过库仑定律处出
这两种力合成转化成位移，导致结点位移，反复迭代最终整个系统会稳定下来，达到某个阈值停止。


所以一般的实现步骤是：
1 初始化结点位置；
2 计算结点的各种受力；
3 计算合力并将其转化为位置；

4 反复迭代直到达到平衡状态；

力引导算法有哪里优点及缺点？

优点：
高质量
生成的布局交叉结点少、结点、边分布均匀、高对称性；
可扩展性
可以在其基础上进行扩展，比如固定某些点、让某些点只能在一个固定的轨迹上运动（比如固定其y轴或是让其在一个圆环轨道上运行）；
简单
由于其原理简单，实现起来也很容易；
交互性
由于算法本身是一个迭代的过程，布局生成是一个连续的过程，可以将这个过程可视化出来，非常直观。对于已经稳定的布局甚至可以手动手动某个点，然后算法重要布局，再次形成新的布局；
坚实的理论基础
其理论基础为物理定律，可以利用很多现成的方法；


缺点
时间复杂度高
由于使用多次迭代，而且单次迭代中需要计算每个点受到其它所有点的合力，所以基本上时间复杂度为O(n^3)；
会出现局部最优
由于初始布局的不同，最终生成的布局可以会陷入局部能量最小，可能与全局最小能量相差很远；

总体来说，力引导算法解决了其它算法很难解决的问题，目前仍然是最好的图布局算法

力引导算法在d3.js中怎么用？

Show me the code！下面是使用的源码，使用d3.js实现了一个力引导布局，你可以直接将上面的代码复制并保存为一个html文件中，直接点击打开，然后修改修改其中的参数看看效果，大胆尝试吧！

<style>
.links line {
  stroke: #999;
  stroke-opacity: 0.6;
}

.nodes circle {
  stroke: black	;
  stroke-width: 0px;
}
</style>

<!--用于显示图的窗口元素-->
<svg width="1400" height="600"></svg>

<script src="d3.v4.js"></script>
<script>

///创建界面
var svg = d3.select("svg");
var width = +svg.attr("width");
var height = +svg.attr("height");

var nodes_data =  [
    {"name": "1", "sex": "F"},
    {"name": "2", "sex": "F"},
    {"name": "3", "sex": "F"},
    {"name": "4", "sex": "F"},
    {"name": "5", "sex": "F"},
    {"name": "6", "sex": "F"},
    {"name": "7", "sex": "F"},
    {"name": "8", "sex": "F"},
    {"name": "9", "sex": "F"},
    {"name": "10", "sex": "F"},
    {"name": "11", "sex": "F"},
    ];

var links_data = [
    {"source": "1", "target": "2", "type":"A" },
    {"source": "1", "target": "3", "type":"A" },
    {"source": "1", "target": "4", "type":"A" },
    {"source": "2", "target": "5", "type":"A" },
    {"source": "3", "target": "5", "type":"A" },
    {"source": "4", "target": "5", "type":"A" },
    {"source": "4", "target": "6", "type":"A" },
    {"source": "5", "target": "7", "type":"A" },
    {"source": "5", "target": "8", "type":"A" },
    {"source": "5", "target": "9", "type":"A" },
    {"source": "6", "target": "10", "type":"A" },
    {"source": "7", "target": "11", "type":"A" },
    {"source": "8", "target": "11", "type":"A" },
    {"source": "9", "target": "11", "type":"A" },
    {"source": "10", "target": "11", "type":"A" }
];

//创建一个模拟器对象
var simulation = d3.forceSimulation().nodes(nodes_data);

///定义各种力
var link_force =  d3.forceLink(links_data).strength(1).id(function(d){return d.name;});  ///<连线间的引力
var charge_force = d3.forceManyBody().strength(-20000);    ///<斥力
var center_force = d3.forceCenter(width/2, height/2); ///<中心力
var radial_force = d3.forceRadial(200, width/2, height/2).strength(5); ///<分布在环上的力
var x_force =  d3.forceX(100).strength(1); ///<X轴力
var collide_force = d3.forceCollide(100).strength(1); ///<碰撞力

///将力应用到模拟器
simulation.force("charge_force", charge_force).force("radial_force", radial_force).force("links",link_force);

///tick事件
simulation.on("tick", tickActions);


var link = svg.append("g")
      .attr("class", "links")
    .selectAll("line")
    .data(links_data)
    .enter().append("line")
      .attr("stroke-width", 2)
   ;        

///界面上绘制结点
var node = svg.append("g")
        .attr("class", "nodes")
        .selectAll("circle")
        .data(nodes_data)
        .enter()
        .append("circle")
        .attr("r", 15)
        ;

///处理拖动
var drag_handler = d3.drag()
	.on("start", drag_start)
	.on("drag", drag_drag)
	.on("end", drag_end);	
	
drag_handler(node)

function drag_start(d) {
 if (!d3.event.active) simulation.alphaTarget(0.3).restart();
    d.fx = d.x;
    d.fy = d.y;
}

function drag_drag(d) {
  d.fx = d3.event.x;
  d.fy = d3.event.y;
}


function drag_end(d) {
  if (!d3.event.active) simulation.alphaTarget(0);
  d.fx = null;
  d.fy = null;
}
    
///响应tick事件，更新界面
function tickActions() {
      node.attr("cx", function(d) {
        return d.x;
      }).attr("cy", function(d) {
        return d.y;
      });
        
    link.attr("x1", function(d) { return d.source.x; })
    .attr("y1", function(d) { return d.source.y; })
    .attr("x2", function(d) { return d.target.x; })
    .attr("y2", function(d) { return d.target.y; });
}
</script>

上面的代码主要包含：
1 创建一个svg元素作为显示的容器；
2 定义了结点及连接边的数据；
3 实例化一个力布局模拟器，使用结点信息初始化；
4 创建各种力，施加于模拟器；
5 创建结点及连线的界面元素；
6 处理结点的拖动，将界面的动作反向作用到模拟器内部数据；

7 处理模拟器的tick事件，将模拟器内部的数据可视化出来，每一次tick代表一帧将其反应到界面上；

力引导算法在d3.js到底是怎么实现的？

上面的们提到力引导算法的一般化实现流程为：
1 初始化结点位置
2 计算结点的各种受力
3 计算合力并将其转化为位置
4 反复迭代直到达到平衡状态
在d3.js中也是如此，只是一般的框架为了扩展性，会有一些特别的东西在里面，下面我们来看看d3.js中是怎么实现的。d3.js force的源代码在这里：https://github.com/d3/d3-force/tree/master/src
模块划分如下：
center.js - “中心力”实现，实现结点向中心点收拢；
collide.js - 处理结点的碰撞，即结点在指定半径内不相碰，使用四叉树实现；
constant.js - 定义常量用的函数，因为d3.js中均是使用函数的方式取值，如果是一个常数需要将其包装成一个函数；
jiggle.js - 结点随机抖动，就是返回了一个随机数而已；
link.js - 实现“连接力”，即当两个结点间有边时相互拉拢，但也不能太近；
manyBody.js - 实现“多体”力，用于模拟引力及静电力；
radial.js - “圆环力”，实现半径布局即结点分布在一个圆环上；
simulation.js - 模拟器对象，可以在其上施加多个力；
x.js - “x轴力”，结点固定x坐标；
y.js - “y轴力”，结点固定y坐标；

上面各模块中，最主要的是simulation.js这个模块，它实现了一个完整的模拟器，其它的皆为各种力的实现，所以要看代码要从它开始。

下面我们来深入分析d3.js的实现：
首先我们来看simulation.js这个模块，这个是模拟器的主类，里面实现了力引导的几乎全部流程，除了各种力的具体计算，剩下的其它文件实现了这些力。所有的操作就是从实例化一个simulation对象开始。
我们知道布局的过程是在模拟一个物理过程，反复的计算力然后移动位置，迭代该过程直至达到稳定状态，我们来看这个过程在代码中的体现：
我们一般是这样定义一个模拟器对象的：var simulation = d3.forceSimulation().nodes(nodes_data);，我们知道在js中对象是用函数实现的，进入forceSimulation这个函数（在webstorm中按住ctrl点击它）跳转到exports.forceSimulation = simulation;可以看出forceSimulation是simulation的别名，进入真正的对象simulation，看这个函数的第9行：stepper = timer(step)，这里定义了一个定时器，回调函数为step()，继续看它：

function step() {
    tick();
    event.call("tick", simulation);
    if (alpha < alphaMin) {
      stepper.stop();
      event.call("end", simulation);
    }
}

上面的代码实现了反复执行step这个函数，这个函数里面就是一次计算受力及移动结点
先执行tick()这个函数，这个函数即计算各种力的合力然后移动结点，下面alpha < alphaMin的判断，即退出条件。上面已经可能看出整个力引导算法的脉络了，只是其中的细节还没有展开。
event.call("tick", simulation);这句是调用用户注册的事件函数，比如模拟器每次更新了结点的位置需要反应到界面上，就可以在这个函数里面实现，下面的三句说过了：是判断alpha是否小于alphaMin，是则停止模拟器定时器，调用用户注册的事件回调函数

下面继续深挖tick()函数：

function tick() {
    var i, n = nodes.length, node;


    alpha += (alphaTarget - alpha) * alphaDecay;


    forces.each(function(force) {
      force(alpha);
    });


    for (i = 0; i < n; ++i) {
      node = nodes[i];
      if (node.fx == null) node.x += node.vx *= velocityDecay;
      else node.x = node.fx, node.vx = 0;
      if (node.fy == null) node.y += node.vy *= velocityDecay;
      else node.y = node.fy, node.vy = 0;
    }
}

  看上面的代码，注意alpha += (alphaTarget - alpha) * alphaDecay;这里由于一般alphaTarget是小于alpha，所以这里的+=其实是在减小alpha，即每迭代一次就减少一点直到alphaMin停止，接着这三句：
forces.each(function(force) {
force(alpha);
});
这里对forces进行迭代，对里面的每一个元素调用其force方法。之所以有多个，是因为一个模拟器中是可以叠加多个力的，比如一个“向心力”，加一个“静电力”，再加一个“连接力”，一般在实际应用中需要对多个力进行叠加、反复调试才可以得到想要的效果。这里计算出所有力的合力在x及y方向上的分量，保存在结点的vx,vy属性中。接下来就是利用计算好的力更新结点位置了

for (i = 0; i < n; ++i) {
      node = nodes[i];
      if (node.fx == null) node.x += node.vx *= velocityDecay;
      else node.x = node.fx, node.vx = 0;
      if (node.fy == null) node.y += node.vy *= velocityDecay;
      else node.y = node.fy, node.vy = 0;
}

    迭代所有结点，node.fx == null表示没有设置这个结点的固定位置，fx的意思是“fixed x”，相反如果设置了固定位置则结点不受模拟器内力的影响。
    移动结点的位置是通过node.x += node.vx *= velocityDecay实现的，node.vx是结点在x方向上的受力，velocityDecay代码移动的速度，这是一个配置项。这里直接将受力与位置关联起来其实是合理的，高中物理我们学过力越大则加速度越大，从而在相同时间内达到的速度越大，进而位移越大。同理y分量。
到这里，从计算受力到移动结点整个流程就完了。


上面我们并没有看到合力具体是怎么计算出来的，只是调用了注册到模拟器的各个力的force()方法。该方法会依照一些配置参数及结点当前所处的位置，计算出结点此时在x方向及y方向上的力的分量，反应到结点的xv,xy属性中，下面我们以“连接力”为例子分析，
var link_force =  d3.forceLink(links_data).strength(1).id(function(d){return d.name;});
上面的代码创建了一个连接力对象
simulation.force("links",link_force);
上面的代码将该力施加到模拟中
下面我们来看forceLink.force方法

function force(alpha) {
    for (var k = 0, n = links.length; k < iterations; ++k) {
      for (var i = 0, link, source, target, x, y, l, b; i < n; ++i) {
        link = links[i], source = link.source, target = link.target;
        x = target.x + target.vx - source.x - source.vx || jiggle();
        y = target.y + target.vy - source.y - source.vy || jiggle();
        l = Math.sqrt(x * x + y * y);
        l = (l - distances[i]) / l * alpha * strengths[i];
        x *= l, y *= l;
        target.vx -= x * (b = bias[i]);
        target.vy -= y * b;
        source.vx += x * (b = 1 - b);
        source.vy += y * b;
      }
    }
  }

上面的代码遍历了所有边，对于每一条边，都计算这条边的两个结点的受力，关键代码是下面一行：
l = (l - distances[i]) / l * alpha * strengths[i];
其中l为两结点间的距离，distances为配置的边的长度，alpha与strengths也基本为常量，所以当距离与配置的边长相等时受力为零，否则都会出现引力或斥力，这就是所谓的弹簧力，遵守胡克定律。一句说就是你配置了一个弹簧的长度，把连接两个结点的边想象成弹簧，当拉得太长时会有一个力把它们拉拢，当太短时弹簧被压缩会将它们推开。其它的力基本也同理，就是运用一些物理上的受力公式进行计算。

• 在进行力布局的时候，我们可以通过两种方式来定制自己的布局，一种是选择d3.js给我们预置的各种力，比如forceX是固定在X轴的力，另外我们也可以在注册的tick事件中修正结点的x,y坐标。
• 整个d3.js force的实现，做到了逻辑模型与界面的分离，这样的好处是界面部分可以使用其它的实现方案，比如现在使用的svg，以后出于性能考虑以后可以换成canvas，而内部布局引擎不用做任何改变。
• 我们可以通过响应tick事件来将布局引擎中的数据反应到界面上，同理界面上的拖动操作也可以通过更改模型中的结点位置来实现。

参考
D3.js force帮助文档：https://github.com/d3/d3-force/blob/master/README.md
D3.js force源代码：https://github.com/d3/d3-force/tree/master/src
Verlet积分：https://en.wikipedia.org/wiki/Verlet_integration
力引导算法：https://en.wikipedia.org/wiki/Force-directed_graph_drawing
力引导算法的一个实现：https://blog.csdn.net/newworld123made/article/details/51443603