线性/非线性规划问题求解

线性/非线性规划问题求解

一、用Excel和python编程完成线性规划问题的求解。
1.1、Excel求解对媒体组合问题进行求解
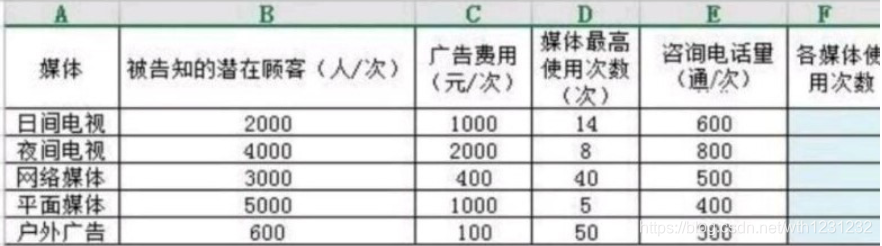
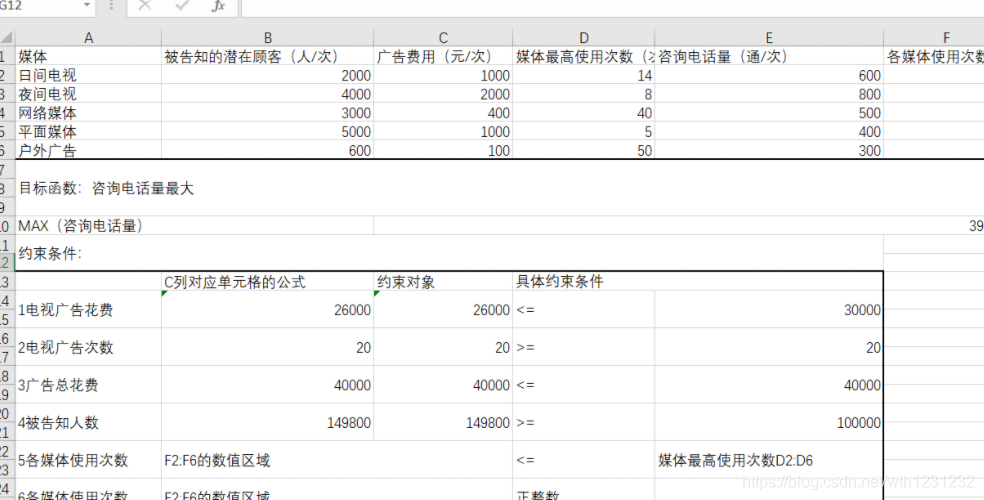
1、建立数据源，将数据录入Excel中：

并增加各媒体使用次数列。

3、在Excel中设置目标函数
由前面的分析可知，目标函数为E2:E6与F2:F6区域两列数组对应元素的乘积之和，在C10单元格中输入“=SUMPRODUCT(E2:E6,F2:F6)”。

4、设置约束条件
降低而不重的·约束条件表达式设置在Excel中。


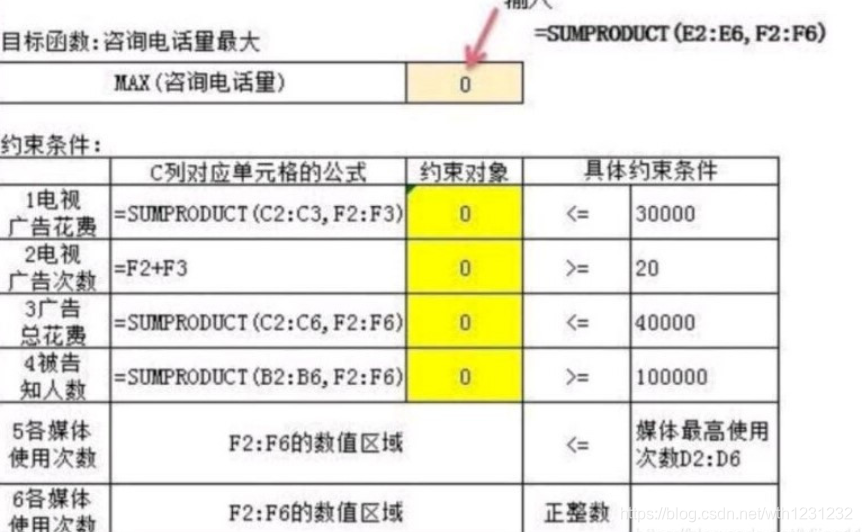
注意：约束对象中填入的也是和C列对应单元格的公式是一样的。
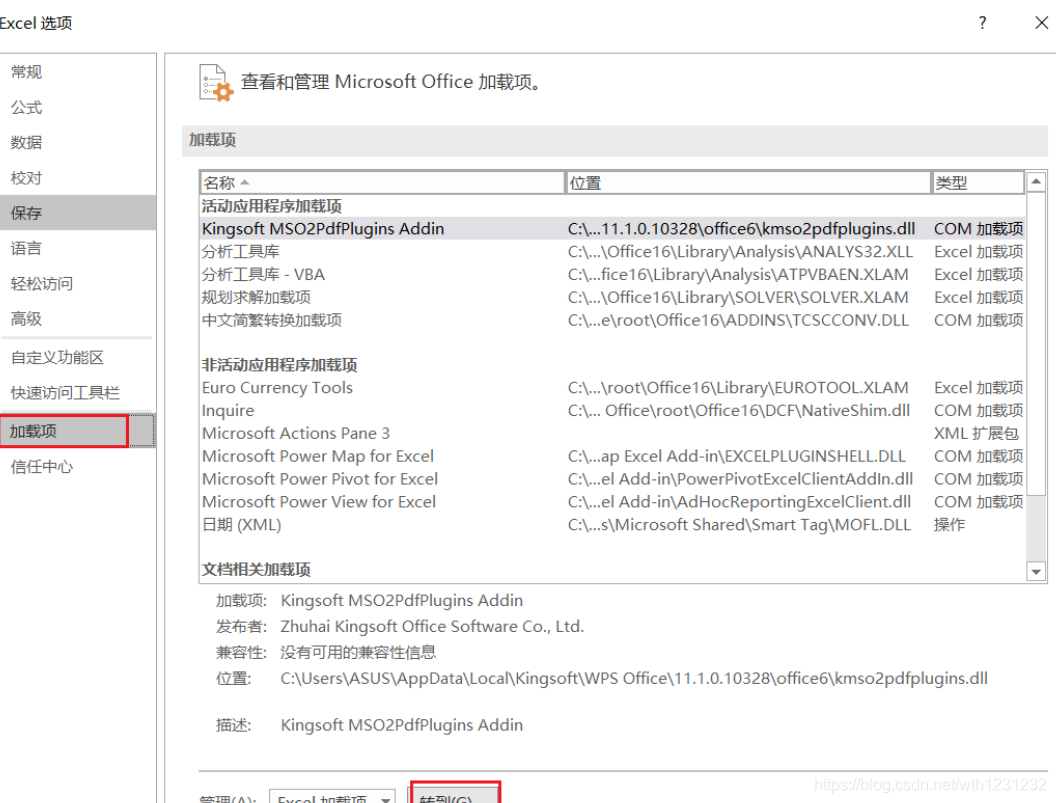
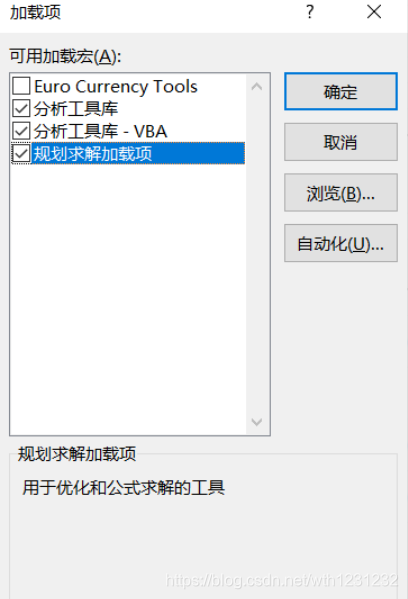
5、加载Excel的规划求解模块
选择“文件→选项→加载项→转到”，勾选“规划求解加载项”，就会在“数据”菜单下出现“规划求解”模块。


6、在规划求解模块中设置决策变量和目标函数
选择“数据→规划求解”

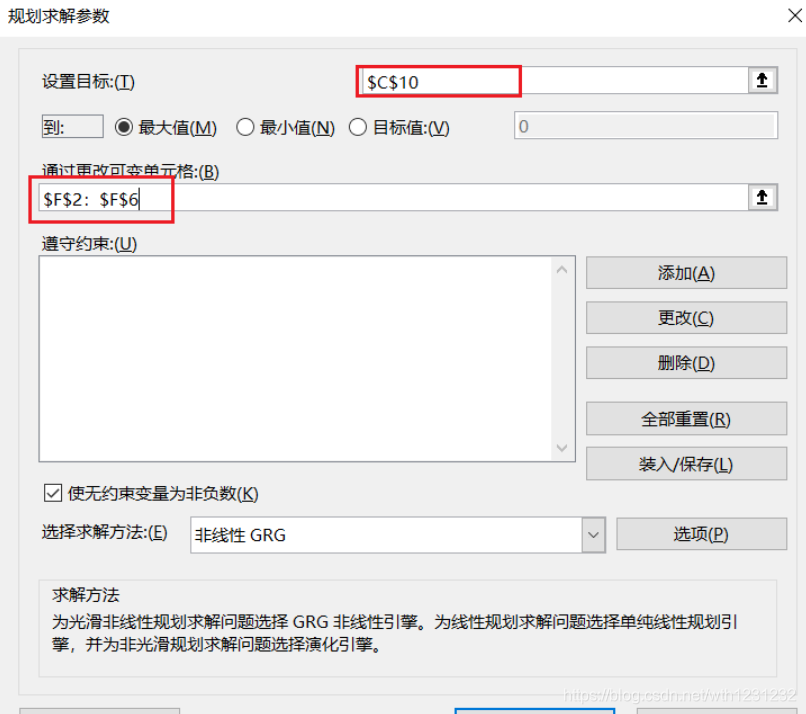
7、设置规划条件
在上一步“数据→规划求解”中设置完后，选择添加

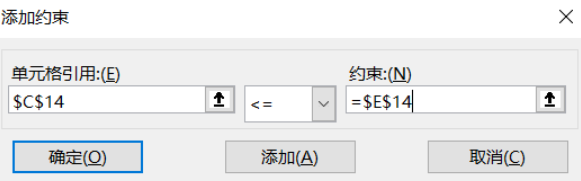
同上依次录入所有约束条件：


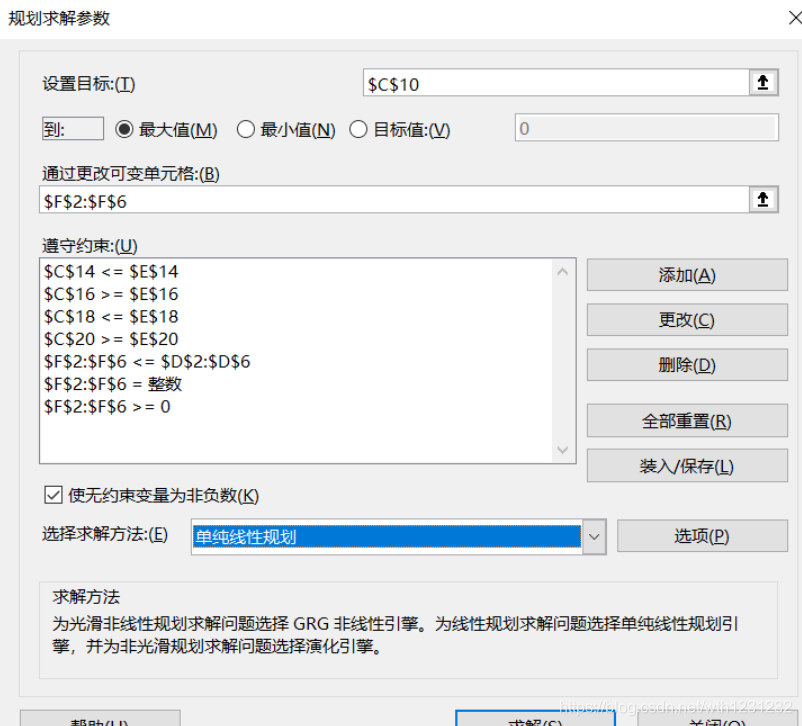
2、Python求解
代码：

from sympy import *
x,y,z,k = symbols('x,y,z,k')
a,b,c=symbols('a,b,c')
f = 8*x*y*z
g = x**2/a**2+y**2/b**2+z**2/c**2-1
L=f+k*g
dx = diff(L, x)   # 对x求偏导
print("dx=",dx)
dy = diff(L,y)   #对y求偏导
print("dy=",dy)
dz = diff(L,z)   #对z求偏导
print("dz=",dz)
dk = diff(L,k)   #对k求偏导
print("dk=",dk)
dx= 8*y*z + 2*k*x/a**2
dy= 8*x*z + 2*k*y/b**2
dz= 8*x*y + 2*k*z/c**2
dk= -1 + z**2/c**2 + y**2/b**2 + x**2/a**2
m= solve([dx,dy,dz,dk],[x,y,z,k])   
print(m)
x=sqrt(3)*a/3
y=sqrt(3)*b/3
z=sqrt(3)*c/3
k=-4*sqrt(3)*a*b*c/3
f = 8*x*y*z
print("方程的最大值为：",f)

得到答案