哈希表

最新推荐文章于 2023-04-29 21:00:42 发布
最新推荐文章于 2023-04-29 21:00:42 发布
阅读量753 收藏 1
点赞数
分类专栏： 算法与数据结构

一、基本概念

散列技术：在记录的存储位置和它的关键字之间建立一个确定的对应关系f，使得每个关键字key对应一个存储位置f(key)。

f：散列函数/哈希函数；
采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间称为散列表或哈希表。
关键字对应的记录存储位置称为散列地址。

散列技术既是一种存储方法，也是一种查找方法。
散列技术适合求解问题是查找与给定值相等的记录。查找速度快。
散列技术不适合范围查找，不适合查找同样关键字的记录，不适合获取记录的排序，最值。

冲突：关键字key1不等于key2，但f(key1)=f(key2)。
把key1和key2称为散列函数的同义词。

二、散列函数构造

两个原则：

  1. 计算简单
  2. 散列地址分布均匀

1. 直接定址发

f(key)=a x key+b(a、b为常数)

简单，均匀，不会冲突，但是事先知道关键字的分布情况，适合查找表小且连续。

2. 数字分析法

关键字位数多，比如手机号，可能前几位一样，只是后几位不同，抽取关键字的一部分计算散列存储位置。事先知道关键字分布且若干位分布均匀。
这里写图片描述

3. 平方取中法

不知道关键字分布，且位数不是很大。1234，平方1522756，抽取中间227作为散列地址。

4. 折叠法

不知道关键字分布，位数多。
从左到右分割成位数相等的几部分，这几部分叠加求和，并按散列表表长，取后几位作为散列地址。

5. 除留余数法

散列表长m

f(key)=key mod p(p<=m)

p选取不好，产生冲突。
通常p为<=m（最好接近m）的最小质数或者不包含小于20质因子的合数。

6. 随机数法

关键字长度不等。

f(key)=random(key),random随机函数

当关键字为字符串，转化为某种数字来对待，比如ASCLL码或者Unicode码等。

三、散列冲突处理

1. 开放定址法

又叫线性探测法：一旦冲突，寻找下一个空的散列地址。散列表大。
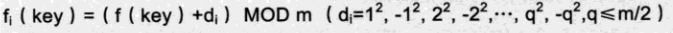
这里写图片描述

优化：二次探测法
这里写图片描述
双向寻找，防止后面没空，但前面有空。
增加平方，不让关键字聚集在某一块区域。

还有对位移量d随机函数计算，称之为随机探测法。

2. 再散列函数法

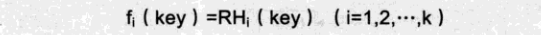
这里写图片描述
RHi不同散列函数，随机使用除留、折叠、平方，每次冲突换种散列函数。

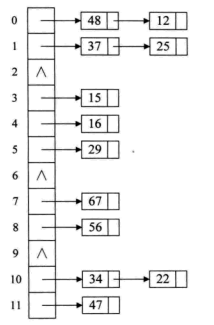
3. 链地址法

将所有关键字为同义词的记录存储在一个单链表（同义词字表）中。
散列表中只存储所有同义词字表的头指针。
{12,67,56,16,25,37,22,29,15,47,48,34} mod 12
这里写图片描述

缺点：单链表查找遍历耗时。

4. 公共溢出区法

冲突关键字存储到溢出表中
这里写图片描述
散列计算后，先基本表比较。不等，到溢出表进行顺序查找。

四、散列表查找

1. 附加源码

<code class="language-c hljs  has-numbering"><span class="hljs-preprocessor">#include "stdio.h"    </span>
<span class="hljs-preprocessor">#include "stdlib.h"   </span>
<span class="hljs-preprocessor">#include "io.h"  </span>
<span class="hljs-preprocessor">#include "math.h"  </span>
<span class="hljs-preprocessor">#include "time.h"</span>

<span class="hljs-preprocessor">#define OK 1</span>
<span class="hljs-preprocessor">#define ERROR 0</span>
<span class="hljs-preprocessor">#define TRUE 1</span>
<span class="hljs-preprocessor">#define FALSE 0</span>

<span class="hljs-preprocessor">#define MAXSIZE 100 /* 存储空间初始分配量 */</span>

<span class="hljs-preprocessor">#define SUCCESS 1</span>
<span class="hljs-preprocessor">#define UNSUCCESS 0</span>
<span class="hljs-preprocessor">#define HASHSIZE 12 /* 定义散列表长为数组的长度 */</span>
<span class="hljs-preprocessor">#define NULLKEY -32768 </span>

<span class="hljs-keyword">typedef</span> <span class="hljs-keyword">int</span> Status; <span class="hljs-comment">/* Status是函数的类型,其值是函数结果状态代码，如OK等 */</span> 

<span class="hljs-keyword">typedef</span> <span class="hljs-keyword">struct</span>
{
   <span class="hljs-keyword">int</span> *elem; <span class="hljs-comment">/* 数据元素存储基址，动态分配数组 */</span>
   <span class="hljs-keyword">int</span> count; <span class="hljs-comment">/*  当前数据元素个数 */</span>
}HashTable;

<span class="hljs-keyword">int</span> m=<span class="hljs-number">0</span>; <span class="hljs-comment">/* 散列表表长，全局变量 */</span>

<span class="hljs-comment">/* 初始化散列表 */</span>
Status InitHashTable(HashTable *H)
{
    <span class="hljs-keyword">int</span> i;
    m=HASHSIZE;
    H->count=m;
    H->elem=(<span class="hljs-keyword">int</span> *)<span class="hljs-built_in">malloc</span>(m*<span class="hljs-keyword">sizeof</span>(<span class="hljs-keyword">int</span>));
    <span class="hljs-keyword">for</span>(i=<span class="hljs-number">0</span>;i<m;i++)
        H->elem[i]=NULLKEY; 
    <span class="hljs-keyword">return</span> OK;
}

<span class="hljs-comment">/* 散列函数 */</span>
<span class="hljs-keyword">int</span> Hash(<span class="hljs-keyword">int</span> key)
{
    <span class="hljs-keyword">return</span> key % m; <span class="hljs-comment">/* 除留余数法 */</span>
}

<span class="hljs-comment">/* 插入关键字进散列表 */</span>
<span class="hljs-keyword">void</span> InsertHash(HashTable *H,<span class="hljs-keyword">int</span> key)
{
    <span class="hljs-keyword">int</span> addr = Hash(key); <span class="hljs-comment">/* 求散列地址 */</span>
    <span class="hljs-keyword">while</span> (H->elem[addr] != NULLKEY) <span class="hljs-comment">/* 如果不为空，则冲突 */</span>
    {
        addr = (addr+<span class="hljs-number">1</span>) % m; <span class="hljs-comment">/* 开放定址法的线性探测 */</span>
    }
    H->elem[addr] = key; <span class="hljs-comment">/* 直到有空位后插入关键字 */</span>
}

<span class="hljs-comment">/* 散列表查找关键字 */</span>
Status SearchHash(HashTable H,<span class="hljs-keyword">int</span> key,<span class="hljs-keyword">int</span> *addr)
{
    *addr = Hash(key);  <span class="hljs-comment">/* 求散列地址 */</span>
    <span class="hljs-keyword">while</span>(H.elem[*addr] != key) <span class="hljs-comment">/* 如果不为空，则冲突 */</span>
    {
        *addr = (*addr+<span class="hljs-number">1</span>) % m; <span class="hljs-comment">/* 开放定址法的线性探测 */</span>
        <span class="hljs-keyword">if</span> (H.elem[*addr] == NULLKEY || *addr == Hash(key)) <span class="hljs-comment">/* 如果循环回到原点 */</span>
            <span class="hljs-keyword">return</span> UNSUCCESS;   <span class="hljs-comment">/* 则说明关键字不存在 */</span>
    }
    <span class="hljs-keyword">return</span> SUCCESS;
}

<span class="hljs-keyword">int</span> main()
{
    <span class="hljs-keyword">int</span> arr[HASHSIZE]={<span class="hljs-number">12</span>,<span class="hljs-number">67</span>,<span class="hljs-number">56</span>,<span class="hljs-number">16</span>,<span class="hljs-number">25</span>,<span class="hljs-number">37</span>,<span class="hljs-number">22</span>,<span class="hljs-number">29</span>,<span class="hljs-number">15</span>,<span class="hljs-number">47</span>,<span class="hljs-number">48</span>,<span class="hljs-number">34</span>};
    <span class="hljs-keyword">int</span> i,p,key,result;
    HashTable H;

    key=<span class="hljs-number">39</span>;

    InitHashTable(&H);
    <span class="hljs-keyword">for</span>(i=<span class="hljs-number">0</span>;i<m;i++)
         InsertHash(&H,arr[i]);

    result=SearchHash(H,key,&p);
    <span class="hljs-keyword">if</span> (result)
        <span class="hljs-built_in">printf</span>(<span class="hljs-string">"查找 %d 的地址为：%d \n"</span>,key,p);
    <span class="hljs-keyword">else</span>
        <span class="hljs-built_in">printf</span>(<span class="hljs-string">"查找 %d 失败。\n"</span>,key);

    <span class="hljs-keyword">for</span>(i=<span class="hljs-number">0</span>;i<m;i++)
    {
        key=arr[i];
        SearchHash(H,key,&p);
        <span class="hljs-built_in">printf</span>(<span class="hljs-string">"查找 %d 的地址为：%d \n"</span>,key,p);
    }

    <span class="hljs-keyword">return</span> <span class="hljs-number">0</span>;
}
</code>

2. 查找性能

如果无冲突，O(1)。
查找平均长度取决于：

  • 散列函数是否均匀
  • 处理冲突的方法
  • 散列表的装填因子
    装填因子=填入表中的记录个数/散列表长度。（表示散列表的装满的程度）
    当填入表中的记录越多，装填因子越大，产生冲突可能性越大。

通常将散列表的空间设置的比查找集合大，牺牲空间换时间。

wwj_zy
关注
专栏目录
哈希表(C语言实现)
2303_82176667的博客
09-21 992
首先，我们将key 和value 封装成一个类Pair ，以表示键值对。//键值对int key;int *val;}Pair;其次，我们来定义哈希表的结构体// 基于数组实现哈希表//键值对int key;int *val;} Pair;//链表节点Pair* pair;}Node;//哈希表节点定义int size;//键值对的数量//哈希表的容量//触发扩容的负载因子阈值//扩容倍数//桶数组。
TOP K
我帅故我在
08-05 756
出处： http://blog.csdn.net/v_july_v/article/details/6256463 问题描述 百度面试题：     搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。     假设目前
不包含小于20的质因数的合数？(防止题目重复)
qq_45591813的博客
11-11 828
不包含小于20的质因数的合数？ 比如667，它的因数只有1、23、29、667，其中1和667都不是质因数
哈希表课程设计数据结构实验报告——哈希表设计
07-05
哈希表课程设计数据结构实验报告——哈希表设计 针对某个集体中的人名设计一个哈希表，使得平均查找长度不超过R，完成相应的建立和查表程序. 1.2 人名为汉语拼音形式，最长不超过18个字符(如：庄双双 ...
hashtab2_C语言_哈希表删除、添加、寻找_codeblocks_
10-04
哈希表是一种高效的数据结构，它通过特定的函数（哈希函数）将数据映射到一个固定大小的数组中，以此实现快速的查找、插入和删除操作。在C语言中，我们可以手动构建哈希表来处理这些操作。Code::Blocks是一款流行的...
哈希表实验C语言版实现
09-05
哈希表是一种高效的数据结构，它通过特定的哈希函数将键（Key）映射到一个固定大小的数组中，从而实现快速的插入、查找和删除操作。在本实验中，哈希表的C语言实现主要涉及以下几个核心知识点： 1. **哈希表的基本...
数据结构实验五哈希表设计c语言
04-25
哈希表设计与实现 哈希表是一种常用的数据结构，它可以快速地存储和检索数据。在本实验中，我们设计了一种哈希表，以学生姓名为关键字，存储学生信息，并实现了查找学生信息的功能。 哈希表的构造方法 在本实验中...
哈希表——基本概念
lhy_601的博客
09-02 2678
一、概念哈希表，又称为散列表，是一种根据键来直接访问内存位置的一种数据结构。它通过一个计算键值的函数（散列函数）来将所查询的数据映射到哈希表中的一个位置来查找该位置的内容，从而达到快速查找的目的。（存放记录的数组就称为哈希表）。 若关键字为k，则其值就存放在f(k)对应的位置上，这样可以实现不用比较就可以直接找到要求的记录，其中f(k)就是散列函数 冲突：对于不同的关键字可能得到相同的散列地址，这就
散列表的查找技术
qq_35577488的博客
12-12 467
一.基本思想所谓查找，其实质就是要确定待查记录在查找结构中的存储位置 , 以往的查找结构中，查找记录和存储位置之间并没有确定的关系。而最理想的情况是不经过任何比较，就能够得到待查记录的存储位置。那就必须在查找记录和存储位置之间建立确定的关系H。使得每个关键码key和唯一的存储地址H(key)对应起来.这个过程叫映射这种查找技术称为散列技术，存储的连续空间称为散列表 , 将关键码映射为散列表中合适...
哈希表及哈希表查找相关概念（转）
weixin_30535843的博客
10-16 396
1. 哈希表的概念　　　对于动态查找表而言，1) 表长不确定；2)在设计查找表时，只知道关键字所属范围，而不知道确切的关键字。因此，一般情况需建立一个函数关系，以f(key)作为关键字为key的录在表中的位置，通常称这个函数f(key)为哈希函数。(注意：这个函数并不一定是数学函数)　1. 哈希函数是一个映象，即：将关键字的集合映射到某个地址集合上，它的设置很灵活，只要这个地址集合的大小不超出允许...
数据结构：哈希表（除留取余法--线性探测法）
憧憬，思考，奋斗，飞翔
05-08 8771
#include #include using namespace std; #define SUCCESS 1 #define UNSUCCESS 0 #define HASHSIZE 12 #define NULLKEY 0xffffffff/2 typedef struct { int *elem; int count; }HashTable; typedef int Sta
【数据结构】哈希表
最新发布
qq_48479056的博客
04-29 6304
通过上述操作：将数组的具体数值转化为了新布尔数组的下标，此时要查找某个元素，在新数组中已经知道了该数组的索引下标，因此查找起来非常快。但是这样也有一个问题，就是如果我这个数组中的数据范围很分散，比如[10,100000,1000000000]这种，那我最少要创建一个1000000000+1大小长度的新数组，太不划算了。JDK中的HashMap的factor默认是0.75，而在阿里的实验室论证中，在一般的商用系统中，factor为10是比较合适的设置。比较好的方式就是n取素数，这样能显著降低哈希碰撞的概率。
数据结构 Hash表解读（哈希表）
Lizhj的博客
08-18 528
参考链接：https://blog.csdn.net/u011109881/article/details/80379505 一、什么是Hash表 要想知道什么是哈希表，那得先了解哈希函数 哈希函数 对比之前博客讨论的二叉排序树 二叉平衡树 红黑树 B B+树，它们的查找都是先从根节点进行查找，从节点取出数据或索引与查找值进行比较。那么，有没有一种函数H，根据这个函数和查找关键字key，可以直接确定查找值所在位置，而不需要一个个比较。这样就**“预先知道”**key所在的位置，直接找到数据，提升效率。
Hash 哈希表
m0_52343363的博客
04-23 1349
我们学习了数据结构,其实都在做一件事情那就是 数据的结构 无论是学了啥？目的都是为了1.1 哈希表的定义（Hash table，也叫哈希表），是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。remark: 通过某种映射关系 比方将你映射为 阿兰图灵 那么在这个名人散列表查找到图灵时就等于找到了你。
哈希表实现与查找操作
"哈希表实例" 哈希表是一种数据结构，它提供了快速的数据存取方式，通过将数据的关键字（Key）映射到一个固定大小的数组索引上实现。在本实例中，哈希表被定义为一个结构体`HashTable`，包含了元素存储的数组`elem`...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值