【数学都知道】  精选
精选
作者:蒋迅
购买请到“好玩的数学”微店:

店主子曰一直在他的微信公共号里为大家提供有趣的作品。希望大家支持他一下。


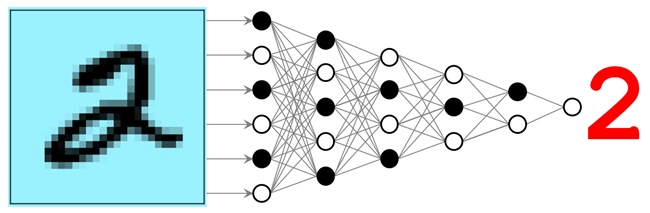
深入学习对图像处理,数学和人性的影响。 “你的孙子可能有一个机器人配偶。”

免费阅读图书,作者是瑞典的两位学者。

受“托里拆利小号”的启发,作者做了这个动图。

篮球比赛的投球和垒球里的投球,都让好奇,他们怎么投得那么准呢?这里面有没有数学的贡献呢?

- Simple Proof of the Prime Number Theorem
Fascinating Facts and Conjectures about Primes and Other Special Nu...
Factoring Massive Numbers: Machine Learning Approach
How and Why: Decorrelate Time Series
Distribution of Arrival Times of Extreme Events
The Fundamental Statistics Theorem Revisited
88 percent of all integers have a factor under 100
Math Challenge: Computing the Average Rotational Speed of Earth
Representation of Numbers as Infinite Products
A Beautiful Probability Theorem
Mars Craters: An Interesting Stochastic Geometry Problem
The art and (data) science of leveraging economic bubbles
Seasons in Binary Star Planetary Systems
二者看似毫不相关,但它们有惊奇的类比。李超老师告诉你。

超复合分形,体素分形,光栅图形,复值魏尔斯特拉斯函数,多维缩放
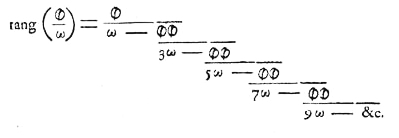
约翰·海因里希·朗伯(1728-1777)于1761年证明了PI是无理数,那年他33岁。

Douady兔是一个为法国人Adrien Douady(1935-2006)命名的分形。看翻译:
http://datamarket.atman360.com

逼近论中的一个
问题。如果你有一个序列逼近一个函数,你想知道逼近的零点和极点在哪里。
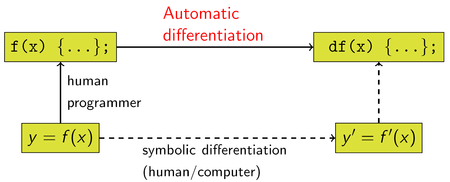
在数学和计算机代数中,自动微分 (
Automatic differentiation) 有时称作演算式微分, 是一种可以借由计算机程序计算一个函数导数的方法。两种传统做微分的方法为:一,对一个函数的表示式做符号上的微分,并且计算其在某一点上的值。二,使用差分。
别告诉我你都知道。相关连接:
物理中数论

全息原理(
Holographic principle),是弦论与预期中的量子引力的性质之一,描述了一个空间的性质可编码在其边界上,例如事件视界的类光边界。相关连接:
NASA图片

介绍过这个。十个数学方程,十个展框,代表了美丽、和谐。
-
Tutorial: How to detect spurious correlations - and how to find the real ones
-
How to Lie with Visualizations - Statistics, Causation vs Correlation
-
Associations and Correlations: The Essential Elements - Book
-
Excluding variables from a logistic regression model - based on correlation

比较pi^e 和 e^pi有不同的办法。现在要求不用计算。作图很直接,
看图。

第一次听说这个杂志,为它叫个好。
任意一个自然数
n都可以写成三个平方数的和的充分必要条件是:
n 不能写成 4
a(8
b + 7) 的形式,这里
a和
b 是整数。

为了研究秘鲁
纳斯卡巨画,Maria Reiche在秘鲁沙漠里生活了40年。
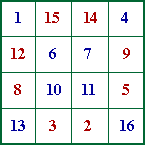
想不想自己创作出幻方来?到这里学一学吧。相关阅读:
幻方

双曲余弦的图形称为悬链线。它具有这样的性质。

轨形,也称“轨道流形”,是
流形的一个推广,允许某种"奇异点"在其拓扑中存在。大致来讲,它是局部看起来像一些简单空间(例如,欧几里得空间)通过各种有限群的群作用的商。奇点对应于群作用的不动点,而作用必须在某种意义下相容。
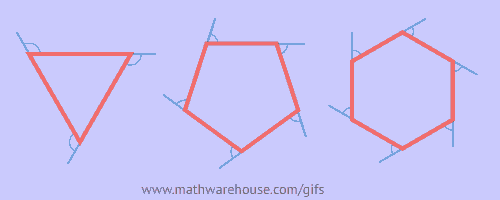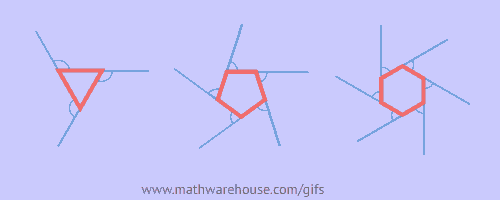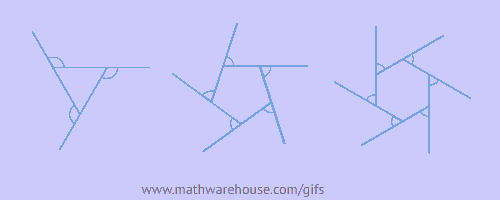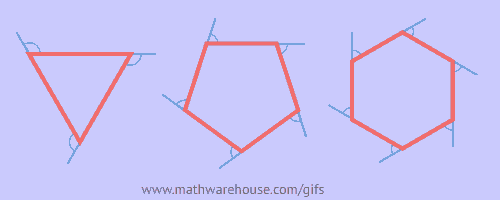
这里收集了一些挺不错的数学动图。

希望你能找到你的归属,否则你就out了。
他们说是:Alexander Grothendieck,Thurston,Gromov,Terence TaoSir Michael Atiyah,Serge Lang,John Baez,John Willard Milnor,…Martin Gardner算吗?中国人大概会说陶哲轩吧?
计算机正在赢得各种游戏,但下一个是数学。数学也是一个游戏,数学家正在玩“严格证明”的游戏。计算机能赢的了吗?
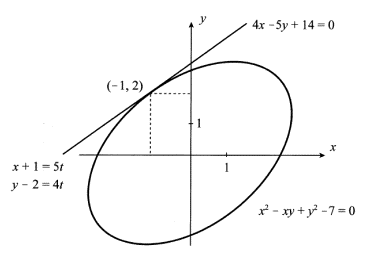
分析方法足以找到圆锥曲线的切线方程。

有没有缺什么?一定有的。

马尔科夫蒙特卡洛(MCMC)方法(含随机游走蒙特卡洛方法)是一组用马氏链从随机分布取样的算法,之前步骤的作为底本。步数越多,结果越好。
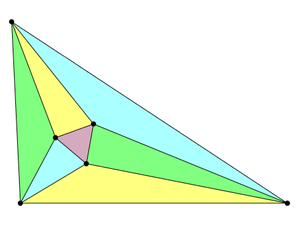
在欧几里得几何中,莫雷角三分线定理(Morley's theorem)说明对所有的三角形,其三个内角作角三分线,靠近公共边三分线的三个交点,是一个等边三角形。此定理由法兰克·莫雷在1899年发现。对外角作外角三分线,也会有类似的性质,可以再出4个等边三角形。此定理有趣的地方是我们没办法用尺规作图作出其等边三角形,因为已经证明出尺规作图无法作出三等分角。相关阅读:
Morley's Miracle J. Arioni's Proof
通过直观的动画演示,教你从变换的视角来看黎曼ζ函数,揭晓解析延拓背后优美的几何直觉,最后简要介绍与黎曼ζ函数相关的千禧年大奖难题“黎曼猜想”。
斐波那契可以有很多种推广,比如负数、复数、向量等等。还有类似于斐波那契数列的整数数列,…
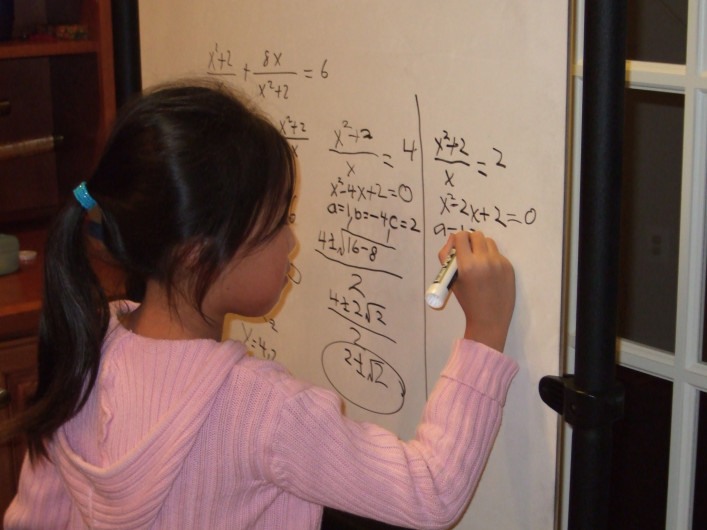
17岁的斯蒂芬妮□梅在高中毕业之前就从乔治梅森大学获得了数学硕士学位。一切都始于教学卡片。梅还记得和爸爸一起用卡片做练习。“他教我做加法、乘法和减法,”她说道。那是在幼儿园的时候。到一年级的时候,她就开始学习代数。二年级的时候,学习几何。星期六,这位弗吉尼亚少女将获得乔治梅森大学数学专业的理学硕士学位。她的下一站是纽约大学,她将在那里攻读博士学位。相关连接:
PPT,
中文翻译
哆嗒作品
女神艾米的美妙数学
英国专家:中国数学教学体系能促进社会阶层流动
三本数学史哲书,帮你理解数学思想的进化
数学奖章上的数学故事──讲讲国际数学家大会四大奖项
惊!歌德巴赫、孪生素数猜想还可以这样玩!

520:向你心中的数学家表白吧!

征文活动颁奖公告
在数学里是不会上当受骗的
数学实现正义的经典案例:Peoples v. Collins案
六一儿童节:看看这10个数学家的逆天童年
英国专家:中国数学教学体系能促进社会阶层流动
三本数学史哲书,帮你理解数学思想的进化
数学奖章上的数学故事──讲讲国际数学家大会四大奖项
惊!歌德巴赫、孪生素数猜想还可以这样玩!

520:向你心中的数学家表白吧!

征文活动颁奖公告
在数学里是不会上当受骗的
数学实现正义的经典案例:Peoples v. Collins案
六一儿童节:看看这10个数学家的逆天童年
人物与历史
川大数学系师生传奇
用概率判生死:法庭上的数学证据
牛顿为什么会相信上帝的存在,原来是三体惹的祸。。。
数学家告诉你林书豪如何影响尼克斯
纳什打造博弈论江山
『约翰·福布斯·纳什』数学大师的如戏人生
陈木法:迈好科学研究的第一步
中国数学竞赛史上最玩命的“赌徒”张筑生,用一个字换来五届IMO总分第

顶级数学家如何做数学?当代大师阿兰·孔涅的探秘之旅
世界科学史上的一段传奇,阿基米德羊皮书在同步辐射实验室中显出真容。。。

氢原子背后隐藏的代数 | 当阿热遇见赛先生
于飞:以哲思演绎数学的精妙

HPM人物谈:怀念沈康身先生

别把我吹捧成伽罗瓦

数学凌驾于一切人类文化之上,向各个知识领域渗透
数学思维比数学运算更重要
王世强先生自述

数学与爱情
大逆不道的诞生,先天不足的缺陷,却成为现代数学的基础 (无穷)
陈景润诞辰 | 陈景润与“哥德巴赫猜想”
37年后妻子重新解读陈景润:他不是不谙世事的科学怪人
液体动力学发展
二十年前,世界最强围棋AI在中国,出自中山大学一位退休教授之手
回归基本原理的数字探索:减法与0的发现
93岁数学教授讲律诗、对联火了,他的一句话掷地有声
康托与老师撕逼十年,还做了34年疯子的数学天才,死前终於得到了认同
柯洁1/4子惜败,机器之心独家对话AlphaGo开发者导师 Martin Muller
COS访谈第28期:陈松蹊教授

从高斯算1+2+3+...+100 谈起
这位华人数学大牛(张寿武)太有趣了,时而虐老师,时而又被老师虐!
【公元前1000 - 元年】- 数学进化史
这位过劳死的天才数学家,一生只发表了10篇论文,钻研了15年数学,却名震天下(黎曼)
端午送书!(《中国数学教育人名辞典》)
用一生完成的证明──记齐民友教授 ( 齐民友:数学教育的改革要遵循数学科学的发展)

沃尔夫勒姆和他的“新科学”(上)
用概率判生死:法庭上的数学证据
牛顿为什么会相信上帝的存在,原来是三体惹的祸。。。
数学家告诉你林书豪如何影响尼克斯
纳什打造博弈论江山
『约翰·福布斯·纳什』数学大师的如戏人生
陈木法:迈好科学研究的第一步
中国数学竞赛史上最玩命的“赌徒”张筑生,用一个字换来五届IMO总分第

顶级数学家如何做数学?当代大师阿兰·孔涅的探秘之旅
世界科学史上的一段传奇,阿基米德羊皮书在同步辐射实验室中显出真容。。。

氢原子背后隐藏的代数 | 当阿热遇见赛先生
于飞:以哲思演绎数学的精妙

HPM人物谈:怀念沈康身先生

别把我吹捧成伽罗瓦

数学凌驾于一切人类文化之上,向各个知识领域渗透
数学思维比数学运算更重要
王世强先生自述

数学与爱情
大逆不道的诞生,先天不足的缺陷,却成为现代数学的基础 (无穷)
陈景润诞辰 | 陈景润与“哥德巴赫猜想”
37年后妻子重新解读陈景润:他不是不谙世事的科学怪人
液体动力学发展
二十年前,世界最强围棋AI在中国,出自中山大学一位退休教授之手
回归基本原理的数字探索:减法与0的发现
93岁数学教授讲律诗、对联火了,他的一句话掷地有声
康托与老师撕逼十年,还做了34年疯子的数学天才,死前终於得到了认同
柯洁1/4子惜败,机器之心独家对话AlphaGo开发者导师 Martin Muller
COS访谈第28期:陈松蹊教授

从高斯算1+2+3+...+100 谈起
这位华人数学大牛(张寿武)太有趣了,时而虐老师,时而又被老师虐!
【公元前1000 - 元年】- 数学进化史
这位过劳死的天才数学家,一生只发表了10篇论文,钻研了15年数学,却名震天下(黎曼)
端午送书!(《中国数学教育人名辞典》)
用一生完成的证明──记齐民友教授 ( 齐民友:数学教育的改革要遵循数学科学的发展)

沃尔夫勒姆和他的“新科学”(上)
卡西尼号会涉及到二十二个轨道,其中轨道的近拱点或者最近点,实际上就在土星大气和环的最内层之间的缝隙里。我们要做的是利用泰坦星最后的引力助推来设计轨迹,重力助推(Gravity assist)就是通常所说的引力弹弓效应,利用行星的引力场来给飞行器加速或减速。
不同地方排队方式不总是一样。很多地方采用的是“蛇形排队法”,在几个柜台同时工作的时候,所有的顾客只排一队,队伍像一条长长的蛇一样在间隔的栅栏之间穿行,排在队伍最前面的顾客就可以得到服务。而有的地方采用的则是传统的,每个柜台后面各自排一队的方式。美国卖汉堡的两家快餐店──Wendy汉堡和麦当劳,就分别使用了蛇形排队法和多列排队法。如果要较个真的话,这两种排队方法孰优孰劣呢?
1,四元数:150年后在计算机时代盛开;2,最密堆积:3个世纪后在信道中相遇;概率论:从赌桌上的硬道理到保险业的发展。英文原文:
The unplanned impact of maths
计算流体力学是以计算机为工具,利用离散化的网格技术和数值计算方法求解流体运动方程,从而揭示流动机理和流动规律的新兴交叉学科。张涵信院士将计算流体力学的研究内容概括为5 个“M”和一个“A”。五个“M”分别是Machine,Mesh, Method, Mechanism 和Mapping。Machine,即计算机,它是CFD 研究的硬件基础,而并行计算技术,尤其是针对大型异构并行计算机的高效并行算法是CFD 与计算机硬件系统密切相关的研究内容;Mesh,即计算网格(或者称Grid),网格划分是整个数值计算的基础和前提,已成为CFD 的重要研究领域,并逐步形成为一个重要的学科分支;Method,即计算方法,流体力学控制方程的求解方法是CFD 中最为活跃的领域,目前已经发展了各种各样的求解方法,如有限差分法(finite difference method, FDM)、有限体积法(finite volume method, FVM)、有限元法(finite element method, FEM) 等;Mechanism,即流动机理,CFD 的最终目的是获得飞行器的气动特性和与之相应的流动机理,如何从数值计算的“数据海洋”中分析流动机理至关重要;Mapping,即流动显示,计算结果以静、动态的图形展示出来,更加方便分析流动机理,揭示流动规律。一个“A”指Application,即应用,CFD 研究的目的是在以航空航天为代表的众多工业领域得到良好的应用,解决航空航天飞行器研制中的关键气动问题。自CFD 诞生以来,始终围绕这五个“M”向前发展,并在实际工程中得到越来越广泛的应用(“A”)。
概率是不确定之事,发生可能性估算的学问。信与不信也是各人的认知。只不过世事无常,哪能尽判黑白,估算之技“知之者胜,不知之者不胜。 ... 多算胜,少算不胜,而况无算乎!”
改革者:为了表示多元系统,引入向量,以便把我们的研究对象从变量扩展到系统。保守者:向量是没有除法的。向量的乘积,内积、外积(点乘,叉乘)不再是向量。改革者:那么,我们来定义向量除法。既然,加法的定义是:“份量的和做和的份量”,我们道法自然,定义除法的定义:“份量的商做商的份量”保守者:定义当然可以定义,但有什么意义呢?改革者:有了向量商,我们可以同时描述系统,以及系统各份量的变化率(是“同时”),并定义变化率为系统的“演替即时趋势”。
股市数据,一个国家、地区的国民经济数据都是这样的多元系统时间链。变量独立,资源共享,时间惯性,指数增长。
在白图格吉扎布的博客中介绍了他提出的关于向量的一种
新乘法。向量各个份量的积对应“乘积运算”而获得的新向量的各个份量。显然这样获得的新份量们构成了一个新的向量。在我这个数学外行的人看,这是一种新的提法。至少对我有新意(它与过去的向量点乘,□乘不同)。作为学生,我在考虑这种做法是否具有应用实例。我想如果这样做不仅没有错误而且又是我们经常可以遇到的运算,那么这个新定义就有很大的实用价值。1. 超市的购物菜单。2. 降水的这个雨量深度与其对应笼罩面积的积。
很多人都认为,现在没有答辩通不过的论文,这是一种误解,这些年,我参与过的研究生论文答辩最终未能通过的很多,几乎每年都有几个。今天有幸参加了一位数学教育博士学位论文的答辩会,这里我要为其导师,一位德高望重的老先生点个大大的赞,他没有因为专家们不认同学生的论文袒护学生,而是要求学生认真修改,过关了再答辩。
程京德:哥德尔不完全性定理的内容和有效范围 (3) 各种典型误解实例
本文将以渐进(未必是以对象文章发表时间为序)方式列举一些对哥德尔不完全性定理的典型误解实例,以正式公开发表的文章为对象。
华罗庚大师是这样讲的,当刚拿到一册书时会感觉很厚,我这里所说的很厚不是物质概念的,而是精神层面的,因为书中的内容或全部、或大多都是陌生的,当然会觉得厚。可读着读着,将书中的陌生变成了熟识,待一册书全部读完了,书就变薄了,因为书中知识的难点都被你给攻克了吗。相关阅读:
陈景润生活中二三事
这里所说的小学高年级学生,包括初中低年级学生,打基础,基础特别好的自然到了中学可以练的少一些,实际上,美国直到高中生都有相应的训练和比赛。
我们把数学,分为概念引入和日常训练,概念引入部分在前,请参考张亚杰的论文,链接见于
我们开创的小学数学新教法
。
日常训练部分,则用奥数教材上的“速算+巧算”就挺好,不过,在美国现在称为
"Number Sense"
,
这是我收录的一些网站链接,上面有免费的测试题,欢迎同好告诉我增录。
当我这几年接触到数学教育,听到这个名词的时候,想问它是什么意思,不过,没有听到太清晰的回答,而且不同层次的数学教育工作者,答法甚至有很大不同。
在柯西的努力下,微积分中一些重要的概念如连续、可导性、微分、积分、无穷级数的和等概念也都有了较为坚实的理论基础。这种分析数学方法,实际上就是在向古希蜡数学精神回归。但是在柯西之后,魏尔斯特拉斯等人发现为极限提出明确定义并没有完全解决第二次数学危机,因为极限的定义会牵涉到实数,而实数仍然是一个未定义概念。
第4章:欧几里得和阿波罗尼斯。本篇记录此章的第12节“阿波罗尼斯的数学著作”。
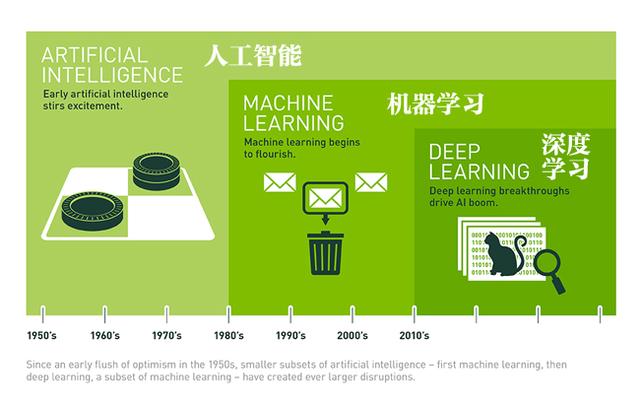
今天的这篇文章主要跟大家讲述人工智能与大学数学(高等数学、线性代数、概率论与数理统计)间密不可分的关系。
有三种产品:小学版、初中版、高中版. 经过讲解。
哥德尔不完全性定理所严格限定的有效范围是很窄的,远不像许多误解随意解释的那么宽。
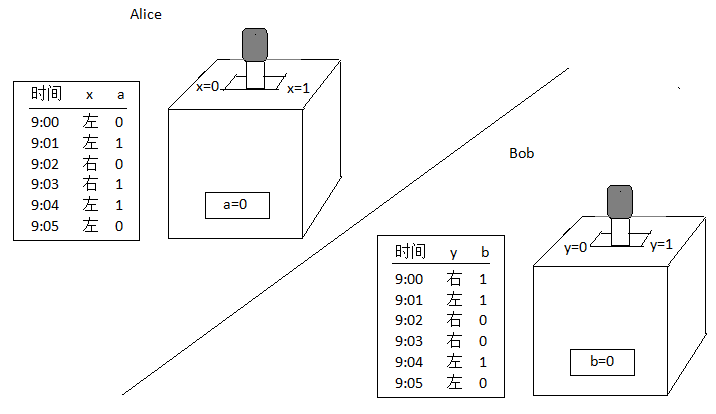
量子纠缠是一种奇妙的现象,物体可以瞬间对远方的另一物体产生影响,但我们它无法利用它来实现超光速通讯。
记得几年前,在纽约时报上讨论如何提高美国的科学教育水平的问题。纽约时报的一位数学专栏的撰稿人,康奈尔大学的数学教授,Steven Strogatze 对这个复杂问题的回答是一句话“找到一位好老师”。这本书就记叙了Strogatze教授和他的高中数学老师Don Joffray先生间长达30年的友谊的故事。相关阅读:
微积分与人生
 地质统计学脱胎于采矿业,当采矿工程师预测将要开采的结果时,特别是当开始获取并能够分析样品,用相应的厚度和影响范围加权计算平均品位时,我们就可以说地质统计学诞生了。地质统计学能有今天的成就,Danie Krige起了至关重要的作用。
地质统计学脱胎于采矿业,当采矿工程师预测将要开采的结果时,特别是当开始获取并能够分析样品,用相应的厚度和影响范围加权计算平均品位时,我们就可以说地质统计学诞生了。地质统计学能有今天的成就,Danie Krige起了至关重要的作用。
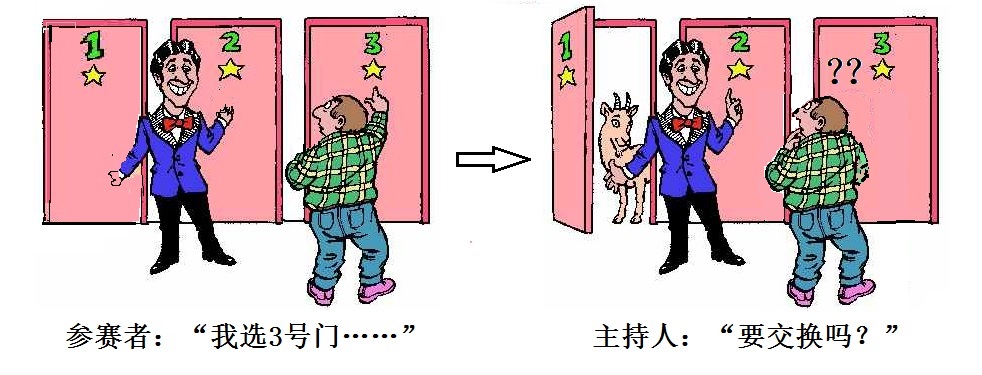
说来令人奇怪,科学定律的发现有时来自于一些毫不起眼,小得不能再小的现象,本福特的发现便是如此:以1开头的数字比较多,这也算是一个定律吗……
在美国,第一次婚姻中有一半以离婚告终。而我国2015年,共有384.14万对夫妻选择离婚。2016年上半年全国依法办理离婚手续的共有168.3万对。目前,我国仅2017年第1季度就已经有95.82万对夫妻离婚。考虑到计划生育导致的适婚人口减少,以及老龄化问题,我国离婚率虽然比不上西方国家,但结果仍让人咋舌。那么,随着现在数学的发展,特别是人工智能、大数据技术的应用,能否提高爱情婚姻的成功率呢?
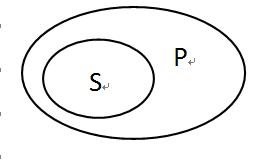
数形结合是数学教学过程中非常重要的思想方法之一,遗憾的是,这种思想在逻辑学中使用的还是不多──准确的说,是数用的不多。或者说,主流的认识还是期望为数学寻找逻辑学的基础而不是相反。
http://blog.sciencenet.cn/blog-420554-1058495.html
上一篇: 【数学都知道】2017年6月1日(纪念吴文俊院士专辑)
下一篇: 管平湖先生与NASA的一次跨越太阳系的合作


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








