贝叶斯推理提供了一种概率(主要应用条件概率)学习手段,根据以往数据的概率分布和已观察到的数据进行推理判断。对数据量大的问题十分适用,在云计算和大数据时代再次成为研究热点。贝叶斯分类器分成两个部分,第一部分对基础知识、贝叶斯决策论、极大似然估计、朴素贝叶斯分类器和半朴素贝叶斯分类器进行介绍,第二部分对贝叶斯网进行详细介绍。本文是对周志华老师的《机器学习》第七章贝叶斯分类器,进行了学习和分析,相当于一篇学习笔记,因此引用了的部分不再进行标注,在文章的最后给出了本文的参考文献。由于作者水平有限错误之处在所难免,望批评指正。
0. 基本知识
为了能更好的理解贝叶斯分类器,本节首先讲述有关概率的基础知识,为后面概率的推到打下基础。
- 加法公式
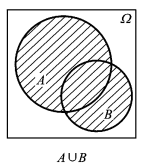
对于任意两个事件A,BA,B,有 P(A∪B)=P(A)+P(B)−P(A∩B)P(A∪B)=P(A)+P(B)−P(A∩B)
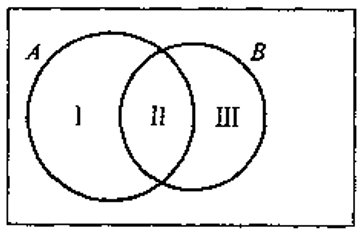
加法公式的示例如图0.1所示,图0.2将AUBAUB分成两两不相容的三个事件I、II、IIII、II、III,则有,
A∪B=I∪II∪III,A∪B=I∪II∪III,
A=I∪II,A=I∪II,
B=II∪III,B=II∪III,
于是,P(A∪B)=P(I)+P(II)+P(III)=P(A)+P(B)−P(A∩B).P(A∪B)=P(I)+P(II)+P(III)=P(A)+P(B)−P(A∩B).
图0.1 两个事件的并事件
图0.2 A∪BA∪B分成两两不相容的三个事件 - 乘法公式与条件概率
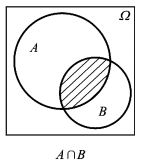
事件A,BA,B 同时发生的概率是:
P(A∩B)=P(A)P(B|A)=P(B)P(A|B)P(A∩B)=P(A)P(B|A)=P(B)P(A|B)
公式中的 P(A|B)P(A|B)是指在事件BB条件下事件AA发生的概率,又称作条件概率。
图0.3 两个事件的交事件 - 贝叶斯法则
由P(A∩B)=P(B|A)P(A)=P(A|B)P(B)P(A∪B)=P(B|A)P(A)=P(A|B)P(B)立得,
P(B|A)=P(A|B)P(B)P(A)P(B|A)=P(A|B)P(B)P(A)
在机器学习中我们通常写为:
P(h|D)=P(D|h)P(h)P(D)P(h|D)=P(D|h)P(h)P(D)
用P(h)P(h)表示在没有训练数据前假设hh拥有的初始概率。P(h)P(h)被称为h的先验概率。先验概率反映了关于h是一正确假设的机会的背景知识。
机器学习中,我们关心的是P(h|D)P(h|D),即给定D时h的成立的概率,称为h的后验概率。 - 全概率公式
设S是实验E的样本空间,B1,B2,...,BnB1,B2,...,Bn是E的n个两两不相容的时间,且有B1∪B2∪...∪Bn=SB1∪B2∪...∪Bn=S,也就是说S划分成n个两两不相容的时间:B1,B2,...,Bn.B1,B2,...,Bn.
又若A是实验E的任一事件,则有A=AS=A(B1∪B2∪...∪Bn)=AB1∪AB2∪...A∪BnA=AS=A(B1∪B2∪...∪Bn)=AB1∪AB2∪...A∪Bn
其中
这样就将A分成n个两两不相容的事件:AB1,AB2,...,ABn.AB1,AB2,...,ABn.设P(B_{i})>0(i=1,2,…,n),就有P(A)=∑i=1nP(ABi)=∑i=1nP(A|Bi)P(Bi)P(A)=∑i=1nP(ABi)=∑i=1nP(A|Bi)P(Bi)
我们称上述公式为全概率公式。
1. 贝叶斯决策论
有了第0节的基础概率知识之后,本节开始介绍贝叶斯决策论(Bayesian decision theory)。贝叶斯决策论是概率框架下实施决策的基本方法。
设有N 种可能的类别标记,即Y=c1,c2,...,cNY=c1,c2,...,cN,则基于后验概率P(ci|x)P(ci|x)可获得将样本x分类为cici所产生的期望损失(也称条件风险)为:
R(ci|x)=∑j=1NλijP(cj|x)(1.1)(1.1)R(ci|x)=∑j=1NλijP(cj|x)
其中λijλij是将一个真实标记为cjcj标记成为cici产生的损失.
我们的目的是寻找一个方法使得条件风险最小化。为最小化总体风险,只需在每个样本上选择哪个能是条件风险R(c|x)R(c|x)最小化的类别标记,即
h∗(x)=argminc∈YR(c|x)(1.2)(1.2)h∗(x)=argminc∈YR(c|x)
这就是贝叶斯判定准则(Bayes decision rule)。
若目标是最小化分类错误率,则条件风险为
R(c|x)=1−P(c|x)(1.3)(1.3)R(c|x)=1−P(c|x)
其中λijλij为0/1损失函数。
所以,最小化分类错误率的贝叶斯最优分类器为
h∗(x)=argmaxc∈YP(c|x)(1.4)(1.4)h∗(x)=argmaxc∈YP(c|x)
也就是对每个样本x,选择能使后验概率P(c|x)P(c|x)最大的类别标记。
通常情况下P(c|x)P(c|x)很难直接获得,根据我们已知的条件概率知识对公式1.4进行化简得
h∗(x)=argmaxc∈YP(c|x)=argmaxc∈YP(x|c)P(c)P(x)=argmaxc∈YP(x|c)P(c)(1.5)(1.5)h∗(x)=argmaxc∈YP(c|x)=argmaxc∈YP(x|c)P(c)P(x)=argmaxc∈YP(x|c)P(c)
其中P(c)为先验概率,P(x|c)P(x|c)为样本x关于类别c的条件概率。这就是后验概率最大化准则。这样一来,根据期望风险最小化原则就可以得到后验概率最大化准则。
在某些情况下,可假定Y中每个假设有相同的先验概率,这样式子1.5可以进一步简化为公式1.6,只需考虑P(x|c)来寻找极大可能假设。
h∗(x)=argmaxc∈YP(x|c)(1.6)(1.6)h∗(x)=argmaxc∈YP(x|c)
综合以上讨论,当前求最小化分类错误率的问题转化成了求解先验概率P(c)和条件概率(也称似然概率)P(x|c)P(x|c)的估计问题。对于先验概率P(c)表达了样本空间中各类样本所占的比例,根据大数定理,当训练集包含充足的独立同分布样本时,P(c)可以通过各类样本出现的频率进行估计。整个问题就变成了求解条件概率P(x|c)P(x|c)的问题。
2. 极大似然估计
极大似然轨迹源自于频率学派,他们认为参数虽然未知,但却是客观存在的规定值,因此,可以通过优化似然函数等准则确定参数数值。本节使用极大似然估计对条件概率进行估计。
令DcDc表示训练集D中第c类样本组成的集合,假设这些样本是独立同分布的,则参数θθ(θθ是唯一确定条件概率P(x|c)P(x|c)的参数向量)对数据集DcDc的似然函数是
P(Dc|θ)=∏x∈DcP(x|θ)(2.1)(2.1)P(Dc|θ)=∏x∈DcP(x|θ)
对2.1求对数似然函数
L(θ)=logP(Dc|θ)=log∏x∈DcP(x|θ)=∑x∈DclogP(x|θ)(2.2)(2.2)L(θ)=logP(Dc|θ)=log∏x∈DcP(x|θ)=∑x∈DclogP(x|θ)
因此求得θθ的极大似然估计θ^θ^为
θ^=argmaxθL(θ)(2.3)(2.3)θ^=argmaxθL(θ)
使用极大似然估计方法估计参数虽然简单,但是其结果的准确性严重依赖于每个问题所假设的概率分布形式是否符合潜在的真实数据分布,可能会产生误导性的结果。
3. 朴素贝叶斯分类器
从前面的介绍可知,使用贝叶斯公式来估计后验概率最大的困难是难以从现有的训练样本中准确的估计出条件概率P(x|c)P(x|c)的概率分布。朴素贝叶斯分类器为了避开这个障碍,朴素贝叶斯方法对条件概率分布作了条件独立性的假设。具体地,条件独立性假设是
P(x|c)=∏i=1dP(xi|c)(3.1)(3.1)P(x|c)=∏i=1dP(xi|c)
有了条件概率的简化条件之后,我们很容易将公式1.5的贝叶斯准则改写为
h∗(x)=argmaxc∈YP(c|x)=argmaxc∈YP(c)∏i=1dP(xi|c)(3.2)(3.2)h∗(x)=argmaxc∈YP(c|x)=argmaxc∈YP(c)∏i=1dP(xi|c)
公式3.2就是著名的朴素贝叶斯的表达式。
下面对先验概率P(c)和条件概率P(xi|c)P(xi|c)进行极大似然估计求得后验概率。
令DcDc表示训练集D中第c类样本组成的集合,先验概率的似然估计为
P(c)=|Dc||D|(3.3)(3.3)P(c)=|Dc||D|
对于离散属性而言,令Dc,xiDc,xi表示DcDc中在第i个属性上取值为xixi的样本组成的集合,则条件概率P(x|c)P(x|c)的似然估计为
P(x|c)=|Dc,xi||Dc|(3.4)(3.4)P(x|c)=|Dc,xi||Dc|
而对于连输属性需要考虑其密度函数。
朴素贝叶斯分类算法主要分成如下三步:
- 计算先验概率P(c)和条件概率P(x|c)
- 计算后验概率P(c|x)=P(c)∏di=1P(xi|c)P(c|x)=P(c)∏i=1dP(xi|c)
- 确定实例x的类h∗(x)=argmaxc∈YP(c)∏di=1P(xi|c)h∗(x)=argmaxc∈YP(c)∏i=1dP(xi|c)
拉普拉斯平滑:使用极大似然估计可能会出现所要估计的概率值为0的情况,这样会影响到后验概率的结果,最终使得推荐分类产生偏差。使用贝叶斯估计而已解决这一问题。具体地,条件概率的贝叶斯估计是
Pλ(x|c)=|Dc|+λ|Dc|+Nc∗λ(3.5)(3.5)Pλ(x|c)=|Dc|+λ|Dc|+Nc∗λ
当λ=1λ=1时称为拉普拉斯平滑(Laplace smoothing)。
同样先验概率的贝叶斯轨迹为
Pλ(c)=|Dc,xi|+λ|D|+N∗λ(3.6)(3.6)Pλ(c)=|Dc,xi|+λ|D|+N∗λ
显然,拉普拉斯平滑修正了因训练集样本不充分造成的概率为0的问题,并且在训练集变大时,估计值也逐渐趋向于实际的概率值。
4. 半朴素贝叶斯分类器
在现实任务中朴素贝叶斯的假设条件(属性条件独立)往往不成立,因此,在评估实际问题时朴素贝叶斯方法往往失去了部分精度,所以人们尝试对属性的独立性进行一定程度的放松,由此产生了半朴素贝叶斯分类器的学习方法。
半朴素贝叶斯分类器的基本思想是适当考虑一部分属性之间的相互依赖关系,从而既不需要完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
独立依赖估计是半朴素贝叶斯分类器最常用的一种策略,也就是假设每个属性在类别之 外最多依赖于一个 其他属性,即
P(c|x)∝P(c)∏i=1dP(xi|c,pai)(4.1)(4.1)P(c|x)∝P(c)∏i=1dP(xi|c,pai)
其中paipai为xixi所依赖的属性,称为xixi的父属性。由于作者对半朴素贝叶斯的理解有限,下面就简单的介绍几种常见的半朴素贝叶斯分类器,对于细节不再进行展开,如果想了解更多半朴素贝叶斯分类器的朋友可以参考书籍[1]。图4.1给出了朴素贝叶斯属性间的依赖关系(图4.1(a))、SPODE属性间的依赖关系(图4.1(b))和TAN属性间的依赖关系(图4.1(c))。 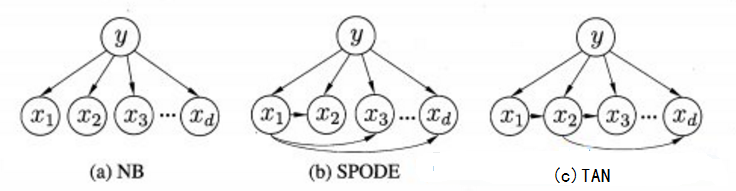
图4.1 属性依赖关系(图片来源于[1])
- SPODE(Super-Parent ODE)(超父独依赖估计):该方法假设所有属性都依赖于同一个属性,该属性被称为超父属性,如图4.1(b)所示x1x1是超父属性。
- TAN(Tree Augmented naive Bayes):该方法是在最大权生成树的基础上,首先通过计算两两属性之间的条件信息求出各个边的权值,然后构建完全图的最大带权生成树,最后加入类别y,增加从y到每个属性的有向边。如图4.1(c)所示为TAN属性的依赖关系。
参考文献
[1]: 周志华. 《机器学习》[M]. 清华大学出版社, 2016.
[2]: 李航. 《统计学习方法》[M].清华大学出版社,2013.
[3]: Tom M Michele. 《机器学习》[M].机械工业出版社,2003.







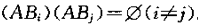













 3257
3257











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








