非线性方程求根及python实现
1. 非线性方程
- 考虑单变量非线性方程
f ( x ) = 0 \qquad\qquad f(x)=0\qquad f(x)=0其中, x ∈ R , f ( x ) ∈ C [ a , b ] x\in R,\ f(x)\in C[a,b] x∈R, f(x)∈C[a,b]
\qquad
显然,满足
f
(
x
∗
)
=
0
f(x^{\ast})=0
f(x∗)=0 的
x
∗
x^{\ast}
x∗ 即为方程的根。由于
x
x
x 的取值范围不同,求得的解也不同,讨论线性方程组的求解时,必须强调求解区间。
\qquad
- 如果非线性方程 f ( x ) f(x) f(x) 可以分解为:
f ( x ) = ( x − x ∗ ) m g ( x ) \qquad\qquad f(x)=(x-x^{\ast})^mg(x) f(x)=(x−x∗)mg(x)
\qquad
若
g
(
x
∗
)
≠
0
g(x^{\ast})\neq 0
g(x∗)=0,那么
x
∗
x^{\ast}
x∗ 为
f
(
x
)
f(x)
f(x) 的
m
m
m 重根。
\qquad
- 非线性方程的求解一般没有直接的公式,通常使用“迭代的方式”求解。
\qquad
2. 有根区间、二分法
2.1 有根区间
\qquad 迭代法需要给出根 x ∗ x^{\ast} x∗ 的一个初始值。
\qquad 若 f ( x ) ∈ C [ a , b ] f(x)\in C[a,b] f(x)∈C[a,b],且 f ( a ) f ( b ) < 0 f(a)f(b)<0 f(a)f(b)<0,有连续函数性质可知 f ( x ) = 0 f(x)=0 f(x)=0 在区间 ( a , b ) (a,b) (a,b) 内至少有一个实根,此时就称区间 [ a , b ] [a,b] [a,b] 为方程 f ( x ) = 0 f(x)=0 f(x)=0 的有根区间。
\qquad
有根区间可通过逐点搜索的方式得到。
\qquad
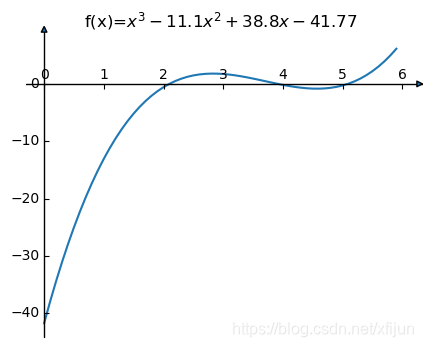
例
1
\textbf{例 1}
例 1 求方程
f
(
x
)
=
x
3
−
11.1
x
2
+
38.8
x
−
41.77
f(x)=x^3-11.1x^2 + 38.8x - 41.77
f(x)=x3−11.1x2+38.8x−41.77 在
[
0
,
6
]
[0,6]
[0,6] 内的有根区间。
import numpy as np
import matplotlib.pyplot as plt
def getInterval(f,a,b,h):
x = np.arange(a,b+h,h)
pts = []
xk = a
for i in range(1,len(x)):
if f(xk)*f(x[i]) < 0:
xk = x[i]
pts.append(xk-h)
pts.append(xk)
return np.array(pts)
if __name__ == '__main__':
fig = plt.figure
f = lambda x: x**3 - 11.1*x**2 + 38.8*x - 41.77
a = 0.0
b = 6.0
intpts = getInterval(f,a,b,0.2) # 搜索步长为0.2
print(intpts)
x = np.arange(0,6,0.1)
plt.plot(x,f(x))
plt.title('f(x)')
plt.show()
计算结果:
[2. 2.2 3.8 4. 5. 5.2] 搜索步长为0.2
[2. 2.4 3.6 4. 4.8 5.2] 搜索步长为0.4
[1.8 2.4 3.6 4.2 4.8 5.4] 搜索步长为0.6
[1.6 2.4 3.2 4. 4.8 5.6] 搜索步长为0.8
[2. 3. 3. 4. 5. 6. ] 搜索步长为1
\qquad
\qquad
在有根区间上求解方程
f
(
x
)
=
0
f(x)=0
f(x)=0 可采用二分法。
\qquad
2.2 二分法
\qquad
假设在有根区间
[
a
,
b
]
[a,b]
[a,b] 只有一个根,取中点
x
0
=
a
+
b
2
x_0=\frac{a+b}{2}
x0=2a+b 将其分为两半。若
x
0
x_0
x0 不是
f
(
x
)
f(x)
f(x) 的零点,就可以进行根的搜索:
(
1
)
\qquad(1)
(1) 若
f
(
x
0
)
f
(
a
)
>
0
f(x_0)f(a)>0
f(x0)f(a)>0,那么有根区间
[
a
,
b
]
[a,b]
[a,b] 缩小为
[
x
0
,
b
]
[x_0,b]
[x0,b]
(
2
)
\qquad(2)
(2) 若
f
(
x
0
)
f
(
b
)
>
0
f(x_0)f(b)>0
f(x0)f(b)>0,那么有根区间
[
a
,
b
]
[a,b]
[a,b] 缩小为
[
a
,
x
0
]
[a,x_0]
[a,x0]
\qquad 显然,将有根区间二分之后,“新有根区间”长度为“原有根区间”长度的一半。一直二分下去,可以得到一系列的有根区间:
[ a , b ] ⊃ [ a 1 , b 1 ] ⊃ [ a 2 , b 2 ] ⊃ ⋯ ⊃ [ a k , b k ] ⊃ ⋯ \qquad\qquad[a,b]\supset[a_1,b_1]\supset[a_2,b_2]\supset\cdots\supset[a_k,b_k]\supset\cdots [a,b]⊃[a1,b1]⊃[a2,b2]⊃⋯⊃[ak,bk]⊃⋯
\qquad
每次二分之后,取有根区间
[
a
k
,
b
k
]
[a_k,b_k]
[ak,bk] 的中点
x
k
=
a
k
+
b
k
2
x_k=\dfrac{a_k+b_k}{2}
xk=2ak+bk 作为根的近似值。因此,二分过程中实际上是得到了一个近似跟的序列
x
0
,
x
1
,
⋯
,
x
k
,
⋯
x_0,x_1,\cdots,x_k,\cdots
x0,x1,⋯,xk,⋯,该序列必以根
x
∗
x^{\ast}
x∗ 为极限。
\qquad
\qquad
二分区间序列的长度满足:
b
k
−
a
k
=
b
−
a
2
k
b_k-a_k=\dfrac{b-a}{2^k}
bk−ak=2kb−a,二分次数取决于运算精度要求:
∣
x
∗
−
x
k
∣
<
ε
\vert x^{\ast}-x_k\vert<\varepsilon
∣x∗−xk∣<ε。
\qquad
二分法步骤
令 k = 0 k=0 k=0,有根区间 [ a 0 , b 0 ] = [ a , b ] [a_0,b_0]=[a,b] [a0,b0]=[a,b]
步骤 1 : 1: 1: 计算有根区间 [ a k , b k ] = [ a , b ] [a_k,b_k]=[a,b] [ak,bk]=[a,b] 的端点函数值 f ( a k ) , f ( b k ) f(a_k),f(b_k) f(ak),f(bk)
步骤 2 : 2: 2: 计算区间中点 x k = a k + b k 2 x_k=\dfrac{a_k+b_k}{2} xk=2ak+bk 处的函数值 f ( x k ) f(x_k) f(xk)
步骤
3
:
3:
3: 若
f
(
x
k
)
=
0
f(x_k)=0
f(xk)=0,则根为
x
∗
=
x
k
x^{\ast}=x_k
x∗=xk;
\qquad
若
f
(
a
k
)
f
(
x
k
)
<
0
f(a_k)f(x_k)<0
f(ak)f(xk)<0,那么
a
k
+
1
=
a
k
,
b
k
+
1
=
x
k
a_{k+1}=a_k,\ b_{k+1}=x_k
ak+1=ak, bk+1=xk;
\qquad
否则,
a
k
+
1
=
x
k
,
b
k
+
1
=
b
k
a_{k+1}=x_k,\ b_{k+1}=b_k
ak+1=xk, bk+1=bk
重复执行步骤 1 ∼ 3 1\sim3 1∼3,直到 ∣ a k − b k ∣ < ε \vert a_k-b_k\vert<\varepsilon ∣ak−bk∣<ε, x ∗ = x k = a k + b k 2 x^{\ast}=x_k=\dfrac{a_k+b_k}{2} x∗=xk=2ak+bk
\qquad
例
2
\textbf{例 2}
例 2 求方程
f
(
x
)
=
x
3
−
11.1
x
2
+
38.8
x
−
41.77
f(x)=x^3-11.1x^2 + 38.8x - 41.77
f(x)=x3−11.1x2+38.8x−41.77 在
[
0
,
6
]
[0,6]
[0,6] 内的根。
import numpy as np
def getInterval(f,a,b,h):
(见2.1节,略)
def bisection(f,a,b,eps): #二分法:在有根区间[a,b]求解
ta = a
tb = b
flag = 1
n = 1
while flag:
tc = (ta+tb)/2
# print('a%d: %.4f | b%d: %.4f | c%d: %.4f | f(xk): %.4f'\
# % (n,ta,n,tb,n,tc,f(tc)))
if f(tc)*f(ta)<0:
tb = tc
elif f(tc)*f(tb)<0:
ta = tc
else: #if f(tc)==0:
val = tc
n += 1
if np.abs(ta-tb)<eps:
val = tc
flag = 0
return val
if __name__ == '__main__':
f = lambda x: x**3 - 11.1*x**2 + 38.8*x - 41.77
a = 0.0
b = 6.0
for h in [0.2,0.4,0.6,1]:
pts = getInterval(f,a,b,h)
print(pts)
for i in range(0,len(pts),2):
val = bisection(f,pts[i],pts[i+1],0.0001)
print('bisection:',val)
计算结果:
[2. 2.2 3.8 4. 5. 5.2] (step = 0.2)
bisection [2.0, 2.2]: 2.09638671875
bisection [3.8, 4.0]: 3.91767578125
bisection [5.0, 5.2]: 5.08583984375
[2. 2.4 3.6 4. 4.8 5.2] (step = 0.4)
bisection [2.0, 2.4]: 2.0963867187500007
bisection [3.6, 4.0]: 3.91767578125
bisection [4.8, 5.2]: 5.08583984375
[1.8 2.4 3.6 4.2 4.8 5.4] (step = 0.6)
bisection [1.8, 2.4]: 2.096264648437499
bisection [3.6, 4.2]: 3.9177978515625007
bisection [4.8, 5.4]: 5.0858642578125
[1.6 2.4 3.2 4. 4.8 5.6] (step = 0.8)
bisection [1.6, 2.4]: 2.0963867187500007
bisection [3.2, 4.0]: 3.91767578125
bisection [4.8, 5.6]: 5.085839843750001
[2. 3. 3. 4. 5. 6.] (step = 1.0)
bisection [2.0, 3.0]: 2.09637451171875
bisection [3.0, 4.0]: 3.91778564453125
bisection [5.0, 6.0]: 5.08587646484375
\qquad
3. 不动点迭代法
\qquad 将方程 f ( x ) = 0 f(x)=0 f(x)=0 改写成等价的形式: x = φ ( x ) x=\varphi(x) x=φ(x) 。由于方程的根 x ∗ x^{\ast} x∗ 满足 f ( x ∗ ) = 0 f(x^{\ast})=0 f(x∗)=0,必然也满足 x ∗ = φ ( x ∗ ) x^{\ast}=\varphi(x^{\ast}) x∗=φ(x∗),此时称根 x ∗ x^{\ast} x∗ 为函数 φ ( x ) \varphi(x) φ(x) 的一个不动点。
\qquad
\qquad
因此,求
f
(
x
)
=
0
f(x)=0
f(x)=0 就相当于求
φ
(
x
)
\varphi(x)
φ(x) 的不动点,也就是不动点迭代法:
(
1
)
\qquad(1)
(1) 令
k
=
0
k=0
k=0,选择初始值
x
0
x_0
x0
(
2
)
\qquad(2)
(2) 根据
x
k
x_k
xk 的值,可求得
x
k
+
1
=
φ
(
x
k
)
x_{k+1}=\varphi(x_k)
xk+1=φ(xk)
\qquad
此时,称函数
φ
(
x
)
\varphi(x)
φ(x) 为迭代函数。如果
∀
x
0
∈
[
a
,
b
]
\forall\ x_0\in[a,b]
∀ x0∈[a,b],由迭代方程
x
k
+
1
=
φ
(
x
k
)
x_{k+1}=\varphi(x_k)
xk+1=φ(xk) 得到的序列
{
x
k
}
k
=
0
∞
\{x_k\}_{k=0}^{\infty}
{xk}k=0∞ 有极限,即:
lim
x
→
∞
x
k
=
x
∗
\displaystyle\lim_{\scriptscriptstyle x\rightarrow\infty}x_k=x^{\ast}
x→∞limxk=x∗,则称迭代方程
x
k
+
1
=
φ
(
x
k
)
x_{k+1}=\varphi(x_k)
xk+1=φ(xk) 收敛,
x
∗
x^{\ast}
x∗ 为
φ
(
x
)
\varphi(x)
φ(x) 的不动点。
\qquad
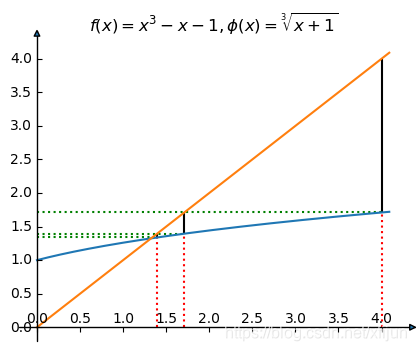
例 3 3 3 中使用不动点迭代法示意图(为方便显示,初始点为 x 0 = 4 x_0=4 x0=4,精度要求设为 eps = 0.1 \text{eps}=0.1 eps=0.1)
\qquad “不动点迭代法”的基本思想,是将方程 f ( x ) = 0 f(x)=0 f(x)=0 写成等价的隐式方程 x = φ ( x ) x=\varphi(x) x=φ(x),用逐次逼近的方式来求不动点,也就是方程 f ( x ) = 0 f(x)=0 f(x)=0 的解。
\qquad
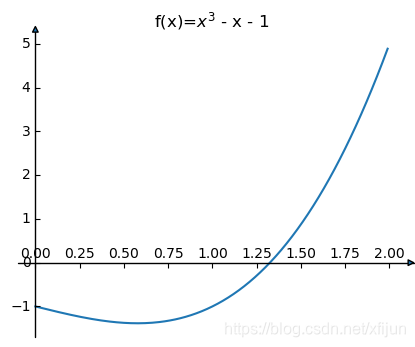
例 3 \textbf{例 3} 例 3 求方程 f ( x ) = x 3 − x − 1 f(x)=x^3-x-1 f(x)=x3−x−1 在 x 0 = 1.5 x_0=1.5 x0=1.5 附近的根。
构造隐式方程: f ( x ) = x 3 − x − 1 = 0 ⟶ x = ( x + 1 ) 3 f(x)=x^3-x-1=0\newline\qquad\qquad\quad\qquad\longrightarrow\quad x=\sqrt[3]{(x+1)} f(x)=x3−x−1=0⟶x=3(x+1)
此时的迭代函数: φ ( x ) = ( x + 1 ) 3 \varphi(x)=\sqrt[3]{(x+1)} φ(x)=3(x+1)
迭代公式为: x k + 1 = ( x k + 1 ) 3 x_{k+1}=\sqrt[3]{(x_k+1)} xk+1=3(xk+1)
import numpy as np
def fixedpoint(f,phi,x0,eps):
xk0 = x0
flag = 1
n = 1
while flag:
xk1 = phi(xk0)
print('#%d: xk=%.5f, f(xk)=%.5f'%(n,xk1,f(xk1)))
if np.abs(xk1-xk0)<eps or n>10:
val = (xk1+xk0)/2
flag = 0
xk0 = xk1
n += 1
return val
if __name__ == '__main__':
f = lambda x: x**3 - x - 1
phi = lambda x: (x+1)**(1/3)
eps = 0.00001
val = fixedpoint(f,phi,1.5,eps) # 初始值为1.5
print('fixed point:',val)
计算结果:
#1: x1=1.35721, f(x1)=0.142791
#2: x2=1.33086, f(x2)=0.026348
#3: x3=1.32588, f(x3)=0.004977
#4: x4=1.32494, f(x4)=0.000944
#5: x5=1.32476, f(x5)=0.000179
#6: x6=1.32473, f(x6)=0.000034
#7: x7=1.32472, f(x7)=0.000006
fixed point: 1.324719474534364
\qquad
值得注意的是:不动点迭代法并不总是能够收敛,主要取决于迭代方程的构造,或者说迭代函数的选择。
\qquad
反例
\textbf{反例}
反例在上例中,如果构造隐式方程:
f
(
x
)
=
x
3
−
x
−
1
=
0
⟶
x
=
x
3
−
1
f(x)=x^3-x-1=0\newline\qquad\qquad\qquad\qquad \qquad\qquad \qquad\qquad\longrightarrow\quad x=x^3-1
f(x)=x3−x−1=0⟶x=x3−1
此时的迭代函数: φ ( x ) = x 3 − 1 \varphi(x)=x^3-1 φ(x)=x3−1,迭代公式为: x k + 1 = x k 3 − 1 x_{k+1}=x_k^3-1 xk+1=xk3−1
此时,采用不动点迭代法是发散的。
\qquad
4. 迭代法的加速方法
\qquad 对于收敛的迭代过程,迭代足够多次都可以达到所需的精度要求。然而,如果迭代过程收敛比较缓慢,就会增大求根过程的计算量。
4.1 埃特金(Aitken)加速
\qquad 设 x 0 x_0 x0 是根 x ∗ x^{\ast} x∗ 的某个近似解,假设迭代函数为 φ ( x ) \varphi(x) φ(x),显然有:
{ x 1 = φ ( x 0 ) x ∗ = φ ( x ∗ ) \qquad\qquad\left\{\begin{aligned}x_1=\varphi(x_0)\\x^{\ast}=\varphi(x^{\ast})\end{aligned}\right. {x1=φ(x0)x∗=φ(x∗)
( 1 ) \qquad(1) (1) 由微分中值定理,可得到
x 1 − x ∗ = φ ( x 0 ) − φ ( x ∗ ) = φ ′ ( ξ ) ( x 0 − x ∗ ) \qquad\qquad x_1-x^{\ast}=\varphi(x_0)-\varphi(x^{\ast})=\varphi^{'}(\xi)(x_0-x^{\ast}) x1−x∗=φ(x0)−φ(x∗)=φ′(ξ)(x0−x∗)
(
2
)
\qquad(2)
(2) 假设
φ
′
(
ξ
)
\varphi^{'}(\xi)
φ′(ξ) 的值变化不大,可以近似地取某个值
φ
′
(
ξ
)
≈
L
\varphi^{'}(\xi)\approx L
φ′(ξ)≈L,那么
x
1
−
x
∗
≈
L
(
x
0
−
x
∗
)
\qquad\qquad x_1-x^{\ast}\approx L(x_0-x^{\ast})
x1−x∗≈L(x0−x∗)
\qquad
继续迭代一次,就有
x
2
=
φ
(
x
1
)
x_2=\varphi(x_1)
x2=φ(x1),同样采用上述思路,可以得到
x
2
−
x
∗
=
φ
(
x
1
)
−
φ
(
x
∗
)
=
φ
′
(
ξ
)
(
x
1
−
x
∗
)
≈
L
(
x
1
−
x
∗
)
\qquad\qquad\begin{aligned} x_2-x^{\ast}&=\varphi(x_1)-\varphi(x^{\ast})=\varphi^{'}(\xi)(x_1-x^{\ast})\\ &\approx L(x_1-x^{\ast})\end{aligned}
x2−x∗=φ(x1)−φ(x∗)=φ′(ξ)(x1−x∗)≈L(x1−x∗)
\qquad 将两式联立,消去未知数 L L L,可得到:
x 1 − x ∗ x 2 − x ∗ ≈ x 0 − x ∗ x 1 − x ∗ \qquad\qquad\dfrac{x_1-x^{\ast}}{x_2-x^{\ast}}\approx\dfrac{x_0-x^{\ast}}{x_1-x^{\ast}} x2−x∗x1−x∗≈x1−x∗x0−x∗ ⟹ \quad\Longrightarrow ⟹ x ∗ ≈ x 0 − ( x 1 − x 0 ) 2 x 2 − 2 x 1 + x 0 \quad x^{\ast}\approx x_0-\dfrac{(x_1-x_0)^2}{x_2-2x_1+x_0} x∗≈x0−x2−2x1+x0(x1−x0)2
从该公式可以看出,在得到了 x 0 , x 1 , x 2 x_0,x_1,x_2 x0,x1,x2 之后,就可以求出新一轮 x ∗ x^{\ast} x∗ 的近似值,并记为 y 1 = x ∗ y_1=x^{\ast} y1=x∗。
\qquad 因此,埃特金 (Aitken) \text{(Aitken)} (Aitken) 加速的公式可以表示为:
y k + 1 ≈ x k − ( x k + 1 − x k ) 2 x k + 2 − 2 x k + 1 + x k \qquad\qquad y_{k+1}\approx x_k-\dfrac{(x_{k+1}-x_k)^2}{x_{k+2}-2x_{k+1}+x_k} yk+1≈xk−xk+2−2xk+1+xk(xk+1−xk)2
若将加速公式写为 y k + 1 ≈ x k − ( x k + 1 − x k ) 2 x k + 2 − 2 x k + 1 + x k = x k − ( Δ x k ) 2 Δ 2 x k y_{k+1}\approx x_k-\dfrac{(x_{k+1}-x_k)^2}{x_{k+2}-2x_{k+1}+x_k}=x_k-\dfrac{(\Delta x_k)^2}{\Delta^2 x_k} yk+1≈xk−xk+2−2xk+1+xk(xk+1−xk)2=xk−Δ2xk(Δxk)2
相当于定义了迭代函数 ψ ( x ) = x − ( Δ x ) 2 Δ 2 x \psi(x)=x-\dfrac{(\Delta x)^2}{\Delta^2 x} ψ(x)=x−Δ2x(Δx)2,以及迭代方程 y k + 1 = ψ ( x k ) y_{k+1}=\psi(x_k) yk+1=ψ(xk)
\qquad 可以证明,由埃特金加速方法产生的序列 { y k } \{y_k\} {yk} 比 { x k } \{x_k\} {xk} 更快收敛到 x ∗ x^{\ast} x∗。
\qquad
例
4
\textbf{例 4}
例 4求方程
f
(
x
)
=
x
3
−
x
−
1
f(x)=x^3-x-1
f(x)=x3−x−1 在
x
0
=
1.5
x_0=1.5
x0=1.5 附近的根。
构造隐式方程: f ( x ) = x 3 − x − 1 = 0 ⟶ x = ( x + 1 ) 3 f(x)=x^3-x-1=0\newline\qquad\qquad\quad\qquad\longrightarrow\quad x=\sqrt[3]{(x+1)} f(x)=x3−x−1=0⟶x=3(x+1)
迭代函数: φ ( x ) = ( x + 1 ) 3 \varphi(x)=\sqrt[3]{(x+1)} φ(x)=3(x+1)
迭代公式为: y k + 1 = ψ ( x k ) = x k − ( x k + 1 − x k ) 2 x k + 2 − 2 x k + 1 + x k y_{k+1}=\psi(x_k)=x_k-\dfrac{(x_{k+1}-x_k)^2}{x_{k+2}-2x_{k+1}+x_k} yk+1=ψ(xk)=xk−xk+2−2xk+1+xk(xk+1−xk)2
import numpy as np
def aitken(f,phi,x,eps):
xk0 = x
yk0 = xk0
flag = 1
n = 1
while flag:
xk1 = phi(xk0)
xk2 = phi(xk1)
yk1 = xk0 - (xk1-xk0)**2/(xk2-2*xk1+xk0)
print('#%d: yk=%.5f, f(yk)=%f'%(n,yk1,f(yk1)))
if np.abs(yk1-yk0)<eps:
val = yk1
flag = 0
yk0 = yk1
xk0 = xk1
xk1 = xk2
n += 1
return val
if __name__ == '__main__':
f = lambda x: x**3 - x - 1 # 例4
phi = lambda x: (x+1)**(1/3)
eps = 0.00001
val = aitken(f,phi,1.5,eps)
print('aitken:',val)
计算结果:
#1: y1=1.32490, f(y1)=0.000773
#2: y2=1.32472, f(y2)=0.000028
#3: y3=1.32472, f(y3)=0.000001
aitken: 1.32471819755562
对比例
3
3
3 结果,不动点迭代法需要
7
7
7 次才能达到
6
6
6 位有效数字,而埃特金加速方法只需要
2
2
2 次迭代。
\qquad
4.2 斯特芬森(Steffensen)加速
\qquad 斯特芬森 (Steffensen) \text{(Steffensen)} (Steffensen)加速法,是将“埃特金加速方法”与“不动点迭代法”相结合的过程。
\qquad 假设不动点迭代法采用的迭代函数为 φ ( x ) \varphi(x) φ(x),令:
{ y k = x k + 1 = φ ( x k ) z k = φ ( y k ) = φ ( x k + 1 ) = x k + 2 \qquad\qquad\left\{\begin{aligned}y_k&=x_{k+1}=\varphi(x_k) \\ \\z_k&=\varphi(y_k)=\varphi(x_{k+1})=x_{k+2}\end{aligned}\right. ⎩ ⎨ ⎧ykzk=xk+1=φ(xk)=φ(yk)=φ(xk+1)=xk+2
\qquad 埃特金加速公式就可以写为:
x k + 1 = x k − ( x k + 1 − x k ) 2 x k + 2 − 2 x k + 1 + x k = x k − ( y k − x k ) 2 z k − 2 y k + x k \qquad\qquad\begin{aligned}x_{k+1}&=x_k-\dfrac{(x_{k+1}-x_k)^2}{x_{k+2}-2x_{k+1}+x_k}\\ &=x_k-\dfrac{(y_k-x_k)^2}{z_k-2y_k+x_k}\end{aligned} xk+1=xk−xk+2−2xk+1+xk(xk+1−xk)2=xk−zk−2yk+xk(yk−xk)2
\qquad
将上式写成
x
k
+
1
=
ψ
(
x
k
)
x_{k+1}=\psi(x_k)
xk+1=ψ(xk) 的形式,相当于定义了新的迭代函数
ψ
(
x
)
\psi(x)
ψ(x),也就是
ψ
(
x
)
=
x
−
[
φ
(
x
)
−
x
]
2
φ
(
φ
(
x
)
)
−
2
φ
(
x
)
+
x
\qquad\qquad\psi(x)=x-\dfrac{\left[\varphi(x)-x\right]^2}{\varphi(\varphi(x))-2\varphi(x)+x}
ψ(x)=x−φ(φ(x))−2φ(x)+x[φ(x)−x]2
\qquad
\qquad
例
5
\textbf{例 5}
例 5 求方程
f
(
x
)
=
x
3
−
x
−
1
f(x)=x^3-x-1
f(x)=x3−x−1 在
x
0
=
1.5
x_0=1.5
x0=1.5 附近的根。
构造隐式方程: f ( x ) = x 3 − x − 1 = 0 ⟶ x = x 3 − 1 f(x)=x^3-x-1=0\newline\qquad\qquad\quad\qquad\longrightarrow\quad x=x^3-1 f(x)=x3−x−1=0⟶x=x3−1
此时的迭代函数: φ ( x ) = x 3 − 1 \varphi(x)=x^3-1 φ(x)=x3−1 【由例3可知,该迭代函数直接使用“不动点迭代法”是发散的】
迭代公式为:
x
k
+
1
=
x
k
3
−
1
x_{k+1}=x_k^3-1
xk+1=xk3−1
\qquad
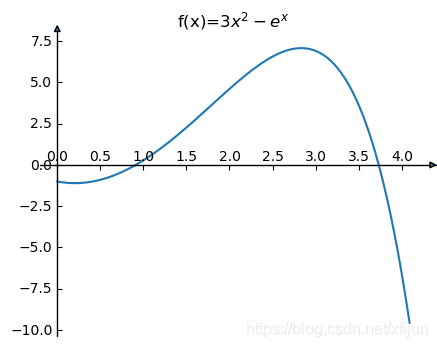
例
6
\textbf{例 6}
例 6 求方程
f
(
x
)
=
3
x
2
−
e
x
f(x)=3x^2-e^x
f(x)=3x2−ex 在
[
3
,
4
]
[3,4]
[3,4] 中的解。
构造隐式方程: f ( x ) = 3 x 2 − e x = 0 ⟶ x = ln 3 x 2 f(x)=3x^2-e^x=0\newline\qquad\qquad\quad\qquad\longrightarrow\quad x=\ln3x^2 f(x)=3x2−ex=0⟶x=ln3x2
此时的迭代函数: φ ( x ) = ln 3 x 2 = 2 ln x + ln 3 \varphi(x)=\ln3x^2=2\ln x+\ln3 φ(x)=ln3x2=2lnx+ln3
迭代公式为: x k + 1 = 2 ln x k + ln 3 x_{k+1}=2\ln x_k+\ln3 xk+1=2lnxk+ln3
import numpy as np
def steffensen(f,phi,x,eps):
xk = x
flag = 1
n = 1
while flag:
yk = phi(xk)
zk = phi(yk)
xk1 = xk - (yk-xk)**2/(zk-2*yk+xk)
print('#%d: xk=%.5f, f(xk)=%f'%(n,xk1,f(xk1)))
if np.abs(xk1-xk)<eps:
val = xk1
flag = 0
xk = xk1
n += 1
return val
if __name__ == '__main__':
f = lambda x: x**3 - x - 1 # 例5
phi = lambda x: x**3 - 1 # 即使迭代法不收敛,用斯蒂芬森法仍可能收敛
eps = 0.00001
val = steffensen(f,phi,1.5,eps) #初值为1.5
print('steffensen:',val)
f = lambda x: 3*x*x - np.exp(x) # 例6
phi = lambda x: 2*np.log(x)+np.log(3)
val = fixedpoint(f,phi,3.5,eps/2)
print('fixed point:',val)
val = steffensen(f,phi,3.5,eps) #初值为3.5
print('steffensen:',val)
计算结果:
例5中,使用不动点迭代法发散,使用steffensen加速法却可以收敛
#1: x1=1.50000, y1=2.37500, z1=12.39648, f(x1)=0.424629
#2: x2=1.41629, y2=1.84092, z2=5.23887, f(x2)=0.135748
#3: x3=1.35565, y3=1.49140, z3=2.31727, f(x3)=0.018114
#4: x4=1.32895, y4=1.34706, z4=1.44435, f(x4)=0.000369
#5: x5=1.32480, y5=1.32517, z5=1.32712, f(x5)=0.000000
#6: x6=1.32472, y6=1.32472, z6=1.32472, f(x6)=0.000000
steffensen: 1.3247179572447527
例6中,使用不动点迭代法(达到6位有效数字,需要迭代18次)
#1: x1=3.60414, f(x1)=2.219437
#2: x2=3.66278, f(x2)=1.278384
#3: x3=3.69506, f(x3)=0.712493
#4: x4=3.71260, f(x4)=0.389964
#5: x5=3.72208, f(x5)=0.211342
#6: x6=3.72718, f(x6)=0.113929
#7: x7=3.72991, f(x7)=0.061240
#8: x8=3.73138, f(x8)=0.032868
#9: x9=3.73217, f(x9)=0.017626
#10: x10=3.73259, f(x10)=0.009448
#11: x11=3.73282, f(x11)=0.005063
#12: x12=3.73294, f(x12)=0.002713
#13: x13=3.73300, f(x13)=0.001454
#14: x14=3.73304, f(x14)=0.000779
#15: x15=3.73306, f(x15)=0.000417
#16: x16=3.73307, f(x16)=0.000224
#17: x17=3.73307, f(x17)=0.000120
#18: x18=3.73308, f(x18)=0.000064
fixed point: 3.7330757227621447
例6中,使用steffensen加速(达到6位有效数字,只需要迭代3次)
#1: x1=3.50000, y1=3.60414, z1=3.66278, f(x1)=-0.102862
#2: x2=3.73835, y2=3.73590, z2=3.73459, f(x2)=-0.000045
#3: x3=3.73308, y3=3.73308, z3=3.73308, f(x3)=-0.000000
steffensen: 3.7330790286332505
\qquad
5. 牛顿法、 弦截法
1. 牛顿法 \textbf{1. 牛顿法} 1. 牛顿法
\qquad 牛顿法的基本思路是,将 f ( x ) f(x) f(x) 在 x k x_k xk 处进行一阶的泰勒级数近似。
f ( x ) ≈ f ( x k ) + f ′ ( x k ) ( x − x k ) \qquad\qquad f(x)\approx f(x_k)+f^{'}(x_k)(x-x_k) f(x)≈f(xk)+f′(xk)(x−xk)
\qquad 此时,方程 f ( x ) = 0 f(x)=0 f(x)=0 就可以表示为: f ( x k ) + f ′ ( x k ) ( x − x k ) = 0 f(x_k)+f^{'}(x_k)(x-x_k)=0 f(xk)+f′(xk)(x−xk)=0
\qquad
将求得的
x
x
x 值作为新迭代点
x
k
+
1
x_{k+1}
xk+1,也就得到了牛顿法的迭代公式:
x
k
+
1
=
x
k
−
f
(
x
k
)
f
′
(
x
k
)
\qquad\qquad x_{k+1}=x_k-\dfrac{f(x_k)}{f^{'}(x_k)}
xk+1=xk−f′(xk)f(xk)
可认为牛顿法的迭代函数为 φ ( x ) = x − f ( x ) f ′ ( x ) \varphi(x)=x-\dfrac{f(x)}{f^{'}(x)} φ(x)=x−f′(x)f(x)
\qquad
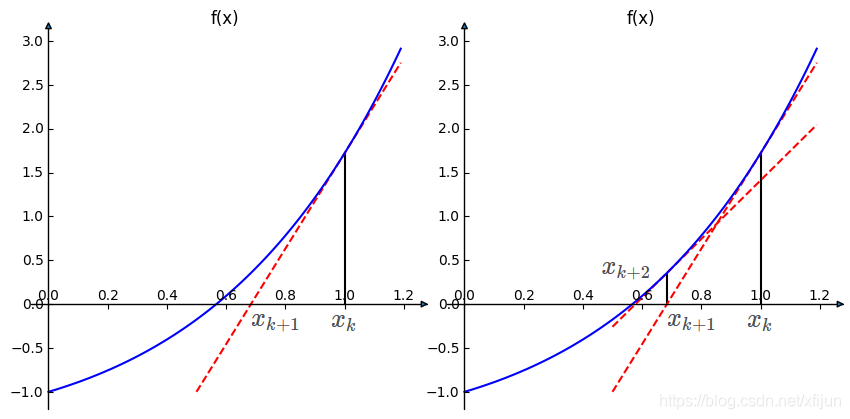
\qquad
从例
7
7
7 中函数求解的示意图可以看出,在点
x
k
=
1
x_k=1
xk=1 处用一阶泰勒级数(线性函数)近似
f
(
x
)
f(x)
f(x),将近似的直线与
x
x
x 轴相交的值,作为下一次迭代点
x
k
+
1
x_{k+1}
xk+1。在点
x
k
+
1
x_{k+1}
xk+1 处再次使用用一阶泰勒级数(线性函数)近似
f
(
x
)
f(x)
f(x),将近似的直线与
x
x
x 轴相交的值,作为下一次迭代点
x
k
+
2
x_{k+2}
xk+2。
\qquad
2.
简化牛顿法
\textbf{2. 简化牛顿法}
2. 简化牛顿法
\qquad
牛顿法的一种简化版本,称为“简化牛顿法”或者“平行弦法”。在牛顿法的迭代公式中,用初始点
x
0
x_0
x0 的微分值代替所有后续迭代点,也就是:
x
k
+
1
=
x
k
−
f
(
x
k
)
f
′
(
x
0
)
\qquad\qquad x_{k+1}=x_k-\dfrac{f(x_k)}{f^{'}(x_0)}
xk+1=xk−f′(x0)f(xk)
\qquad
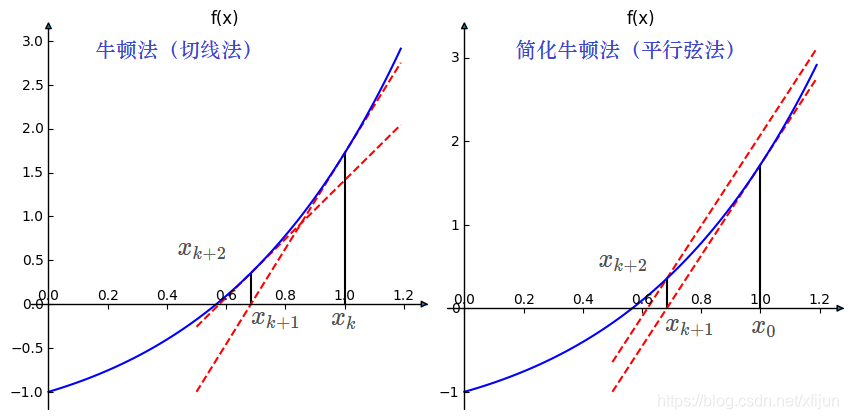
牛顿法的迭代点,是过每个 ( x k , f ( x k ) ) (x_k,f(x_k)) (xk,f(xk)) 点做切线与 x x x 轴的交点形成的
简化牛顿法只在 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0)) 点做切线,其他迭代点的斜率都使用 f ′ ( x 0 ) f^{'}(x_0) f′(x0),迭代点是一系列平行线与 x x x 轴的交点
\qquad
3.
弦截法
\textbf{3. 弦截法}
3. 弦截法
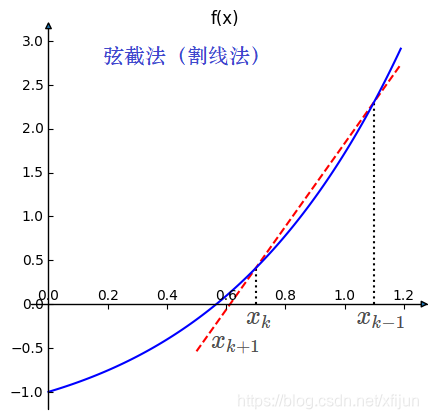
\qquad 弦截法需要用到 2 2 2 个初始点 x k − 1 x_{k-1} xk−1 和 x k x_{k} xk,通过做出一条通过点 ( x k − 1 , f ( x k − 1 ) ) (x_{k-1},f(x_{k-1})) (xk−1,f(xk−1)) 和点 ( x k , f ( x k ) ) (x_{k},f(x_{k})) (xk,f(xk)) 的直线:
y = f ( x k ) + f ( x k ) − f ( x k − 1 ) x k − x k − 1 ( x − x k ) \qquad\qquad y=f(x_k)+\dfrac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}(x-x_k) y=f(xk)+xk−xk−1f(xk)−f(xk−1)(x−xk)
\qquad
将该直线与
x
x
x 轴的交点作为下一个迭代点
x
k
+
1
x_{k+1}
xk+1,也称为“割线法”。
\qquad
\qquad
弦截法的迭代公式为:
x
k
+
1
=
x
k
−
f
(
x
k
)
f
(
x
k
)
−
f
(
x
k
−
1
)
(
x
k
−
x
k
−
1
)
\qquad\qquad x_{k+1}=x_k-\dfrac{f(x_k)}{f(x_k)-f(x_{k-1})}(x_k-x_{k-1})
xk+1=xk−f(xk)−f(xk−1)f(xk)(xk−xk−1)
\qquad 与牛顿法相比,弦截法不需要求函数的微分,但是每次计算需要用到两个初始点。
\qquad
例
7
\textbf{例 7}
例 7 求方程
f
(
x
)
=
x
e
x
−
1
f(x)=xe^x-1
f(x)=xex−1 在
x
0
=
0.5
x_0=0.5
x0=0.5 附近的解。
import numpy as np
def diff1_c(f,x,h):
return (f(x+h)-f(x-h))/(2*h)
def newton(f,x0,eps):
xk = x0
flag = 1
n = 1
while flag:
xk1 = xk - f(xk)/diff1_c(f,xk,0.001)
print('#%d: x%d=%.5f, f(x%d)=%.5f'%(n,n,xk1,n,f(xk1)))
if np.abs(xk1-xk)<eps:
val = xk1
flag = 0
xk = xk1
n += 1
return val
def simplifiednewton(f,x0,eps):
xk = x0
cx = diff1_c(f,x0,0.001)
flag = 1
n = 1
while flag:
xk1 = xk - f(xk)/cx
print('#%d: x%d=%.5f, f(x%d)=%.5f'%(n,n,xk1,n,f(xk1)))
if np.abs(xk1-xk)<eps:
val = xk1
flag = 0
xk = xk1
n += 1
return val
def secant(f,x0,x1,eps):
flag = 1
if f(x0) < f(x1):
xk0 = x1
xk1 = x0
else:
xk0 = x0
xk1 = x1
n = 1
while flag:
xk2 = xk1 - f(xk1)*(xk1-xk0)/(f(xk1)-f(xk0))
print('#%d: x%d=%.5f, f(x%d)=%.5f'%(n,n,xk2,n,f(xk2)))
if np.abs(xk2-xk1)<eps:
val = xk2
flag = 0
xk0 = xk1
xk1 = xk2
n += 1
return val
if __name__ == '__main__':
eps = 0.0001
f = lambda x: x*np.exp(x) - 1
val = newton(f,0.8,eps) ## newton
print('newton:',val)
val = simplifiednewton(f,0.8,eps/100) ## simplified newton
print('simplified newton:',val)
val = secant(f,0.7,1.1,eps) ## secant
print('secant:',val)
计算结果:
#1: x1=0.60518, f(x1)=0.10845
#2: x2=0.56830, f(x2)=0.00319
#3: x3=0.56714, f(x3)=0.00000
#4: x4=0.56714, f(x4)=0.00000
newton: 0.5671432904111706
#1: x1=0.60518, f(x1)=0.10845
#2: x2=0.57811, f(x2)=0.03058
#3: x3=0.57048, f(x3)=0.00924
#4: x4=0.56817, f(x4)=0.00284
#5: x5=0.56746, f(x5)=0.00088
#6: x6=0.56724, f(x6)=0.00027
#7: x7=0.56717, f(x7)=0.00008
#8: x8=0.56715, f(x8)=0.00003
#9: x9=0.56715, f(x9)=0.00001
#10: x10=0.56714, f(x10)=0.00000
#11: x11=0.56714, f(x11)=0.00000 简化牛顿法收敛更慢
simplified newton: 0.5671435739443494
#1: x1=0.61353, f(x1)=0.13316
#2: x2=0.57189, f(x2)=0.01315
#3: x3=0.56732, f(x3)=0.00049
#4: x4=0.56714, f(x4)=0.00000
#5: x5=0.56714, f(x5)=0.00000
secant: 0.5671432905092018
\qquad
4.
牛顿下山法
\textbf{4. 牛顿下山法}
4. 牛顿下山法
\qquad 牛顿法的收敛性依赖于初始值 x 0 x_0 x0 的选取,如果 x 0 x_0 x0 离方程的根 x ∗ x^{\ast} x∗ 较远,牛顿法就可能发散。
\qquad 为了防止迭代过程发散,在迭代过程中增加“单调性”的要求: ∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣ \vert f(x_{k+1})\vert<\vert f(x_{k})\vert ∣f(xk+1)∣<∣f(xk)∣,满足该要求的算法称为“下山法”。
\qquad 牛顿下山法,是将牛顿法和下山法结合起来使用——在保证函数值稳定下降的前提下,使用牛顿法加快收敛速度。
( 1 ) \qquad(1) (1) 计算牛顿法的迭代值: x ˉ k + 1 = x k − f ( x k ) f ′ ( x k ) \bar x_{k+1}=x_k-\dfrac{f(x_k)}{f^{'}(x_k)} xˉk+1=xk−f′(xk)f(xk)
( 2 ) \qquad(2) (2) 将 x ˉ k + 1 \bar x_{k+1} xˉk+1 与前一步的迭代值 x k x_{k} xk 的凸组合作为新的迭代值:
x k + 1 = λ x ˉ k + 1 + ( 1 − λ ) x k , λ ∈ ( 0 , 1 ] \qquad\qquad\qquad x_{k+1}=\lambda\bar x_{k+1}+(1-\lambda)x_{k}\ \ ,\quad\lambda\in(0,1] xk+1=λxˉk+1+(1−λ)xk ,λ∈(0,1]
\qquad
因此,牛顿下山法的迭代公式为:
x
k
+
1
=
x
k
−
λ
f
(
x
k
)
f
′
(
x
k
)
\qquad\qquad x_{k+1}=x_k-\lambda\dfrac{f(x_k)}{f^{'}(x_k)}
xk+1=xk−λf′(xk)f(xk)
\qquad 其中, λ \lambda λ 为下山因子。 λ \lambda λ 越大,表明牛顿法的迭代值 x ˉ k + 1 \bar x_{k+1} xˉk+1 越可靠; λ \lambda λ 越小,表明牛顿法的迭代值 x ˉ k + 1 \bar x_{k+1} xˉk+1 不可靠,应当尽量信任上一步的迭代值 x k x_{k} xk。
\qquad 选择下山因子 λ \lambda λ 的策略
( 1 ) \qquad(1) (1) 令 λ = 1 \lambda=1 λ=1,此时的测试点就是牛顿法的迭代值 x ˉ k + 1 \bar x_{k+1} xˉk+1
( 2 ) \qquad(2) (2) 当下山因子的值为 λ \lambda λ,测试点的值为 x ^ k + 1 = λ x ˉ k + 1 + ( 1 − λ ) x k \hat x_{k+1}=\lambda\bar x_{k+1}+(1-\lambda)x_{k} x^k+1=λxˉk+1+(1−λ)xk
( 3 ) \qquad(3) (3) 判断测试点 x ^ k + 1 \hat x_{k+1} x^k+1 是否满足“下山条件” ∣ f ( x ^ k + 1 ) ∣ < ∣ f ( x k ) ∣ \vert f(\hat x_{k+1})\vert<\vert f(x_{k})\vert ∣f(x^k+1)∣<∣f(xk)∣
\qquad 如果满足,下一步迭代点为: x k + 1 = x ^ k + 1 x_{k+1}=\hat x_{k+1} xk+1=x^k+1,开始下一次迭代过程
(
4
)
\qquad(4)
(4) 如果不满足
∣
f
(
x
^
k
+
1
)
∣
<
∣
f
(
x
k
)
∣
\vert f(\hat x_{k+1})\vert<\vert f(x_{k})\vert
∣f(x^k+1)∣<∣f(xk)∣,则将
λ
\lambda
λ 值减半,重复步骤
(
2
)
∼
(
4
)
(2)\sim(4)
(2)∼(4),直到满足“下山条件”为止。
\qquad
例
8
\textbf{例 8}
例 8 求方程
f
(
x
)
=
x
3
−
x
−
1
f(x)=x^3-x-1
f(x)=x3−x−1 在
x
0
=
0.6
x_0=0.6
x0=0.6 附近的解。
import numpy as np
def diff1_c(f,x,h):
return (f(x+h)-f(x-h))/(2*h)
def newton(f,x0,eps):
(略)
def newton_downhill(f,x0,eps):
xk = x0
lambda0 = 1
flag = 1
n = 1
print('#0: x0=%.5f, f(x0)=%.5f'%(x0,f(x0)))
while flag:
xk1 = xk - f(xk)/diff1_c(f,xk,0.001)
if np.abs(f(xk1)) < np.abs(f(xk)):
print('#%d: x%d=%.5f, f(x%d)=%.5f'%(n,n,xk1,n,f(xk1)))
else:
flag0 = 1
while flag0:
lambda0 = lambda0/2
xtest = lambda0*xk1 + (1-lambda0)*xk
if np.abs(f(xtest)) < np.abs(f(xk)):
flag0 = 0
xk1 = xtest
print('#%d: x%d=%.5f, f(x%d)=%.5f'%(n,n,xk1,n,f(xk1)))
if np.abs(xk1-xk)<eps:
val = xk1
flag = 0
xk = xk1
n += 1
return val
if __name__ == '__main__':
eps = 0.0001
f = lambda x: x**3 - x - 1
val = newton(f,0.6,eps) ## newton
print('newton:',val)
val = newton_downhill(f,0.6,eps) ## newton downhill
print('newton_downhill:',val)
计算结果:
#1: x1=17.89978, f(x1)=5716.23136 牛顿法从初值0.6直接跳到了17.9
#2: x2=11.94666, f(x2)=1692.11203
#3: x3=7.98542, f(x3)=500.22120
#4: x4=5.35685, f(x4)=147.36213
#5: x5=3.62495, f(x5)=43.00802
#6: x6=2.50556, f(x6)=12.22398
#7: x7=1.82011, f(x7)=3.20959
#8: x8=1.46104, f(x8)=0.65774
#9: x9=1.33932, f(x9)=0.06313
#10: x10=1.32491, f(x10)=0.00083
#11: x11=1.32472, f(x11)=0.00000
#12: x12=1.32472, f(x12)=0.00000
newton: 1.3247179572447556
#0: x0=0.60000, f(x0)=-1.38400
#1: x1=1.14062, f(x1)=-0.65666 下山条件会防止测试点跳到太远
#2: x2=1.36682, f(x2)=0.18666
#3: x3=1.32628, f(x3)=0.00667
#4: x4=1.32472, f(x4)=0.00001
#5: x5=1.32472, f(x5)=0.00000
newton_downhill: 1.324717957250078





















 1527
1527











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








