1、简介
1.1 什么是聚类分析
Cluster: a collection of data objects, similar to one another within the same cluster, dissimilar to the objects in other clusters. 聚类分析(Cluster analysis)就是根据数据的特征找出数据间的相似性,将相似的数据分成一个类。聚类分析是一种无监督的学习(Unsupervised learning: no predefined classes)。
1.2 Typical applications
聚类分析可以作为一个独立的工具对数据分布进行分析,也可以作为其他算法(如分类等)的预处理步骤 ,还用于Pattern Recognition、Spatial Data Analysis、Image Processing、Economic Science (especially market research)、WWW等方面。比如在Marketing方面,可以帮助市场分析人员从客户基本库中发现不同的客户群,并且用购买模式来刻画不同的客户群的特征;在Land use方面,可以在地球观测数据库中用以确定相似地区;在City-planning方面,可以根据房子的类型,价值,和地理位置对一个城市中的房屋分组。
1.3 聚类的质量
好的聚类方法能产生高质量的聚类。所谓高质量,指类中的对象高度相似、类间的对象高度不相似。聚类的质量与相似性度量及其实现方法有关。聚类方法的好坏也可以按照它是否能够发现更多的隐含模式来度量。
聚类质量的衡量关键在与相似度(或不相似程度)的计算,相似性(Dissimilarity/Similarity metric)通常用距离函数来表示,typically metric: d(i, j)。距离函数的定义对于不同的数据通常是不同的,如:interval-scaled、Boolean、Categorical、ordinal ratio、vector variables等。根据应用背景或者数据语义的不同,对不同的变量可以适当加权。其实,实际中很难定义什么是“足够相似”,答案的主观性很强。
1.4 Requirements of Clustering in Data Mining
可伸缩性、能够处理各种不同类型的属性、能够发现任意形状的聚类、在决定输入参数的时候,对领域知识的需求要小、能够处理噪声和异常点、对输入数据的顺序部敏感、可以处理高维数据、可以和用户制定的限定条件相结合、可解释性和使用性好。
2、聚类中的数据结构和相关概念
2.1 数据结构
(1) Data matrix(数据矩阵,或称为对象属性结构)
用p个变量(也称为属性)来表现n个对象,例如用年龄,身高,性别,种族等属性来表现对象“人”。这种数据结构是关系表的形式,或者看为n*p维(n个对象*p个属性)的矩阵。
图1 Data matrix(数据矩阵,或称为对象属性结构)
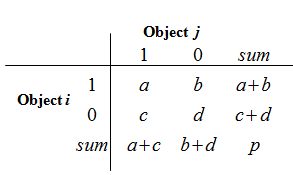
(2) Dissimilarity matrix(相异度矩阵,或称为对象-对象结构)
存储n个对象两两之间的近似性,表现形式是一个n*n维的矩阵。d(i,j)是对象i和对象j之间相异性的量化表示,通常它是一个非负的数值,当对象i 和j越相似,其值越接近0;两个对象越不同,其值越大。既然d(i,j) = d(j,i),而且d(i,i)=0,可以得到如下矩阵。
图2 Dissimilarity matrix(相异度矩阵,或称为对象-对象结构)
(3) 二模矩阵和单模矩阵
数据矩阵经常被称为二模(two-mode)矩阵,而相异度矩阵被称为单模(one-mode)矩阵。这是因为前者的行和列代表不同的实体,而后者的行和列代表相同的实体。许多聚类算法以相异度矩阵为基础。如果数据是用数据矩阵的形式表现的,在使用该类算法之前要将其转化为相异度矩阵。
2.2 数据类型
(1) Interval-scaled variables(区间标度 )
区间标度变量的典型的例子包括重量和高度,经度和纬度坐标,以及大气温度等。选用的度量单位将直接影响聚类分析的结果。例如,将高度的度量单位由“米”改为“英尺”,或者将重量的单位由“千克”改为“磅”,可能产生非常不同的聚类结构。为了避免对度量单位选择的依赖,数据应当标准化。为了实现度量值的标准化,一种方法是将原来的度量值转换为无单位的值。
1) 数据标准化
给定一个变量f的度量值,可以进行如下的变换:
2) 计算对象间的相异度
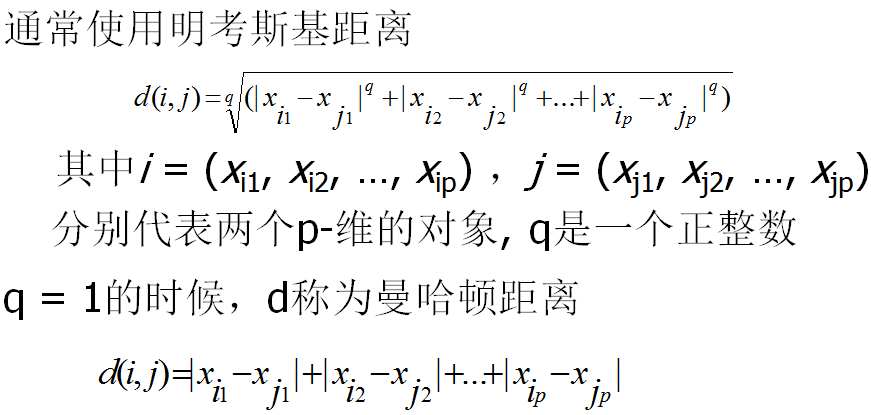


(a) 第i个对象的f值为xif,变量f有Mf个有序的状态,对应于序列1,…,Mf。用对应的rif代替xif,rif∈ {1,…,Mf}。
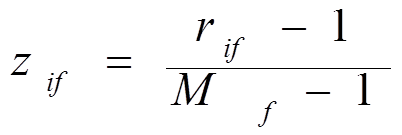
(c) 相异度的计算可以采用区间标度变量的方法,采用zif作为第i个对象的f值。
(5) Ratio-Scaled Variables(比例标度变量)
(6) Variables of Mixed (混合类变量)

给定一个n个对象或元组的数据库,划分方法构建数据的k个划分,每个划分表示一个聚类,并且k<=n。也就是说,它将数据划分为k个组,同时满足如下的要求:(1)每个组至少包含一个对象;(2)每个对象必须属于且只属于一个组。
主要思想是把数据对象排列成一个聚类树,在需要的层次上对其进行切割,相关联的部分构成一个cluster。基于层次的聚类方法有两种类型:
(1)聚合层次聚类。最初每个对象是一个cluster,然后根据它们之间的相似性,对这些原子的cluster进行合并。大多数层次方法属于这一类,它们的主要区别是cluster之间的相似性的定义不同。

绝大多数划分方法基于对象之间的距离进行聚类。这样的方法只能发现凸状的簇,而在发现任意形状的簇上遇到了困难。基于密度的聚类方法的主要思想是:只要临近区域的密度(对象或数据点的数目)超过某个阈值,就继续聚类。也就是说,对给定类中的每个数据点,在一个给定范围的区域中必须包含至少某个数目的点。这样的方法可以用来过滤“噪音”数据,发现任意形状的簇。
把多维数据空间划分成一定数目的单元,然后在这种数据结构上进行聚类操作。该类方法的特点是它的处理速度,因为其速度与数据对象的个数无关,而只依赖于数据空间中每个维上单元的个数。
3.5 基于模型的方法
(1) 神经网络方法
(2) 统计的方法

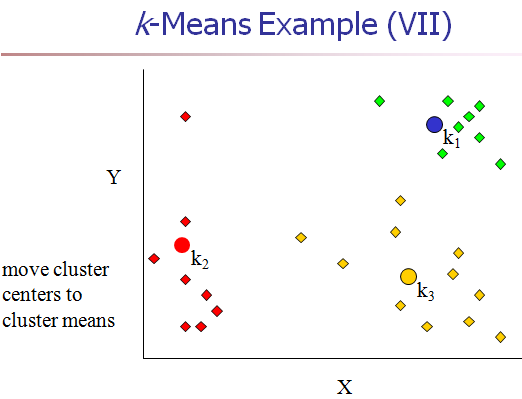
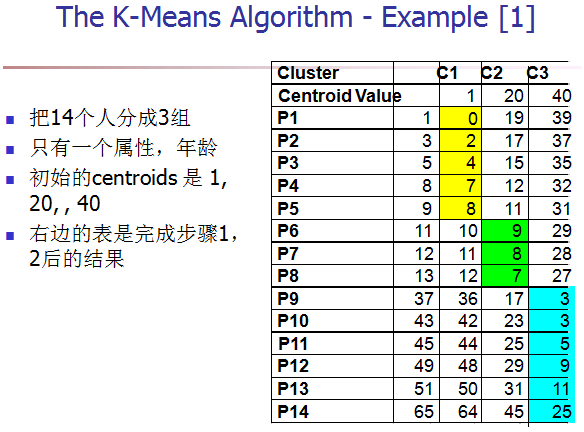
[1] 给K个cluster选择最初的中心点,称为K个Means。(这时的聚类中心依据经验或任意指定)
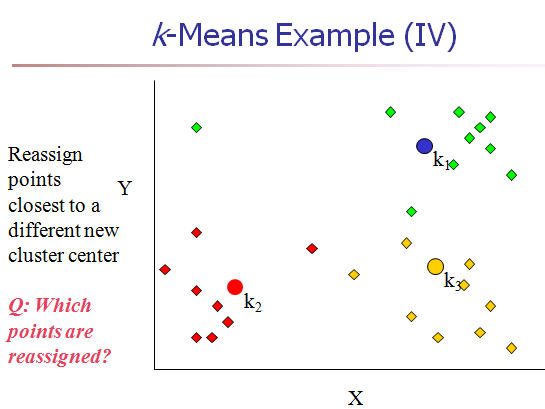
[2] 计算每个对象和每个中心点之间的距离。
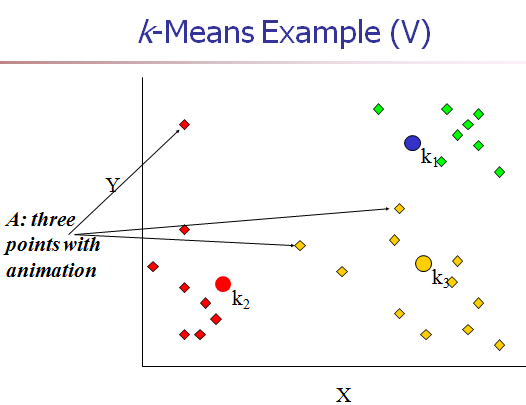
[3] 把每个对象分配给距它最近的中心点做属的cluster。
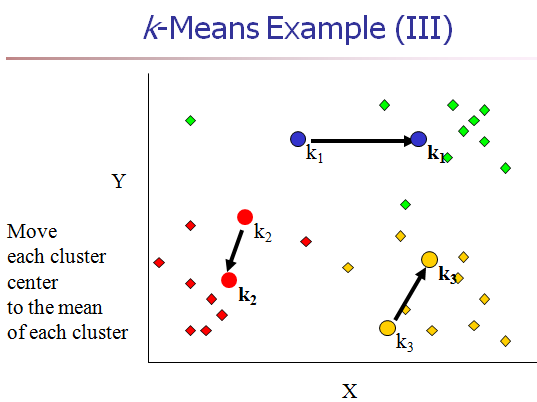
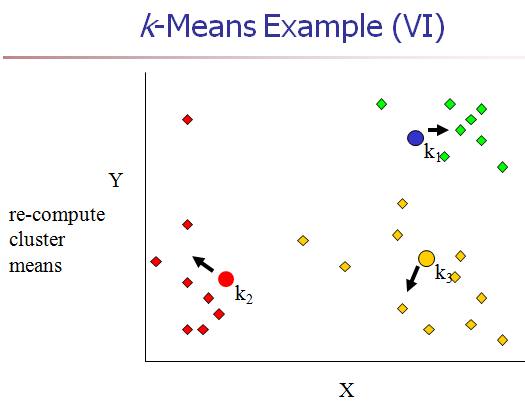
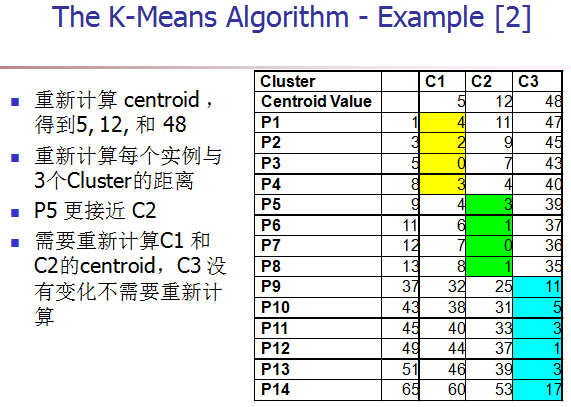
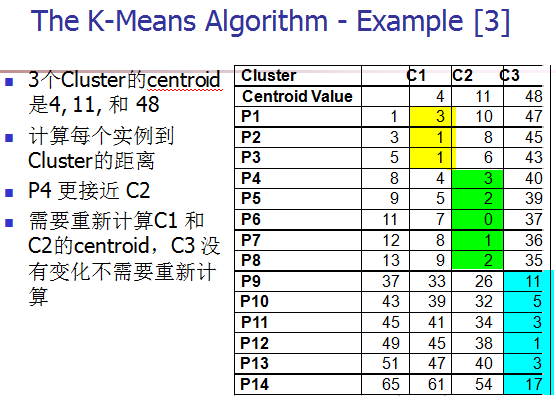
[4] 重新计算每个cluster的中心点。(K-means中新的聚类中心,由类中所有的点各维的平均值计算得来。)
[5] 重复2,3,4步,直到算法收敛。

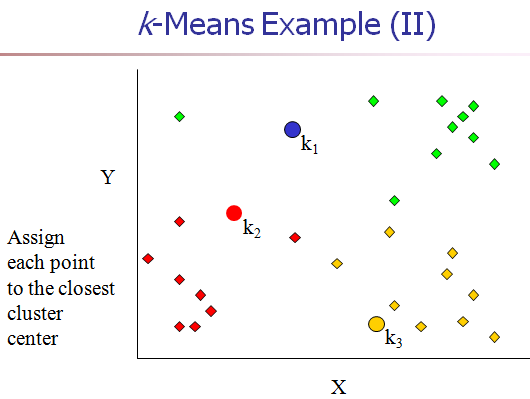
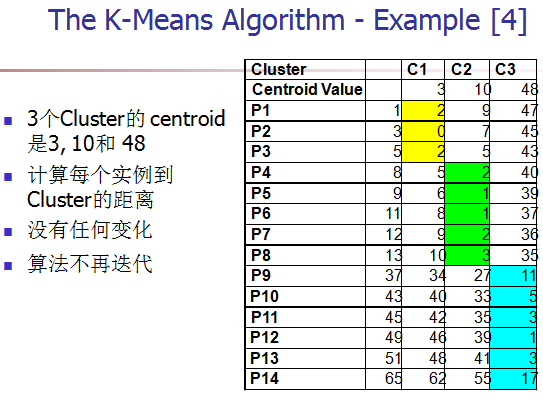
(2) 可以实现局部最优化,如果要找全局最优,可以用退火算法或者遗传算法
K-Means方法也有以下缺点:
(1) Cluster的个数必须事先确定,在有些应用中,事先并不知道cluster的个数。
(2) K个中心点必须事先预定,而对于有些字符属性,很难确定中心点。
(3) 不能处理噪音数据。
(4) 不能处理有些分布的数据(例如凹形)
(2) K-Prototypes:处理分类和数值属性
(3) K-Medoids
它们与K-Means方法的主要区别在于:
(1) 最初的K个中心点的选择不同。
(2) 距离的计算方式不同。
(3) 计算cluster的中心点的策略不同。










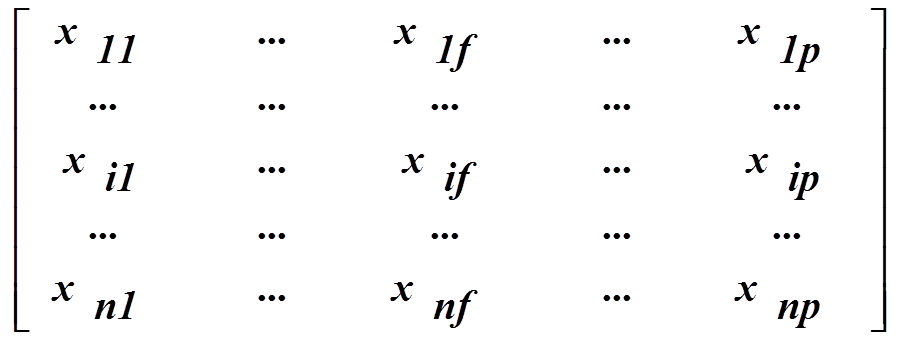
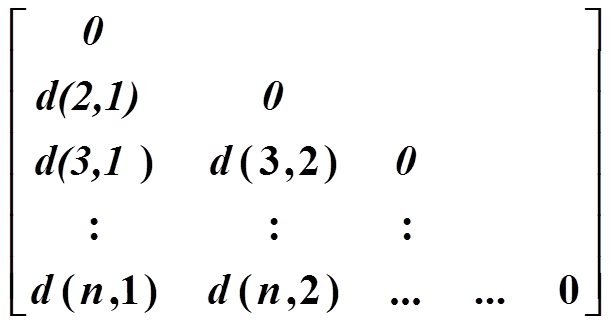















 1802
1802

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








