十大经典排序算法

最新推荐文章于 2025-07-19 12:05:38 发布

奋进学堂

最新推荐文章于 2025-07-19 12:05:38 发布

阅读量1.1k

点赞数 37

CC 4.0 BY-SA版权

文章标签：排序算法算法

本文链接：https://blog.csdn.net/xiaoaque/article/details/149412943

十大经典排序算法

本系列算法整理自：https://github.com/hustcc/JS-Sorting-Algorithm

同时也参考了维基百科做了一些补充。

排序算法是《数据结构与算法》中最基本的算法之一。

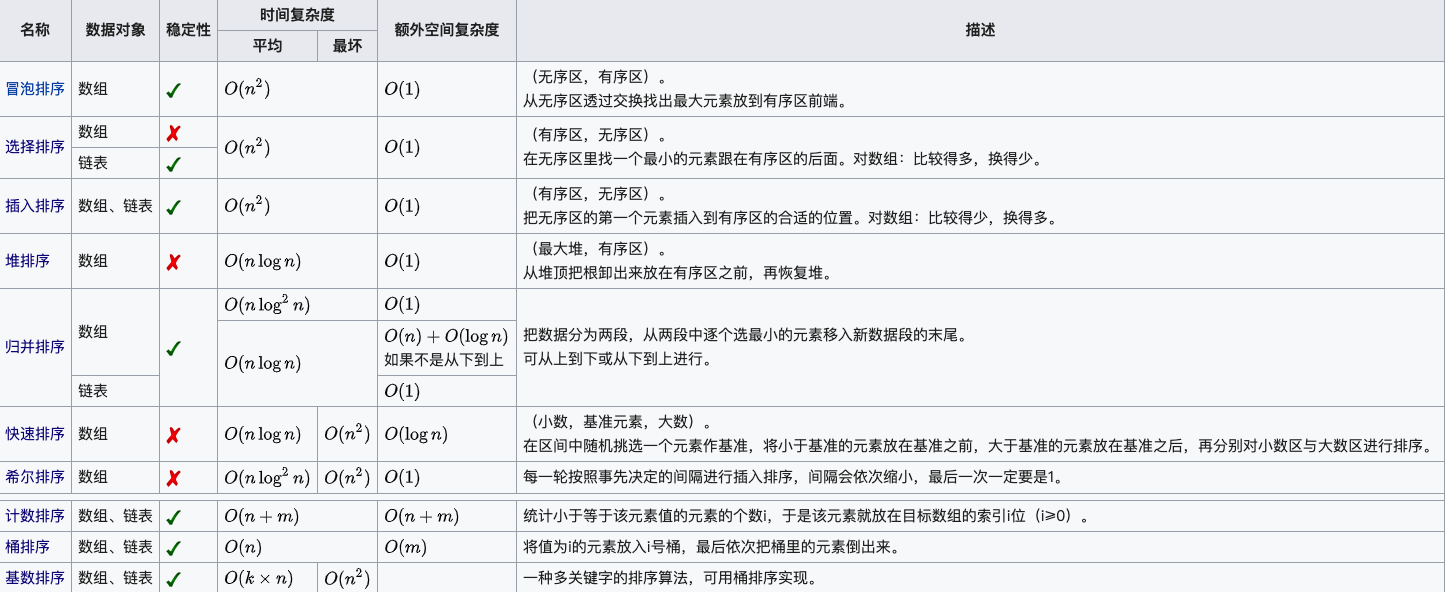
排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

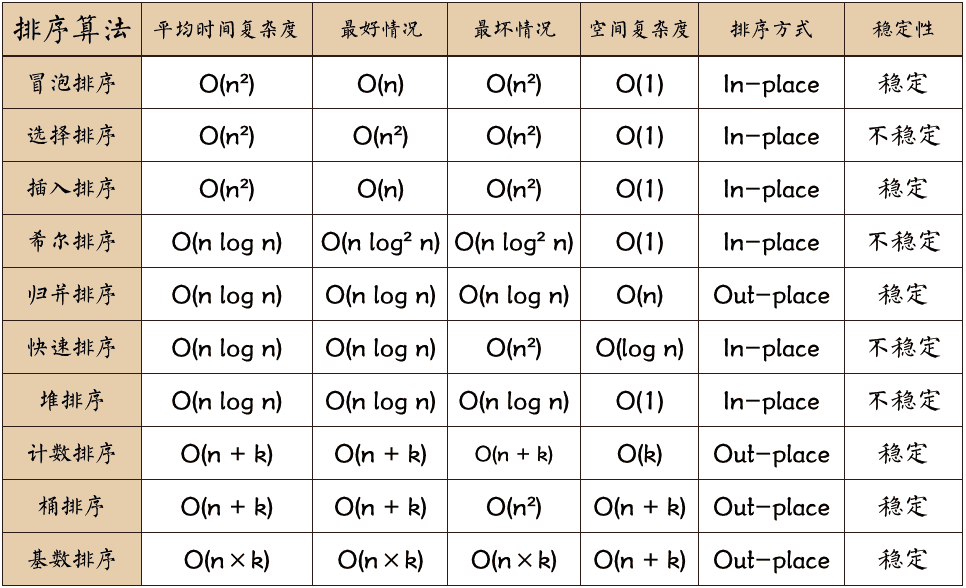
点击以下图片查看大图：

关于时间复杂度

平方阶 (O(n2)) 排序各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。希尔排序

线性阶 (O(n)) 排序基数排序，此外还有桶、箱排序。

关于稳定性

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

n：数据规模
k："桶"的个数
In-place：占用常数内存，不占用额外内存
Out-place：占用额外内存
稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同
包含以下内容：
- - 1、冒泡排序
  - 2、选择排序
  - 3、插入排序
  - 4、希尔排序
  - 5、归并排序
  - 6、快速排序
  - 7、堆排序
  - 8、计数排序
  - 9、桶排序
  - 10、基数排序
  - 1.1 冒泡排序
    
    分类算法
    
    冒泡排序（Bubble Sort）是一种简单的排序算法，它通过重复地遍历待排序的列表，比较相邻的元素并交换它们的位置来实现排序。该算法的名称来源于较小的元素会像"气泡"一样逐渐"浮"到列表的顶端。
    
    1. 算法步骤
  - 比较相邻元素：从列表的第一个元素开始，比较相邻的两个元素。
  - 交换位置：如果前一个元素比后一个元素大，则交换它们的位置。
  - 重复遍历：对列表中的每一对相邻元素重复上述步骤，直到列表的末尾。这样，最大的元素会被"冒泡"到列表的最后。
  - 缩小范围：忽略已经排序好的最后一个元素，重复上述步骤，直到整个列表排序完成。
  - 2. 动图演示
    
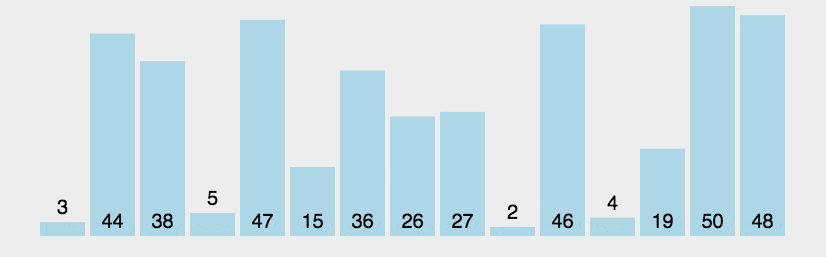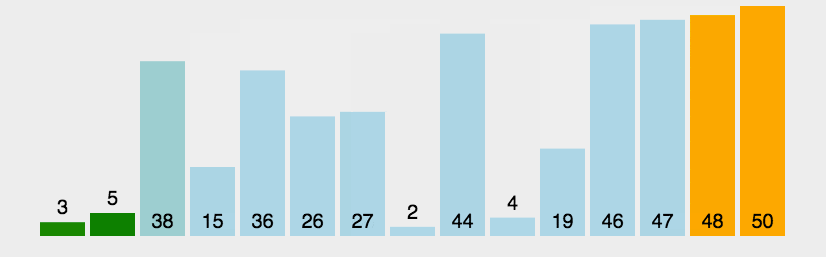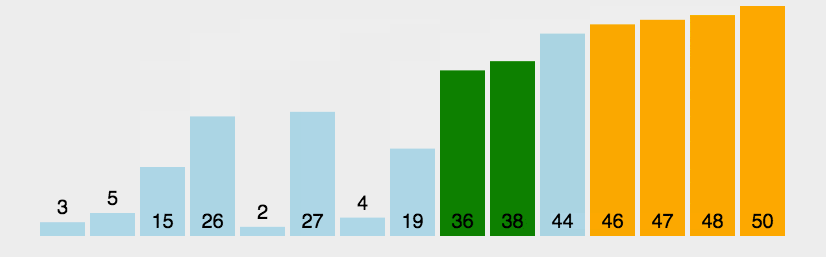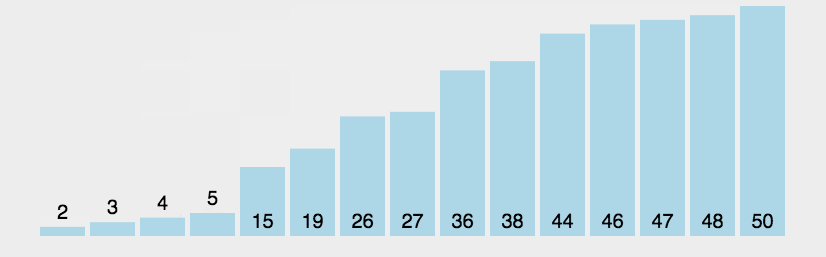
    假设有一个待排序的列表 [5, 3, 8, 4, 6]，冒泡排序的过程如下：
  - 第一轮遍历：
    - 比较 5 和 3，交换位置，列表变为 [3, 5, 8, 4, 6]。
    - 比较 5 和 8，不交换。
    - 比较 8 和 4，交换位置，列表变为 [3, 5, 4, 8, 6]。
    - 比较 8 和 6，交换位置，列表变为 [3, 5, 4, 6, 8]。
    - 第一轮结束后，最大的元素 8 已经"冒泡"到列表的最后。
  - 第二轮遍历：
    - 比较 3 和 5，不交换。
    - 比较 5 和 4，交换位置，列表变为 [3, 4, 5, 6, 8]。
    - 比较 5 和 6，不交换。
    - 第二轮结束后，第二大的元素 6 已经"冒泡"到列表的倒数第二位置。
  - 第三轮遍历：
    - 比较 3 和 4，不交换。
    - 比较 4 和 5，不交换。
    - 第三轮结束后，列表已经有序。
  - 第四轮遍历：
    - 比较 3 和 4，不交换。
    - 列表已经完全有序。
  - 实例
    
    def bubble_sort(arr):
    n = len(arr)
      for i in range(n):
      # 标记是否发生了交换
    swapped = False
      for j in range(0, n-i-1):
      if arr[j] > arr[j+1]:
      # 交换位置
    arr[j], arr[j+1] = arr[j+1], arr[j]
    swapped = True
      # 如果没有发生交换，说明列表已经有序，提前退出
      if not swapped:
      break
      return arr
    
    # 示例
    arr = [5, 3, 8, 4, 6]
    sorted_arr = bubble_sort(arr)
    print(sorted_arr)  # 输出: [3, 4, 5, 6, 8]
    
    3. 时间复杂度
  - 最坏情况：O(n²)，当列表是逆序时。
  - 最好情况：O(n)，当列表已经有序时。
  - 平均情况：O(n²)。
  - 4. 空间复杂度
  - O(1)，因为冒泡排序是原地排序算法，不需要额外的存储空间。
  - 5. 优缺点
  - 优点：
    - 实现简单，代码易于理解。
    - 原地排序，不需要额外的存储空间。
  - 缺点：
    - 效率较低，尤其是对于大规模数据集。
    - 不适合处理几乎已经有序的列表，因为仍然需要进行多次遍历。
  - 6. 什么时候最快
    
    当输入的数据已经是正序时（都已经是正序了，我还要你冒泡排序有何用啊）。
    
    7. 什么时候最慢
    
    当输入的数据是反序时（写一个 for 循环反序输出数据不就行了，干嘛要用你冒泡排序呢，我是闲的吗）。
    
    8. JavaScript 代码实现
    
    实例
    
    function bubbleSort(arr) {
      var len = arr.length;
      for (var i = 0; i < len - 1; i++) {
      for (var j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j+1]) {   // 相邻元素两两对比
      var temp = arr[j+1];   // 元素交换
    arr[j+1] = arr[j];
    arr[j] = temp;
      }
      }
      }
      return arr;
    }
    
    9. Python 代码实现
    
    实例
    
    def bubbleSort(arr):
      for i in range(1, len(arr)):
      for j in range(0, len(arr)-i):
      if arr[j] > arr[j+1]:
    arr[j], arr[j + 1] = arr[j + 1], arr[j]
      return arr
    
    10. Go 代码实现
    
    实例
    
    func bubbleSort(arr []int) []int {
    length := len(arr)
      for i := 0; i < length; i++ {
      for j := 0; j < length-1-i; j++ {
      if arr[j] > arr[j+1] {
    arr[j], arr[j+1] = arr[j+1], arr[j]
      }
      }
      }
      return arr
    }
    
    11. Java 代码实现
    
    实例
    
    public class BubbleSort implements IArraySort {
    
    @Override
      public int[] sort(int[] sourceArray) throws Exception {
      // 对 arr 进行拷贝，不改变参数内容
      int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    
      for (int i = 1; i < arr.length; i++) {
      // 设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成。
      boolean flag = true;
    
      for (int j = 0; j < arr.length - i; j++) {
      if (arr[j] > arr[j + 1]) {
      int tmp = arr[j];
    arr[j] = arr[j + 1];
    arr[j + 1] = tmp;
    
    flag = false;
      }
      }
    
      if (flag) {
      break;
      }
      }
      return arr;
      }
    }
    
    12. PHP 代码实现
    
    实例
    
    function bubbleSort($arr)
    {
      $len = count($arr);
      for ($i = 0; $i < $len - 1; $i++) {
      for ($j = 0; $j < $len - 1 - $i; $j++) {
      if ($arr[$j] > $arr[$j+1]) {
      $tmp = $arr[$j];
      $arr[$j] = $arr[$j+1];
      $arr[$j+1] = $tmp;
      }
      }
      }
      return $arr;
    }
    
    13. C 语言
    
    实例
    
    #include <stdio.h>
    void bubble_sort(int arr[], int len) {
      int i, j, temp;
      for (i = 0; i < len - 1; i++)
      for (j = 0; j < len - 1 - i; j++)
      if (arr[j] > arr[j + 1]) {
    temp = arr[j];
    arr[j] = arr[j + 1];
    arr[j + 1] = temp;
      }
    }
    int main() {
      int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
      int len = sizeof(arr) / sizeof(arr[0]);
    bubble_sort(arr, len);
      int i;
      for (i = 0; i < len; i++)
      printf("%d ", arr[i]);
      return 0;
    }
    
    14. C++ 语言
    
    实例
    
    #include <iostream>
    using namespace std;
    template<typename T> //整数或浮点数皆可使用,若要使用类(class)或结构体(struct)时必须重载大于(>)运算符
    void bubble_sort(T arr[], int len) {
      int i, j;
      for (i = 0; i < len - 1; i++)
      for (j = 0; j < len - 1 - i; j++)
      if (arr[j] > arr[j + 1])
    swap(arr[j], arr[j + 1]);
    }
    int main() {
      int arr[] = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
      int len = (int) sizeof(arr) / sizeof(*arr);
    bubble_sort(arr, len);
      for (int i = 0; i < len; i++)
      cout << arr[i] << ' ';
      cout << endl;
      float arrf[] = { 17.5, 19.1, 0.6, 1.9, 10.5, 12.4, 3.8, 19.7, 1.5, 25.4, 28.6, 4.4, 23.8, 5.4 };
    len = (float) sizeof(arrf) / sizeof(*arrf);
    bubble_sort(arrf, len);
      for (int i = 0; i < len; i++)
      cout << arrf[i] << ' '<<endl;
      return 0;
    }
    
    15. C#
    
    实例
    
    static void BubbleSort(int[] intArray) {
      int temp = 0;
      bool swapped;
      for (int i = 0; i < intArray.Length; i++)
      {
    swapped = false;
      for (int j = 0; j < intArray.Length - 1 - i; j++)
      if (intArray[j] > intArray[j + 1])
      {
    temp = intArray[j];
    intArray[j] = intArray[j + 1];
    intArray[j + 1] = temp;
      if (!swapped)
    swapped = true;
      }
      if (!swapped)
      return;
      }
    }
    
    16. Ruby
    
    实例
    
    class Array
      def bubble_sort!
      for i in 0...(size - 1)
      for j in 0...(size - i - 1)
      self[j], self[j + 1] = self[j + 1], self[j] if self[j] > self[j + 1]
      end
      end
      self
      end
    end
    
    puts [22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70].bubble_sort!
    
    17. Swift
    
    实例
    
    import Foundation
    
    func bubbleSort (arr: inout [Int]) {
      for i in 0..<arr.count - 1 {
      for j in 0..<arr.count - 1 - i {
      if arr[j] > arr[j+1] {
    arr.swapAt(j, j+1)
      }
      }
      }
    }
    
    // 测试调用
    
    func testSort () {
      // 生成随机数数组进行排序操作
    var list:[Int] = []
      for _ in 0...99 {
    list.append(Int(arc4random_uniform(100)))
      }
    print("\(list)")
    bubbleSort(arr:&list)
    print("\(list)")
    }
  - 1.2 选择排序
    
    分类算法
    
    选择排序（Selection Sort）是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
    
    选择排序基本思想是每次从待排序的数据中选择最小（或最大）的元素，放到已排序序列的末尾，直到全部数据排序完成。
    
    1. 算法步骤
  - 初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分为空，未排序部分为整个列表。
  - 查找最小值：在未排序部分中查找最小的元素。
  - 交换位置：将找到的最小元素与未排序部分的第一个元素交换位置。
  - 更新范围：将未排序部分的起始位置向后移动一位，扩大已排序部分的范围。
  - 重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。
  - 2. 动图演示
    
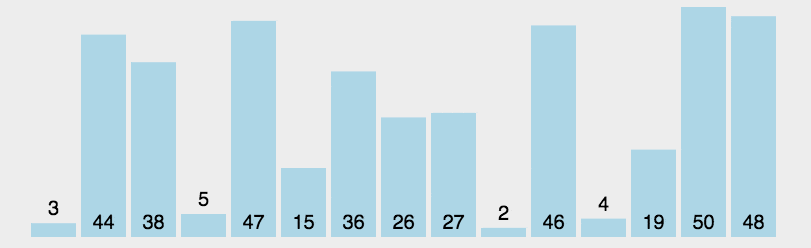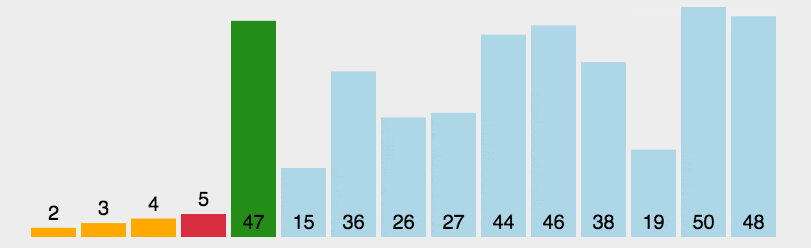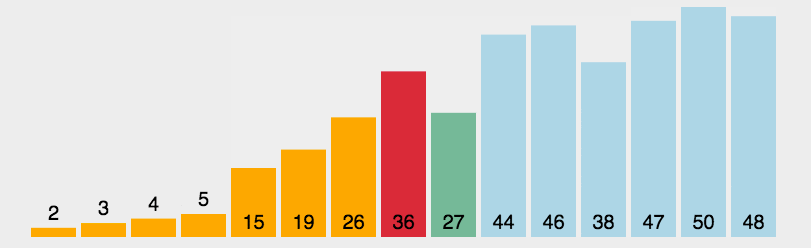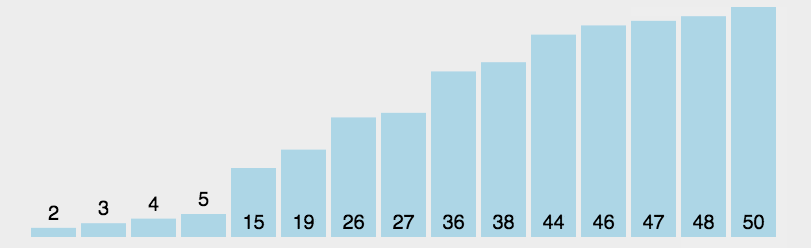
    假设有一个待排序的列表 [64, 25, 12, 22, 11]，选择排序的过程如下：
  - 第一轮：
    - 未排序部分：[64, 25, 12, 22, 11]。
    - 找到最小值 11，将其与第一个元素 64 交换。
    - 列表变为 [11, 25, 12, 22, 64]。
    - 已排序部分：[11]，未排序部分：[25, 12, 22, 64]。
  - 第二轮：
    - 未排序部分：[25, 12, 22, 64]。
    - 找到最小值 12，将其与第一个元素 25 交换。
    - 列表变为 [11, 12, 25, 22, 64]。
    - 已排序部分：[11, 12]，未排序部分：[25, 22, 64]。
  - 第三轮：
    - 未排序部分：[25, 22, 64]。
    - 找到最小值 22，将其与第一个元素 25 交换。
    - 列表变为 [11, 12, 22, 25, 64]。
    - 已排序部分：[11, 12, 22]，未排序部分：[25, 64]。
  - 第四轮：
    - 未排序部分：[25, 64]。
    - 找到最小值 25，它已经在正确的位置，无需交换。
    - 列表保持不变：[11, 12, 22, 25, 64]。
    - 已排序部分：[11, 12, 22, 25]，未排序部分：[64]。
  - 第五轮：
    - 未排序部分：[64]。
    - 只有一个元素，无需操作。
    - 列表完全有序：[11, 12, 22, 25, 64]。
  - 实例
    
    def selection_sort(arr):
    n = len(arr)
      for i in range(n):
      # 假设当前未排序部分的第一个元素是最小值
    min_idx = i
      # 在未排序部分中查找最小值的索引
      for j in range(i+1, n):
      if arr[j] < arr[min_idx]:
    min_idx = j
      # 将最小值与未排序部分的第一个元素交换
    arr[i], arr[min_idx] = arr[min_idx], arr[i]
      return arr
    
    # 示例
    arr = [64, 25, 12, 22, 11]
    sorted_arr = selection_sort(arr)
    print(sorted_arr)  # 输出: [11, 12, 22, 25, 64]
    
    时间复杂度
  - 最坏情况：O(n²)，无论输入数据是否有序，都需要进行 n(n-1)/2 次比较。
  - 最好情况：O(n²)，即使列表已经有序，仍需进行相同数量的比较。
  - 平均情况：O(n²)。
  - 空间复杂度
  - O(1)，选择排序是原地排序算法，不需要额外的存储空间。
  - 优缺点
  - 优点：
    - 实现简单，代码易于理解。
    - 原地排序，不需要额外的存储空间。
    - 对于小规模数据集，性能尚可接受。
  - 缺点：
    - 时间复杂度较高，不适合大规模数据集。
    - 不稳定排序算法（如果存在相同元素，可能会改变它们的相对顺序）。
  - 适用场景
  - 数据量较小且对性能要求不高的场景。
  - 需要简单实现的场景。
  - C 语言
    
    实例
    
    void swap(int *a,int *b) //交換兩個變數
    {
      int temp = *a;
      *a = *b;
      *b = temp;
    }
    void selection_sort(int arr[], int len)
    {
      int i,j;
    
      for (i = 0 ; i < len - 1 ; i++)
      {
      int min = i;
      for (j = i + 1; j < len; j++)     //走訪未排序的元素
      if (arr[j] < arr[min])   //找到目前最小值
    min = j;   //紀錄最小值
    swap(&arr[min], &arr[i]);   //做交換
      }
    }
    
    C++
    
    实例
    
    template<typename T> //整數或浮點數皆可使用，若要使用物件（class）時必須設定大於（>）的運算子功能
    void selection_sort(std::vector<T>& arr) {
      for (int i = 0; i < arr.size() - 1; i++) {
      int min = i;
      for (int j = i + 1; j < arr.size(); j++)
      if (arr[j] < arr[min])
    min = j;
    std::swap(arr[i], arr[min]);
      }
    }
    
    C#
    
    实例
    
    static void selection_sort<T>(T[] arr) where T : System.IComparable<T>{//整數或浮點數皆可使用
      int i, j, min, len = arr.Length;
    T temp;
      for (i = 0; i < len - 1; i++) {
    min = i;
      for (j = i + 1; j < len; j++)
      if (arr[min].CompareTo(arr[j]) > 0)
    min = j;
    temp = arr[min];
    arr[min] = arr[i];
    arr[i] = temp;
      }
    }
    
    Swift
    
    实例
    
    import Foundation
    /// 选择排序
    ///
    /// - Parameter list: 需要排序的数组
    func selectionSort(_ list: inout [Int]) -> Void {
      for j in 0..<list.count - 1 {
    var minIndex = j
      for i in j..<list.count {
      if list[minIndex] > list[i] {
    minIndex = i
      }
      }
    list.swapAt(j, minIndex)
      }
    
    代码实现
    
    JavaScript 代码实现
    
    实例
    
    function selectionSort(arr) {
      var len = arr.length;
      var minIndex, temp;
      for (var i = 0; i < len - 1; i++) {
    minIndex = i;
      for (var j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {     // 寻找最小的数
    minIndex = j;     // 将最小数的索引保存
      }
      }
    temp = arr[i];
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
      }
      return arr;
    }
    
    Python 代码实现
    
    实例
    
    def selectionSort(arr):
      for i in range(len(arr) - 1):
      # 记录最小数的索引
    minIndex = i
      for j in range(i + 1, len(arr)):
      if arr[j] < arr[minIndex]:
    minIndex = j
      # i 不是最小数时，将 i 和最小数进行交换
      if i != minIndex:
    arr[i], arr[minIndex] = arr[minIndex], arr[i]
      return arr
    
    Go 代码实现
    
    实例
    
    func selectionSort(arr []int) []int {
    length := len(arr)
      for i := 0; i < length-1; i++ {
    min := i
      for j := i + 1; j < length; j++ {
      if arr[min] > arr[j] {
    min = j
      }
      }
    arr[i], arr[min] = arr[min], arr[i]
      }
      return arr
    }
    
    Java 代码实现
    
    实例
    
    public class SelectionSort implements IArraySort {
    
    @Override
      public int[] sort(int[] sourceArray) throws Exception {
      int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
    
      // 总共要经过 N-1 轮比较
      for (int i = 0; i < arr.length - 1; i++) {
      int min = i;
    
      // 每轮需要比较的次数 N-i
      for (int j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[min]) {
      // 记录目前能找到的最小值元素的下标
    min = j;
      }
      }
    
      // 将找到的最小值和i位置所在的值进行交换
      if (i != min) {
      int tmp = arr[i];
    arr[i] = arr[min];
    arr[min] = tmp;
      }
    
      }
      return arr;
      }
    }
    
    PHP 代码实现
    
    实例
    
    function selectionSort($arr)
    {
      $len = count($arr);
      for ($i = 0; $i < $len - 1; $i++) {
      $minIndex = $i;
      for ($j = $i + 1; $j < $len; $j++) {
      if ($arr[$j] < $arr[$minIndex]) {
      $minIndex = $j;
      }
      }
      $temp = $arr[$i];
      $arr[$i] = $arr[$minIndex];
      $arr[$minIndex] = $temp;
      }
      return $arr;
    }

1.3 插入排序

分类算法

插入排序（Insertion Sort）是一种简单直观的排序算法，它的工作原理类似于整理扑克牌。

插入排序通过构建有序序列，对于未排序的数据，在已排序序列中从后向前扫描，找到相应位置并插入。

插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。

插入排序和冒泡排序一样，也有一种优化算法，叫做拆半插入。

1. 算法步骤

初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分只包含第一个元素，未排序部分包含剩余元素。
选择元素：从未排序部分中取出第一个元素。
插入到已排序部分：将该元素与已排序部分的元素从后向前依次比较，找到合适的位置插入。
重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

2. 动图演示

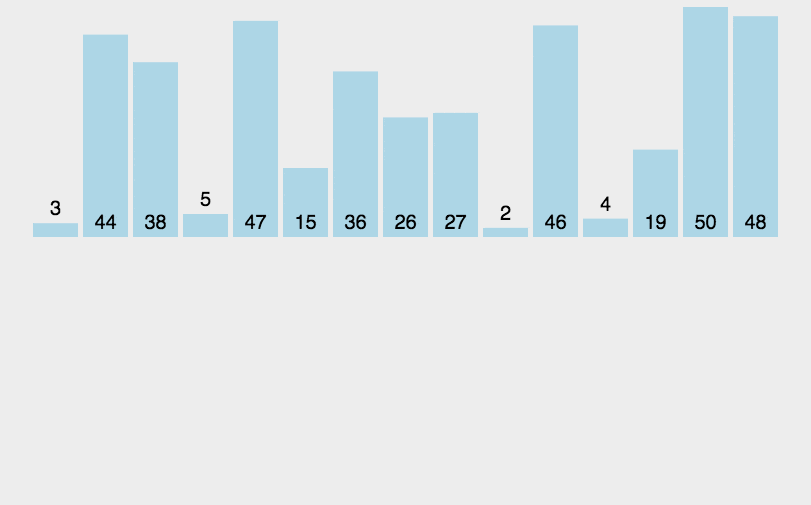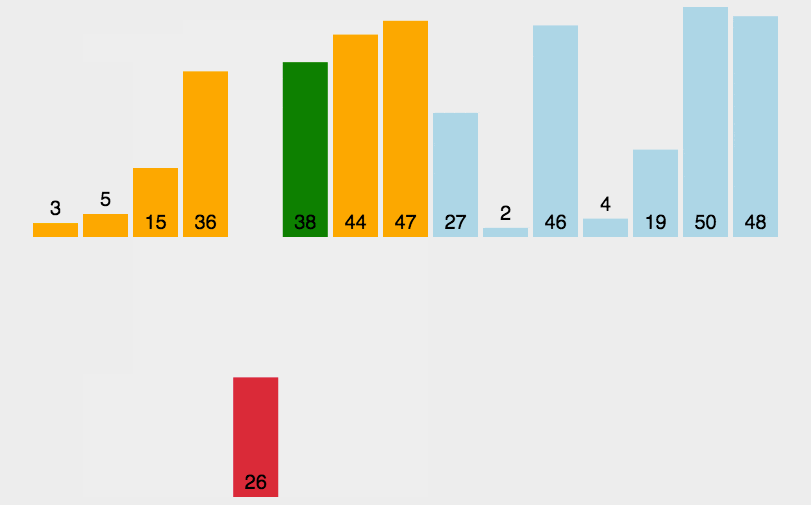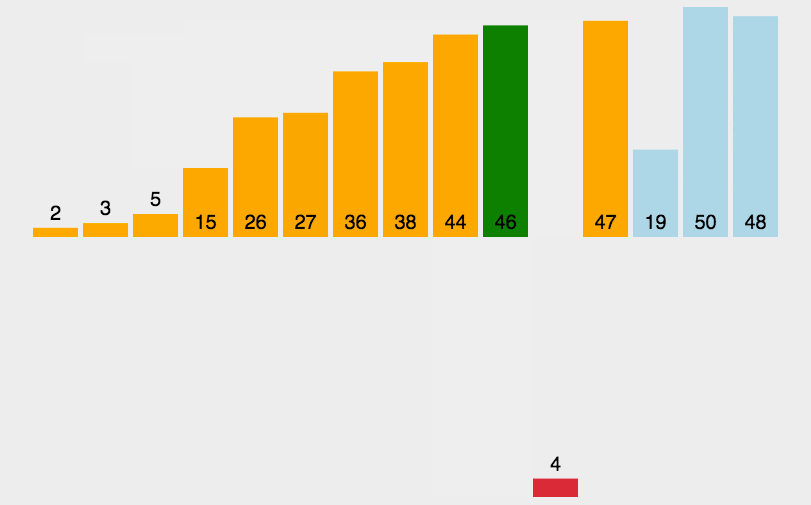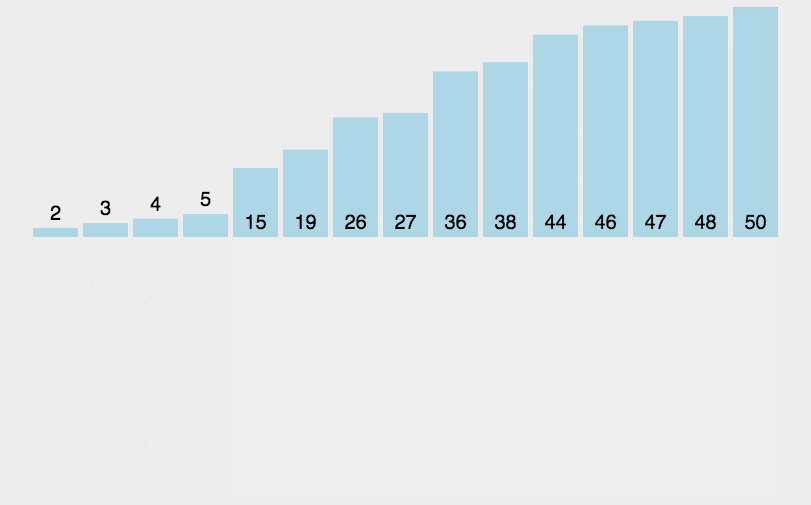
假设有一个待排序的列表 [5, 2, 4, 6, 1, 3]，插入排序的过程如下：

初始状态：
- 已排序部分：[5]。
- 未排序部分：[2, 4, 6, 1, 3]。
第一轮：
- 取出未排序部分的第一个元素 2。
- 将 2 与已排序部分的 5 比较，2 < 5，插入到 5 前面。
- 列表变为 [2, 5, 4, 6, 1, 3]。
- 已排序部分：[2, 5]，未排序部分：[4, 6, 1, 3]。
第二轮：
- 取出未排序部分的第一个元素 4。
- 将 4 与已排序部分的 5 比较，4 < 5，继续与 2 比较，4 > 2，插入到 2 和 5 之间。
- 列表变为 [2, 4, 5, 6, 1, 3]。
- 已排序部分：[2, 4, 5]，未排序部分：[6, 1, 3]。
第三轮：
- 取出未排序部分的第一个元素 6。
- 将 6 与已排序部分的 5 比较，6 > 5，直接插入到末尾。
- 列表变为 [2, 4, 5, 6, 1, 3]。
- 已排序部分：[2, 4, 5, 6]，未排序部分：[1, 3]。
第四轮：
- 取出未排序部分的第一个元素 1。
- 将 1 与已排序部分的 6 比较，1 < 6，继续与 5、4、2 比较，1 是最小的，插入到最前面。
- 列表变为 [1, 2, 4, 5, 6, 3]。
- 已排序部分：[1, 2, 4, 5, 6]，未排序部分：[3]。
第五轮：
- 取出未排序部分的第一个元素 3。
- 将 3 与已排序部分的 6 比较，3 < 6，继续与 5、4、2 比较，3 > 2，插入到 2 和 4 之间。
- 列表变为 [1, 2, 3, 4, 5, 6]。
- 已排序部分：[1, 2, 3, 4, 5, 6]，未排序部分为空。

实例

def insertion_sort(arr):
n = len(arr)
  for i in range(1, n):
key = arr[i]  # 取出未排序部分的第一个元素
j = i - 1
  # 将 key 插入到已排序部分的正确位置
  while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]  # 向后移动元素
j -= 1
arr[j + 1] = key # 插入 key
  return arr

# 示例
arr = [5, 2, 4, 6, 1, 3]
sorted_arr = insertion_sort(arr)
print(sorted_arr)  # 输出: [1, 2, 3, 4, 5, 6]