散列表概述
散列表就是一种以 键-值(key-indexed) 存储数据的结构,我们只要输入待查找的值即key,即可查找到其对应的值。
散列表的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
散列的查找算法有两个步骤:
1.使用散列函数将被查找的键转换为数组的索引。在理想的情况下,不同的键会被转换为不同的索引值,但是在有些情况下我们需要处理多个键被哈希到同一个索引值的情况。所以散列查找的第二个步骤就是处理碰撞冲突。
2.处理碰撞冲突。有很多处理散列碰撞冲突的方法,主要分为拉链法和线性探测法。
散列表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制,那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1);如果没有时间限制,那么我们可以使用无序数组并进行顺序查找,这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
散列函数和键的类型有关。对于每种类型的键我们都需要一个与之对应的散列函数。
散列函数
1. 正整数
获取正整数散列值最常用的方法是使用除留余数法。即对于大小为素数M的数组,对于任意正整数k,计算k除以M的余数。M一般取素数。
2. 字符串
将字符串作为键的时候,我们也可以将他作为一个大的整数,采用保留除余法。我们可以将组成字符串的每一个字符取值然后进行散列
char[] s = str.ToCharArray();
int hash = 0;
for (int i = 0; i < s.Length; i++)
{
hash = s[i] + (31 * hash);
}
return hash;
上面的散列值是Horner计算字符串散列值的方法,公式为:
h = s[0] · 31L–1 + … + s[L – 3] · 312 + s[L – 2] · 311 + s[L – 1] · 310
举个例子,比如要获取”call”的哈希值,字符串c对应的unicode为99,a对应的unicode为97,L对应的unicode为108,所以字符串”call”的散列值为 3045982 = 99·313 + 97·312 + 108·311 + 108·310 = 108 + 31· (108 + 31 · (97 + 31 · (99)))
如果对每个字符去散列值可能会比较耗时,所以可以通过间隔取N个字符来获取散列值来节省时间,比如,可以 获取每8-9个字符来获取散列值:
char[] s = str.ToCharArray();
int hash = 0;
int skip = Math.Max(1, s.Length / 8);
for (int i = 0; i < s.Length; i+=skip)
{
hash = s[i] + (31 * hash);
}
return hash;
3.Double类型
@Override
public int hashCode() {
return Double.hashCode(value);
}
public static int hashCode(double value) {
long bits = doubleToLongBits(value);
return (int)(bits ^ (bits >>> 32));
}
Double类的hashCode方法首先会将它的值转为long类型,然后返回低32位和高32位的异或的结果作为hashCode。
4.非数值类型对象
前面我们介绍的数据类型都可以看做一种数值型(String可以看做一个整型数组),那么对于非数值类型对象的hashCode要怎么计算呢,这里我们以Date类为例简单的介绍一下。Date类的hashCode方法如下:
public int hashCode() {
long ht = this.getTime();
return (int) ht ^ (int) (ht >> 32);
}
它的hashCode方法的实现非常简单,只是返回了Date对象所封装的时间的低32位和高32位的异或结果。从Date类的hashCode的实现我们可以了解到,对于非数值类型的hashCode的计算,我们需要选取一些能区分各个类实例的实例域来作为计算的因子。比如对于Date类来说,通常具有相同的时间的Date对象我们认为它们相等,因此也就具有相同的hashCode。这里我们需要说明一下,对于等价的两个对象(也就是调用equals方法返回true),它们的hashCode必须相同,而反之则不然。
使用拉链法处理碰撞
散列算法的第二步就是碰撞处理,也就是处理两个或多个键的散列值相同的情况。
通过散列函数,我们可以将键转换为数组的索引(0-M-1),但是对于两个或者多个键具有相同索引值的情况,我们需要有一种方法来处理这种冲突。
一种比较直接的办法就是,将大小为M 的数组的每一个元素指向一个条链表,链表中的每一个节点都存储散列值为该索引的键值对,这就是拉链法。
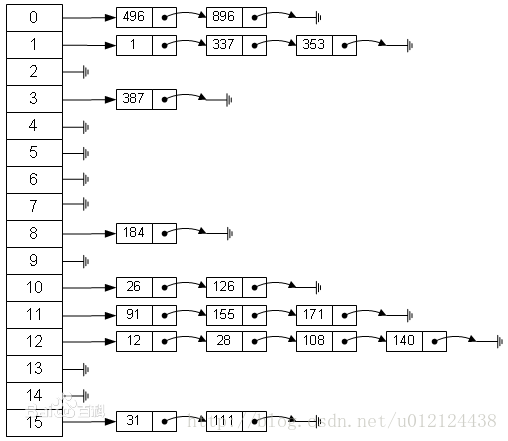
该方法的基本思想就是选择足够大的M,使得所有的链表都尽可能的短小,以保证查找的效率。对采用拉链法的哈希实现的查找分为两步,首先是根据散列值找到等一应的链表,然后沿着链表顺序找到相应的键。
拉链法的实现
public class SeperateChainingHashSet<K, V> {
private int num;
private int capacity;
private SeqSearchST<K, V>[] st;
public SeperateChainingHashSet(int initialCapacity) {
capacity = initialCapacity;
st = (SeqSearchST<K, V>[]) new Object[capacity];
for (int i = 0; i < capacity; i++) {
st[i] = new SeqSearchST<>();
}
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % capacity;
}
public V get(K key) {
return st[hash(key)].get(key);
}
public void put(K key, V value) {
st[hash(key)].put(key, value);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
在上面的实现中,我们固定了散列表的容量,当我们明确知道我们要插入的键值对数目最多只能到达桶数的常数倍时,固定容量是完全可行的。但是若键值对数目会增长到远远大于桶数,我们就需要动态调整容量的能力。实际上,散列表中的键值对数与容量的比值叫做负载因子(load factor)。通常负载因子越小,我们进行查找所需时间就越短,而空间的使用就越大;若负载因子较大,则查找时间会变长,但是空间使用会减小。比如,Java标准库中的HashMap就是基于拉链法实现的散列表,它的默认负载因子为0.75。HashMap实现动态调整容量的方式是基于公式loadFactor = maxSize / capacity,其中maxSize为支持存储的最大键值对数,而loadFactor和capacity(容量)都会在初始化时由用户指定或是由系统赋予默认值。当HashMap中的键值对的数目达到了maxSize时,就会增大散列表中的容量。
以上代码中还用到了SeqSearchST,实际上这就是一个基于链表的符号表实现
public class SeqSearchST<K, V> {
private Node first;
private class Node {
K key;
V val;
Node next;
public Node(K key, V val, Node next) {
this.key = key;
this.val = val;
this.next = next;
}
}
public V get(K key) {
for (Node node = first; node != null; node = node.next) {
if (key.equals(node.key)) {
return node.val;
}
}
return null;
}
public void put(K key, V val) {
Node node;
for (node = first; node != null; node = node.next) {
if (key.equals(node.key)) {
node.val = val;
return;
}
}
first = new Node(key, val, first);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
使用线性探测法处理碰撞
基本原理
线性探测法是另一种散列表的实现策略的具体方法,这种策略叫做开放定址法。开放定址法的主要思想是:用大小为M的数组保存N个键值对,其中M > N,数组中的空位用于解决碰撞问题。
线性探测法的主要思想是:当发生碰撞时(一个键被散列到一个已经有键值对的数组位置),我们会检查数组的下一个位置,这个过程被称作线性探测。线性探测可能会产生三种结果:
1.命中:该位置的键与要查找的键相同;
2.未命中:该位置为空;
3.该位置的键和被查找的键不同。
当我们查找某个键时,首先通过散列函数得到一个数组索引后,之后我们就开始检查相应位置的键是否与给定键相同,若不同则继续查找(若到数组末尾也没找到就折回数组开头),直到找到该键或遇到一个空位置。由线性探测的过程我们可以知道,若数组已满的时候我们再向其中插入新键,会陷入无限循环之中。
代码实现
我们使用数组keys保存散列表中的键,数组values保存散列表中的值,两个数组同一位置上的元素共同确定一个散列表中的键值对。
public class LinearProbingHashMap<K, V> {
private int num;
private int capacity;
private K[] keys;
private V[] values;
public LinearProbingHashMap(int capacity) {
keys = (K[]) new Object[capacity];
values = (V[]) new Object[capacity];
this.capacity = capacity;
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % capacity;
}
public V get(K key) {
int index = hash(key);
while (keys[index] != null && !key.equals(keys[index])) {
index = (index + 1) % capacity;
}
return values[index];
}
public void put(K key, V value) {
if (num >= capacity / 2) {
resize(2 * capacity);
}
int index = hash(key);
while (keys[index] != null && !key.equals(keys[index])) {
index = (index + 1) % capacity;
}
if (keys[index] == null) {
keys[index] = key;
values[index] = value;
return;
}
values[index] = value;
num++;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
删除操作
public void delete(K key) {
if (!contains(key)) {
return;
}
int index = hash(key);
while (!key.equals(keys[index])) {
index = (index + 1) % capacity;
}
keys[index] = null;
values[index] = null;
index = (index + 1) % capacity;
while (keys[index] != null) {
K keyToRedo = keys[index];
V valueToRedo = values[index];
keys[index] = null;
values[index] = null;
num--;
put(keyToRedo, valueToRedo);
index = (index + 1) % capacity;
}
num--;
if (num > 0 && num == capacity / 8) {
resize(capacity / 8);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
和拉链法一样,开放地址类的散列表的性能也依赖于α=num/capacity的比值 ,我们将α成为散列表的使用率。α是表中已被占用的空间的比例,它是不可能大于1的。LinearProbingHashMap中我们不允许α达到1(散列表被占满),因此未命中的查找会导致无限循环。为了保证性能,我们会动态调整数组的大小来保证使用率在1/8到1/2之间。
动态调整数组大小
在实际应用中,当负载因子(键值对数与数组大小的比值)接近1时,查找操作的时间复杂度会接近O(n),当负载因子(键值对数与数组大小的比值)接近1时,而数组的容量又是固定的时候,while循环会变为一个无限循环。所以有必要实现动态增长数组来保持查找操作的常数时间复杂度。当键值对总数很小时,若空间比较紧张,可以动态缩小数组,这取决于实际情况。
也就是put方法中的这段代码
if (num >= capacity / 2) {
resize(2 * capacity);
}
resize方法:
private void resize(int i) {
LinearProbingHashMap<K, V> hashmap = new LinearProbingHashMap<>(newCapacity);
for (int i = 0; i < capacity; i++) {
if (keys[i] != null) {
hashmap.put(keys[i], values[i]);
}
}
keys = hashmap.keys;
values = hashmap.values;
capacity = hashmap.capacity;
}
关于负载因子与查找操作的性能的关系,《算法》(Sedgewick等)中是这么说明的:
在一张大小为M并含有N = a*M(a为负载因子)个键的基于线性探测的散列表中,若散列函数满足均匀散列假设,命中和未命中的查找所需的探测次数分别为:~ 1/2 * (1 + 1/(1-a))和~1/2*(1 + 1/(1-a)^2)
关于以上结论,我们只需要知道当a约为1/2时,查找命中和未命中所需的探测次数分别为1.5次和2.5次。还有一点就是当a趋近于1时,以上结论中的估计值的精度会下降,不过我们在实际应用中不会让负载因子接近1,为了保持良好的性能,在上面的实现中我们应保持a不超过1/2。
完美散列
当关键字的集合是一个不变的静态集合(Static)时,散列技术还可以用来获取出色的最坏情况性能。如果某一种散列技术在进行查找时,其最坏情况的内存访问次数为 O(1) 时,则称其为完美散列
设计完美散列的基本思想是利用两级的散列策略,而每一级上都使用全域散列(Univeral Hashing)。
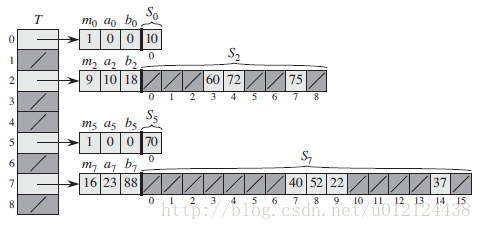
第一级与使用拉链法(chaining)的散列表基本上是一样的,利用从某一全域散列函数族中随机选择的一个函数 h ,将 n 个关键字哈希到 m 个槽中。
而此时,不像链接技术中对槽使用链表结构,而是采用一个较小的二次散列表 Sj ,与其相关的哈希函数为 hj 。通过随机的选取散列函数 hj ,可以确保在第二级上不出现散列冲突。
如果利用从一个全域散列函数族中随机选择的散列函数 h,将 n 个关键字存储在一个大小为 m = n2 的散列表中,那么出现碰撞的概率小于 1/2 。
为了确保第二级上不出现散列冲突,需要让散列表 Sj 的大小 mj 为散列到槽 j 中的关键字数 nj 的平方。mj 对 nj 的这种二次依赖关系看上去可能使得总体存储需求很大,但通过适当地选择第一次散列函数,预期使用的的总存储空间仍为 O(n)。
如果关键字的数量 n 等于槽的数量 m ,则该散列函数称为最小完美散列函数(Minimal Perfect Hash Function)。
布谷鸟散列
布谷鸟散列概述
定义:
CuckooHash(布谷鸟散列)是为了解决哈希冲突问题而提出,利用较少的计算换取较大的空间。
特点:
占用空间少,查询速度快。
算法描述:
使用hashA、hashB计算对应的key位置:
1、两个位置均为空,则任选一个插入;
2、两个位置中一个为空,则插入到空的那个位置
3、两个位置均不为空,则踢出一个位置后插入,被踢出的对调用该算法,再执行该算法找其另一个位置,循环直到插入成功。
4、如果被踢出的次数达到一定的阈值,则认为hash表已满,并进行重新哈希rehash
cuckoo hashing的哈希函数是成对的(具体的实现可以根据需求设计),每一个元素都是两个,分别映射到两个位置,一个是记录的位置,另一个是备用位置。这个备用位置是处理碰撞时用的,cuckoo hashing处理碰撞的方法,就是把原来占用位置的这个元素踢走,不过被踢出去的元素还有一个备用位置可以安置,如果备用位置上还有人,再把它踢走,如此往复。直到被踢的次数达到一个上限,才确认哈希表已满,并执行rehash操作。
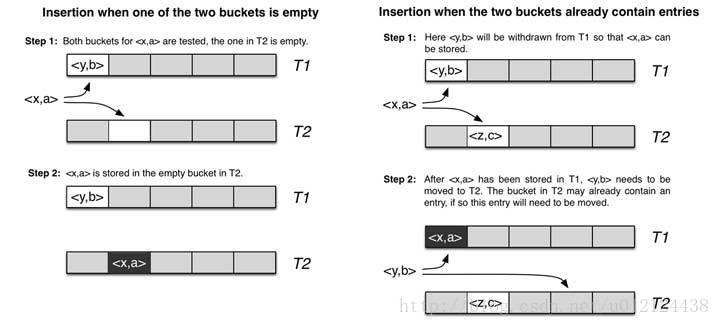
一维数组的哈希表上跟其它哈希函数没什么区别,也就50%
一个改进的哈希表如下图所示,每个桶(bucket)有4路槽位(slot)。当哈希函数映射到同一个bucket中,在其它三路slot未被填满之前,是不会有元素被踢的,这大大缓冲了碰撞的几率。笔者自己的简单实现上测过,采用二维哈希表(4路slot)大约80%的占用率(CMU论文数据据说达到90%以上,应该是扩大了slot关联数目所致)。
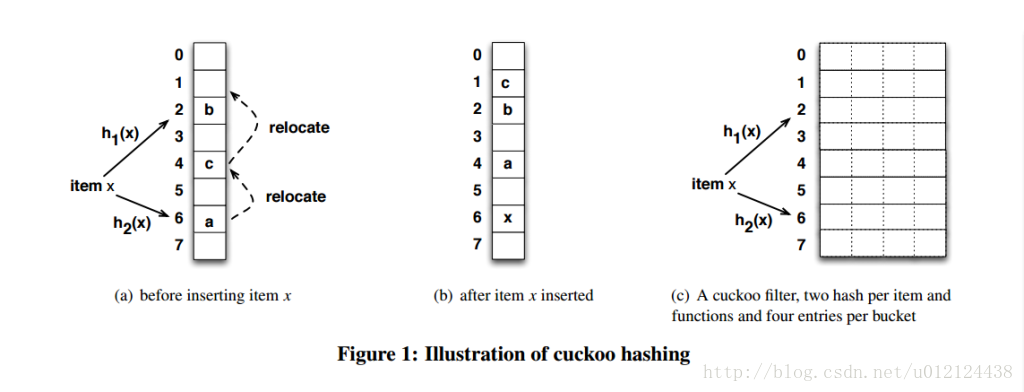
布谷鸟散列的实现
实现布谷鸟散列是需要一个散列函数的集合。因此,我们要定义一个接口来获取到这样的一个集合。
public interface HashFamily <AnyType>{
int hash(AnyType x, int which);
int getNumberOfFunctions();
void generateNewFunctions();
}
定义变量:
private static final double MAX_LOAD = 0.4;
private static final int ALLOWED_REHASHES = 1;
private static final int DEFAULT_TABLE_SIZE = 101;
private final HashFamily<? super AnyType> hashFunctions;
private final int numHashFunctions;
private AnyType[] array;
private int currentSize;
private int rehashes = 0;
private Random r = new Random();
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
我们指定表的最大负载是0.4,如果表的装填因子快要超过此限,就执行自动的表扩展。还定义了ALLOWED_REHASHES,如果替换过程执行了太长时间,他将指定我们要执行多少次再散列。在理论上ALLOWED_REHASHES可以是无限的,因为我们期望需要再散列的次数只是一个小常数。实际上,这取决于一些因素,如散列函数的个数、散列函数的质量以及装填因子,再散列可能令过程显著变慢,因此进行表扩展可能是值得的,因此进行表扩展可能是值得的,尽管这将花费空间。
初始化操作:
public CuckooHashTable(HashFamily<? super AnyType> hf){
this(hf, DEFAULT_TABLE_SIZE);
}
public CuckooHashTable(HashFamily<? super AnyType> hf, int size){
allocateArray(nextPrime(size));
doClear();
hashFunctions = hf;
numHashFunctions = hf.getNumberOfFunctions();
}
public void makeEmpty(){
doClear();
}
private void doClear(){
currentSize = 0;
for (int i = 0; i < array.length; i ++){
array[i] = null;
}
}
private void allocateArray(int arraySize){
array = (AnyType[]) new Object[arraySize];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
定义hash函数:
/**
*
* @param x 当前的元素
* @param which 选取的散列函数对应的位置
* @return
*/
private int myHash(AnyType x, int which){
int hashVal = hashFunctions.hash(x, which);
hashVal %= array.length;
if (hashVal < 0){
hashVal += array.length;
}
return hashVal;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
查询元素是否存在:
/**
* 查询元素的位置,若找到元素,则返回其当前位置,否则返回-1
* @param x
* @return
*/
private int findPos(AnyType x){
for (int i = 0; i < numHashFunctions; i ++){
int pos = myHash(x, i);
if (array[pos] != null && array[pos].equals(x)){
return pos;
}
}
return -1;
}
public boolean contains(AnyType x){
return findPos(x) != -1;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
删除元素:
/**
* 删除元素:先查询表中是否存在该元素,若存在,则进行删除该元素
* @param x
* @return
*/
public boolean remove(AnyType x){
int pos = findPos(x);
if (pos != -1){
array[pos] = null;
currentSize --;
}
return pos != -1;
}
插入元素:
/**
* 插入:先判断该元素是否存在,若存在,在判断表的大小是否达到最大负载,
* 若达到,则进行扩展,最后调用insertHelper方法进行插入元素
* @param x
* @return
*/
public boolean insert(AnyType x){
if (contains(x)){
return false;
}
if (currentSize >= array.length * MAX_LOAD){
expand();
}
return insertHelper(x);
}
具体的插入过程:
a. 先遍历散列函数集合,找出元素所有的可存放的位置,若找到的位置为空,则放入即可,完成插入
b. 若没有找到空闲位置,随机产生一个位置
c. 将插入的元素替换随机产生的位置,并将要插入的元素更新为被替换的元素
d. 替换后,回到步骤a.
e. 若超过查找次数,还是没有找到空闲位置,那么根据rehash的次数,判断是否需要进行扩展表,若超过rehash的最大次数,则进行扩展表,否则进行rehash操作,并更新散列函数集合
private boolean insertHelper(AnyType x) {
final int COUNT_LIMIT = 100;
while (true){
int lastPos = -1;
int pos;
for (int count = 0; count < COUNT_LIMIT; count ++){
for (int i = 0; i < numHashFunctions; i ++){
pos = myHash(x, i);
if (array[pos] == null){
array[pos] = x;
currentSize ++;
return true;
}
}
int i = 0;
do {
pos = myHash(x, r.nextInt(numHashFunctions));
} while (pos == lastPos && i ++ < 5);
AnyType temp = array[lastPos = pos];
array[pos] = x;
x = temp;
}
if (++ rehashes > ALLOWED_REHASHES){
expand();
rehashes = 0;
} else {
rehash();
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
1.在insertHelper过程中,通过声明一个rehashes来跟踪已经为这次插入尝试多少次再散列。
2.insert函数是相互递归的:在某些情况,insert最终调用了rehash,rehash又回头调用insert。
3.这里的insert逻辑和经典方法有些不同,我们已经检测到要插入的项不是已经存在的。我们检测要插入的位置是否为空,如果是,则直接插入该位置,否则再产生随机数位置pos ,但产生的位置不能与原来的位置相同,把元素放入pos ,如果pos 原本有元素,则将原本的元素再hash,插入到新的位置。
扩表和rehash操作:
private void expand(){
rehash((int) (array.length / MAX_LOAD));
}
private void rehash(){
hashFunctions.generateNewFunctions();
rehash(array.length);
}
private void rehash(int newLength){
AnyType [] oldArray = array;
allocateArray(nextPrime(newLength));
currentSize = 0;
for (AnyType str : oldArray){
if (str != null){
insert(str);
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
expand函数将创建一个更大的数组,但是保持用同样的散列函数。零参数的rehash函数保持数组规模不变,但创建一个新的数组,用新选的散列函数去填充。
进行测试:
public class CuckooHashTableTest {
private static HashFamily<String> hashFamily = new HashFamily<String>() {
@Override
public int hash(String x, int which) {
int hashVal = 0;
switch (which){
case 0:{
for (int i = 0; i < x.length(); i ++){
hashVal += x.charAt(i);
}
break;
}
case 1:
for (int i = 0; i < x.length(); i ++){
hashVal = 37 * hashVal + x.charAt(i);
}
break;
}
return hashVal;
}
@Override
public int getNumberOfFunctions() {
return 2;
}
@Override
public void generateNewFunctions() {
}
};
public static void main(String[] args){
CuckooHashTable<String> cuckooHashTable = new CuckooHashTable<String>(hashFamily, 5);
String[] strs = {"abc","aba","abcc","abca"};
for (int i = 0; i < strs.length; i ++){
cuckooHashTable.insert(strs[i]);
}
cuckooHashTable.printArray();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
优化(减少哈希碰撞):
1、将一维改成多维,使用桶(bucket)的4路槽位(slot);
2、一个key对应多个value;
3、增加哈希函数,从两个增加到多个;
4、增加哈希表,类似于第一种;
跳房子散列
跳房子散列概述
跳房子散列是线性探测法的改进,久的线性探测法,表的约接近满,插入冲突次数就会增加,这样插入操作的复杂度就会变高,跳房子散列出现就是为了降低冲突次数。
跳房子散列的思路
跳房子散列的思路是用事先确定的 对计算机底层体系结构而言是最优秀的一个常数 给探测序列的最大长度加一个上届。这样做可以给常数的最坏查询时间,并且与布谷鸟散列一样,查询并优化,以同时检查可用位置的有限集。
如果某次插入要把一个新的项放到距离它的散列位置太远的地方,我们会很有效的掉头想散列位置走,替换掉潜在项,如果足够谨慎,那么替换可以很快完成,并且保证那些被替换的想都不会放到距离它们的散列位置很远的地方。
跳房子散列的大致步骤
首先对key进行hash得到桶的下标i。
1.如果下标为i的桶是空的,则插入key到桶中,然后返回。
2.如果不为空,则从i开始线性探测,直到找到一个空闲的桶,下标为j
3.如果j距离i在H-1范围内,则把key插入到桶中然后返回,否则认为j远离了i,为了找到一个离i近的,空闲的桶,需要找到一个桶在i和j之间并且距离j在H-1范围内,然后把j替换成y,这个时候y所在的位置就空闲起来了,这个时候再查看y是否距离i在H-1范围内,如果不在就继续步骤3直到找到一个符号条件的就把key插入到桶中,如果最终没有找到就进行hash table扩容。
跳房子散列实现
1.创建项目元素类,存储每个位置的值与距离标志
public class HashItem <T>{
private T value;
private int dist;
public HashItem(T value)
{
this.value = value;
}
public T getValue() {
return value;
}
public void setValue(T value) {
this.value = value;
}
public int getDist() {
return dist;
}
public void setDist(int dist) {
this.dist = dist;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
2.跳房子散列具体实现
package com.example.datastruct.charpter4.hashcode;
public class HopScotchHashTable<T> {
public class HashItem <T>{
private T value;
private int dist;
public HashItem(T value)
{
this.value = value;
}
public T getValue() {
return value;
}
public void setValue(T value) {
this.value = value;
}
public int getDist() {
return dist;
}
public void setDist(int dist) {
this.dist = dist;
}
}
private HashItem<T>[] arr;
private static final int DEFAULT_SIZE = 101;
private int eleSize;
private static final double MAX_LOAD = 0.5;
private static final int MAX_DIST = 4;
public HopScotchHashTable(int size)
{
arr = new HashItem[size];
for(int i = 0; i < arr.length; i++)
{
arr[i] = new HashItem<T>(null);
}
eleSize = 0;
}
public HopScotchHashTable()
{
this(DEFAULT_SIZE);
}
public void print()
{
T value = null;
for(HashItem<T> item : arr)
{
value = item.getValue();
if(value != null)
{
System.out.println(value);
}
}
}
public boolean contains(T value)
{
return findPos(value) != -1;
}
private int findPos(T value)
{
int hash = myhash(value);
for(int i = 0; i < MAX_DIST; i++)
{
int dist = arr[hash].getDist();
if((dist >> i) % 2 == 1)
{
if(arr[hash + MAX_DIST - 1 - i].getValue().equals(value))
{
return hash + MAX_DIST - 1 - i;
}
}
}
return -1;
}
public void remove(T value)
{
int pos = findPos(value);
int hash = myhash(value);
if(pos != -1)
{
arr[pos].setValue(null);;
arr[hash].setDist(arr[hash].getDist() - (1 << (MAX_DIST - 1 - pos + hash)));
eleSize--;
}
}
public void insert(T value)
{
if(eleSize >= (int)(arr.length * MAX_LOAD))
{
rehash();
}
insertHelper(value);
}
private void insertHelper(T value)
{
while(true)
{
int pos = myhash(value);
int temp = pos;
while(arr[pos].getValue() != null)
{
pos++;
}
if(pos <= temp + MAX_DIST - 1)
{
arr[pos].setValue(value);
arr[temp].setDist(arr[temp].getDist() + (1 << (MAX_DIST - 1 - pos + temp)));
eleSize++;
return;
}
while(true)
{
boolean isNotDist = false;
for(int i = MAX_DIST - 1; i > 0; i--)
{
for(int j = MAX_DIST - 1; j > MAX_DIST - 1 - i; j--)
{
if((arr[pos - i].getDist() >> j) % 2 == 1)
{
HashItem<T> item = arr[pos - i + MAX_DIST - 1 - j];
arr[pos].setValue(item.getValue());
item.setDist(item.getDist() - (1 << j) + 1);
pos = pos - i + MAX_DIST - 1 - j;
if(pos <= temp + 3)
{
arr[pos].setValue(value);
arr[temp].setDist(arr[temp].getDist() + (1 << (MAX_DIST - 1 - pos + temp)));
eleSize++;
return;
}
else
{
isNotDist = true;
break;
}
}
}
if(isNotDist)
{
break;
}
}
if(!isNotDist)
{
break;
}
}
rehash();
}
}
private void rehash()
{
HashItem<T>[] oldArr = arr;
arr = new HashItem[(int)(arr.length / MAX_LOAD)];
for(int i = 0; i < arr.length; i++)
{
arr[i] = new HashItem<T>(null);
}
eleSize = 0;
for(HashItem<T> item : oldArr)
{
if(item.getValue() != null)
{
insert(item.getValue());
}
}
}
private int myhash(T value)
{
int hash = value.hashCode();
hash %= arr.length;
if(hash < 0)
{
hash += arr.length;
}
return hash;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
可扩散列
可扩散列是继B树以来又一个复杂的数据结构,难点是树叶分裂。
分裂的思路:
首先判断当前dl是否小于目录D;
如果小于,不用倍增目录。要让这一个分开指向两片树叶。一半(左边),一半(右边)分别指向一片树叶。注意dl可能小于D不只1,所以就要判断一半的数量是多少。
等于的话。就要倍增目录。这种情况相对前者很简单。


























 3423
3423

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








