一、什么是动态规划算法
动态规划一般也只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,
故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
动态规划算法分以下4个步骤:
1,描述最优解的结构
2,递归定义最优解的值
3,按自底向上的方式计算最优解的值 //此3步构成动态规划解的基础。
4,由计算出的结果构造一个最优解。 //此步如果只要求计算最优解的值时,可省略。
动态规划的两个最重要性质:最优子结构性质,和子问题重叠性质。
A, 最优子结构
如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。意思就是,总问题包含很多个
子问题,而这些子问题的解也是最优的。
B,重叠子问题
子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法
正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,
只是在表格中简单地查看一下结果,从而获得较高的效率。
二、LCS问题
问题描述:
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说,若给定序列X=<x1, x2,…, xm>,则另一序列Z=<z1, z2,…, zk>是X的子序列
是指存在一个严格递增的下标序列 <i1, i2,…, ik>,使得对于所有j=1,2,…,k 有Xij=Zj;例如,序列Z=<B,C,D,B>是序列X=<A,B,C,B,D,A,B>的子序列,相应
的递增下标序列为<2,3,5,7>。
给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。例如,若X=<A, B, C, B, D, A, B>和Y=<B, D, C, A, B, A>,
则序列<B, C, A>是X和Y的一个公共子序列,序列<B, C, B, A>也是X和Y的一个公共子序列。而且,后者是X和Y的一个最长公共子序列,因为X和Y没有长度大
于4的公共子序列。
最长公共子序列(LCS)问题:给定两个序列X=<x1, x2, …, xm>和Y=<y1, y2, … , yn>,要求找出X和Y的一个最长公共子序列。
问题分析:
最长公共子序列的结构
最长公共子序列的结构有如下表示:
设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>,则:
1,若xm=yn,则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列;
2,若xm≠yn且zk≠xm ,则Z是Xm-1和Y的最长公共子序列;
3,若xm≠yn且zk≠yn ,则Z是X和Yn-1的最长公共子序列。
其中Xm-1=<x1, x2, …, xm-1>,Yn-1=<y1, y2, …, yn-1>,Zk-1=<z1, z2, …, zk-1>。
子问题的递归结构:
由最长公共子序列问题的最优子结构性质可知,要找出X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列,可按以下方式递归地进行:
当xm=yn时,找出Xm-1和Yn-1的最长公共子序列,然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。当xm≠yn时,必须解两个子
问题,即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。
由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如,在计算X和Y的最长公共子序列时,可能要计算出X和Yn-1及Xm-1和Y的
最长公共子序列。而这两个子问题都包含一个公共子问题,即计算Xm-1和Yn-1的最长公共子序列。
我们来建立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>,Yj=<y1, y2, …, yj>。当i=0或j=0时,
空序列是Xi和Yj的最长公共子序列,故c[i,j]=0。其他情况下,由定理可建立递归关系如下:
计算最优值:
直接利用上节节末的递归式,我们将很容易就能写出一个计算c[i,j]的递归算法,但其计算时间是随输入长度指数增长的。由于在所考虑的子问题空间中,
总共只有θ(m*n)个不同的子问题,因此,用动态规划算法自底向上地计算最优值能提高算法的效率。
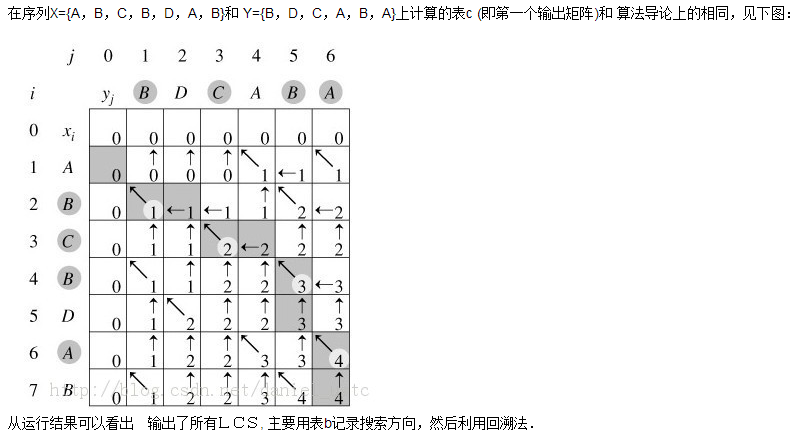
计算最长公共子序列长度的动态规划算法Lcs(X,Y)以序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>作为输入。输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。
其中c[i,j]存储Xi与Yj的最长公共子序列的长度,b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的,这在构造最长公共子序列时要用到。最后,X和Y的
最长公共子序列的长度记录于c[m,n]中。
用回溯法来找到最优解,nlcs表示最优值.
以下为代码:
// multiplication.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <iostream>
using namespace std;
const int maxSize = 100;
int c[maxSize][maxSize];//记录序列x和y的LCS的长度
int b[maxSize][maxSize];
char lcs[maxSize];//记录LCS字符
int nlcs = 0;//记录LCS最大长度
int Lcs(char *x, char *y)
{
int lenX = strlen(x) - 1;
int lenY = strlen(y) - 1;
int i, j;
for (i = 0; i <= lenX; i++)//将c[][]初始化,至零
{
memset(c[i], 0, sizeof(int)*lenY);
}
for (i = 1; i <= lenX; i++)
for (j = 1; j <= lenY; j++)
{
if(x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 1;//对角线方向
}
else if ( c[i-1][j] > c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 2;//正上方
}
else if (c[i-1][j] < c[i][j-1])
{
c[i][j] = c[i][j-1];
b[i][j] = 3;//左方
}
else
{
c[i][j] = c[i - 1][j];
b[i][j] = 4;//左、上方
}
}
return c[lenX][lenY];
}
/*
功能:回溯法递归输出所有的LCS
说明:
X:一个序列
curlen:记录当前LCS的长度
i,j:待搜索的下标,初始值为两个序列的长度
*/
void print_all(char *x,int curlen, int i, int j)
{
if(i<0 || j<0)
return ;
static int len =0;
//如果当前lcs的长度等于已知的LCS的长度则输出子序列
if(len == nlcs)
{
for(int k=nlcs-1; k>=0; k--)
printf("%c ", lcs[k]);
printf("\n");
}
else
{
if(b[i][j] ==1)
{
lcs[curlen] = x[i];
len++;//子序列长度加1
print_all(x,curlen+1,i-1,j-1);//沿对角线方向搜索
len--;//回溯
}
else if(b[i][j] ==2)
print_all(x,curlen,i-1, j);
else if(b[i][j] ==3)
print_all(x,curlen,i,j-1);
else//b[i][j] ==4 递归调用 沿上、左两个方向搜索
{
print_all(x,curlen,i,j-1);
print_all(x,curlen,i-1, j);
}
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int i, j;
char x[maxSize] = {' '}, y[maxSize] = {' '};
cout << "enter X arr: ";
cin >> x + 1;
cout << "enter y arr: ";
cin >> y + 1;
int lx = strlen(x) - 1, ly = strlen(y) - 1;
nlcs = Lcs(x, y);
cout<<"序列X和Y的所有子序列的LCS长度矩阵:" <<endl;
for (i = 0; i<=lx; i++)
{
for (j = 0; j <= ly; j++)
{
cout<< c[i][j] << " ";
}
cout << endl;
}
cout<<"搜索方向标记矩阵,1-对角线方向;2-向上;3-向左;4-向上或向左:" <<endl;
for (i = 0; i<=lx; i++)
{
for (j = 0; j <= ly; j++)
{
cout<< b[i][j] << " ";
}
cout << endl;
}
cout <<"最长公共子串长度为: "<< nlcs <<endl;
cout <<"所有最长公共子串: ";
print_all(x, 0, lx, ly);
return 0;
}
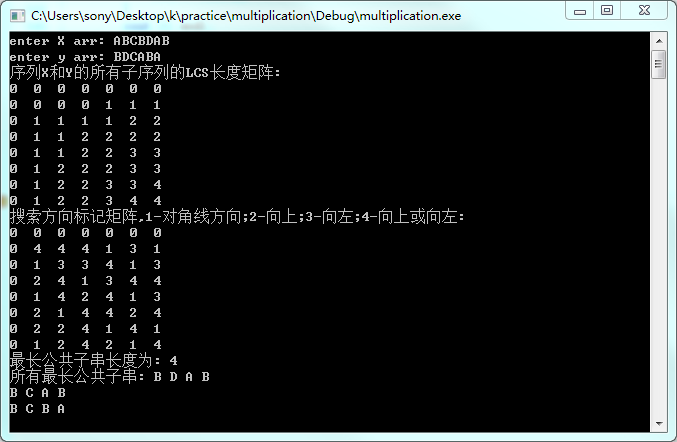
结果图如下:








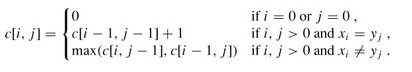














 1082
1082

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








