转载链接:http://blog.csdn.net/kangroger/article/details/39254619
约瑟夫环问题:一圈共有N个人,开始报数,报到M的人自杀,然后重新开始报数,问最后自杀的人是谁?
如图:内环表示人排列的环,外环表示自杀顺序;上面N=41,M=3。
最普通办法就是模拟整个过程:建一个bool数组,true表示此人还活着,false表示已经自杀。可以模拟整个过程
- #include<iostream>
- using namespace std;
- int main()
- {
- int N;//人的总个数
- int M;//间隔多少个人
- cin>>N;
- cin>>M;
- bool *p=new bool[N+1];//[1……N]为true表示此人还活着
- for (int i=1; i <= N; i++)
- *(p+i)=true;
- int count=0;//统计自杀的人数
- for (int i=1, j=0; ;i++)//i用来表示循环,j用来计算是不是第N个人
- {
- if (*(p+i))//此人还活着
- {
- j++;
- if (j == M)
- {
- *(p+i)=false;
- j=0;
- count++;//统计自杀的人
- }
- if (count == N)
- {
- cout<<"最后自杀的人是:"<<i<<endl;
- break;
- }
- }
- if(i == N)
- i=0;
- }
- delete []p;
- return 0;
- }
把问题重新描述一下:N个人(编号0~(N-1)),从0开始报数,报到(M-1)的自杀,剩下的人继续从0开始报数。求最后自杀者的编号。
N个人编号如下:
第一个自杀的人是(M-1)%N,例如上图中,41个人中,报道3的人自杀,则字一个自杀的人的编号是(3-1)%41=2。编号(M-1)%N自杀后,剩下的人排列如下:
有人自杀后,下一个位置M又从零开始报数,因此环应该如下:
将上面的排列顺序重新编号:
问题变为(N-1)个人,报道为(M-1)的人自杀,问题规模减小了。这样一直进行下去,最后剩下编号为0的人。用函数表示:
F(1)=0
当有2个人的时候(N=2),报道(M-1)的人自杀,最后自杀的人是谁?应该是在只有一个人时,报数时得到的最后自杀的序号加上M,因为报到M-1的人已经自杀,只剩下2个人,另一个自杀者就是最后自杀者,用函数表示:
F(2)=F(1)+M
可以得到递推公式:
F(i)=F(i-1)+M
因为可能会超出总人数范围,所以要求模
F(i)=(F(i-1)+M)%i
有了递推公式就可以在O(N)时间求出结果:
- #include<iostream>
- using namespace std;
- int main()
- {
- int N;//人的总个数
- int M;//间隔多少个人
- cin>>N;
- cin>>M;
- int result=0;//N=1情况
- for (int i=2; i<=N; i++)
- {
- result=(result+M)%i;
- }
- cout<<"最后自杀的人是:"<<result+1<<endl;//result要加1
- return 0;
- }
-









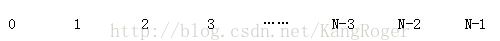

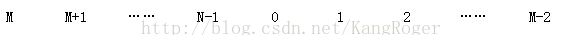
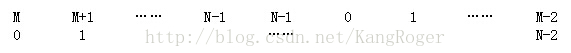














 7642
7642

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








