概论_真题讲解

题1

设在15只同类型零件中有2只为次品，在其中取3次， 每次任取1只， 作不放回抽样， 以 X 表示取出的次品个数， 求：

（1）X的分布律；（2）X的分布函数并作图； （3）P{X≤0.5}，  P{1<X≤1.5},  P{1≤X≤1.5}, 

  P{1<X<2}.

解：

注意： 分布函数作图是比较简单的， 解答出来是为了解决对 概率论作图 感到陌生的问题，

当画出图后，就明白怎么回事，怎样去作图了。

要特别注意区分： F(2)  ≠  P{X=2}

因为F(2)=P{x≤2} ,  这个值一般是大于P{X=2},  也就是说 P{X≤2} > P{X=2}, 

P{X=2}只是一个点的概率值，  P{X≤2}  却是数轴上从 -∞ 到2 很长一段的概率值！！

题2

 题 3

将3只球随机地放入4个杯子中去， 求杯子中球的最大个数分别为1， 2， 3的概率。

解： 此题乍一看，可能有点懵,  是从球的角度出发 还是  从杯子的角度出发?

我想说：我们不要怕复杂， 有的人一看到这类型题， 就发怵，就害怕， 因为不会不懂，

没什么要怕的！ 越是复杂越要沉着应对， 越要静下心来学， 越要掌握！！！

~~~~~

本题，每个杯子的容量不限，第1个球有4种放法(不存在不放进任何杯子的情况），第2个球有4种放法，第3个球有4种放法， 也就是说只存在有的杯子没球。

 总共的放法为N(S) = 4 x 4 x 4 =64.   这是样本空间的总数，清楚这点是关键。

设事件A为杯子中球的最大个数为1，3个球要往4个杯子里面放，

第一步 就是从4个杯子选出3个杯子，为，

第二步 选好了杯子，就要放球进去，第1个球有3种放法，第2个球只有2种放法， 第3个球只有1种放法。

所以事件A的放法为：=24， P(A) = .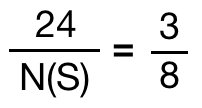

设事件B为杯子中球的最大个数为2， 3个球要往4个杯子里面放，虽然实际上只放到2个杯子中，

第一步  从4个杯子先选出放2个球的杯子，为 4种，再选出放1个球的杯子，为3种

第二步  开始放球进去，要放2个球的杯子放球有 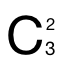=3种放法；  放1个球的杯子，只能从3个球选走2个球后的1个球，放进去，只有1种放法。

所以事件B的放法 4x3x3x1 = 36.  P(B) =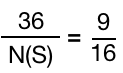 

设事件C为杯子中球的最大个数为3，   3个球要往4个杯子里面放，虽然实际上只放到1个杯子中，

第一步  从4个杯子选出放3个球的杯子，为4种；

第二步  开始放球进去，要放3个球的杯子放球只有1种；  

所以事件C的放法 4x1 = 4.  P(C) = 

结论：  杯子中球的最大个数为1的概率为3/8, 

            杯子中球最大个数为2的概率为9/16, 

            杯子中球最大个数为3的概率为1/16.

题4

设随机变量X的密度函数为  

，对X进行三次独立重复观测， Y表示三次独立重复观测中事件{X<   }出现的次数， 求P{Y1}

解： Y出现的次数 可能为 0， 1，2，3.  Y符合二项分布。

         P{X<  } = ，

        三次独立重复的事件{X<  }出现的次数 Y~B(3, )

       P{Y1} = 1 - P{Y=0} = 1-  =  1 -  =  

  题目4涉及到离散型也涉及到连续型，具有代表性，是一个很适合考试的题目。

题 5  2014.4  分值10分   关于二项分布

某产品的次品率为0.1， 检验员每天抽检 10 次， 每次随机取 3 件 产品进行检验， 且不存在误检现象， 设产品是否为次品相互独立，  若在一次检验中检出次品多于 1 件，  则调整设备， 以 X 表示一天调整设备的次数，  求  E(X)

解：  本题，要审清题意， 每天10次， 每次取3件检验，

在每次检验中， 属于独立重复实验， 为二项分布， 设Y为每次检验检出次品的分布，有

Y ~ B(3,  0.1) ,

P{Y > 1} = 1- P{Y=0}- P{Y=1} = 1- ,  

所以 X ~ B(10, 0.028),  E(X) = np = 10 * 0.028 = 0.28.

总结： 本题要清楚 X 事件的含义， X也是独立重复实验， 触发 X 事件就要先得出 概率。