Python算法——求集合的所有子集

要求：

       有一个集合，求其全部子集(包含集合自身)。例如集合[1,2,3]其全部子集为：<∅,1,2,12,3,13,23,123>

分析：

       方法一：位图法

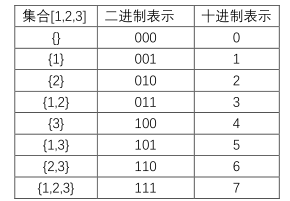
       ①使用两层循环，外层循环为子集个数，对于集合长度为N，子集个数为。外层循环每循环一次一个子集。内层循环用来判断二进制下标为i的位置数是否为"1"，如果对应位为1，那么就输出这个位，如果对应位为0，那么不输出这个位。

       ②以集合[1,2,3]为例，N = len([1,2,3])，外层循环 i 取值范围为[0,7]，内层循环用于判断 i 对应二进制下标为j的位置是否为1。如果 (i >>j)%2为真，那么输出此子集。

       ③当 i =0时，无论 i 对应二进制000右移0位，1位，还是2位，即(i>>j)%2始终为0(假)，输出空集。

      ④当 i =1时， i 对应二进制001右移0位，即(i>>j)%2为1(真)，输出[1]。 i 对应二进制001右移1位为000，即(i>>j)%2为0(假)，不追加。 i 对应二进制001右移2位为000，即(i>>j)%2为0(假)，不追加。最终输出[1]。

       ......

     ⑤当 i = 3时，i 对应二进制011右移0位，即(i>>j)%2为1(真)，输出[1]。 i 对应二进制011右移1位为001，即(i>>j)%2为1(真)，追加输出[1,2]。 i 对应二进制011右移2位为000，即(i>>j)%2为0(假)，不追加。最终输出[1,2]。

       ......

    ⑥当 i = 6时，i 对应二进制110右移0位，即(i>>j)%2为0(假)，输出[]。 i 对应二进制110右移1位为011，即(i>>j)%2为1(真)，追加输出[2]。 i 对应二进制110右移2位为001，即(i>>j)%2为1(真)，追加输出[2,3]。最终输出[2,3]。

    ⑦当 i = 7时，i 对应二进制111右移0位，即(i>>j)%2为1(真)，输出[1]。 i 对应二进制111右移1位为011，即(i>>j)%2为1(真)，追加输出[1,2]。 i 对应二进制111右移2位为001，即(i>>j)%2为1(真)，追加输出[1,2,3]。最终输出[1,2,3]。

       方法二：迭代法

       假设原始集合s = [1,2,3]，

       第一次迭代：<1>;

      第二次迭代：<1,12,2>;

      第三次迭代：<1,12,2,13,123,23,3>;

      每次迭代，都是上一次迭代的结果+上次迭代结果中每个元素都加当前迭代元素+当前迭代元素

实现代码：

#方法一
def PowerSetsBinary(items):
    N = len(items)
    for i in range(2 ** N): #子集个数，每循环一次一个子集
        combo = []
        for j in range(N): #用来判断二进制下标为j的位置数是否为1
            if(i>>j)%2:
                combo.append(items[j])
        print(combo)

PowerSetsBinary([1,2,3])

       运行结果：

[]
[1]
[2]
[1, 2]
[3]
[1, 3]
[2, 3]
[1, 2, 3]

#方法二
def getAllSubset(str):
    if str == None or len(str) < 1:
        print("参数不合理！")
        return None
    arr = []
    arr.append(str[0:1]) #str首元素
    i = 1
    while i < len(str):
        lens = len(arr)
        j = 0
        while j < lens:
            arr.append(arr[j]+str[i])
            j += 1
        arr.append(str[i:i+1])
        i += 1
    return arr

if __name__ == "__main__":
    result = getAllSubset("123")
    i = 0
    while i < len(result):
        print("["+result[i]+"]")
        i += 1

       运行结果：

[1]
[12]
[2]
[13]
[123]
[23]
[3]

性能分析：

       方法二第k次迭代的迭代次数为。需要注意的是，1≤k≤n，迭代n次，总的遍历次数为：-(2+n)，n≥1，所以此方法时间复杂度为O()。由于该算法中，下一次迭代需要上一次迭代结果，而最后一次迭代之后就没有下一次了。因此，假设原始集合有n个元素，在迭代过程中总共需要保存的子集个数为-1,n≥1。但需要注意的是，这里只考虑子集个数，每个子集元素长度被视为1。