信息熵、条件熵、信息增益

信息增益描述了一个特征带来的信息量的多少，往往用于特征选择

信息增益 = 信息熵 - 条件熵

一个特征往往会使一个随机变量Y的信息量减少，减少的部分就是信息增益

一个例子

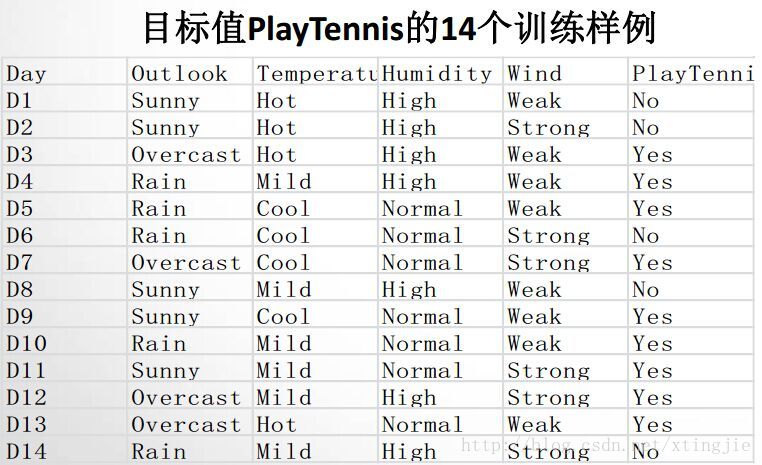
如图所示，目标值是：playtennis，也就是是否打球
有四个特征：天气、温度、湿度、风

信息熵

信息熵的公式：
$H(X)=-\sum\limits_{i=1} ^{n} p(x_i)\log p(x_i)$
以上图为例，设是否打球这一随机变量为Y，则

$p(y=yes)=\frac{5}{14}$

$p(y=no)=\frac{9}{14}$

所以$H(Y)=-\frac{5}{14}*log(\frac{5}{14})-\frac{9}{14}*log(\frac{9}{14})=0.6518$

条件熵

条件熵表示在条件X下Y的信息熵。公式如下：

$H(Y|X)=\sum\limits_{x\in X}p(x)H(Y|X=x)$

在上图的例子中，设humidity湿度为随机变量X

则，p(x=high)=7/14=1/2=p1

p(x=normal)=7/14=1/2=p2

所以，H(Y|X)=p1*H(Y|X=high)+p2*H(Y|X=normal)

而接下来就是计算H(Y|X=high)和H(Y|X=normal)

根据信息熵的计算方法可以得出：

H(Y|X=high)=-4/7*log(4/7)-3/7*log(3/7) = 0.6829
H(Y|X=normal)=-1/7*log(1/7)-6/7*log(6/7) = 0.4101

因此，条件熵为：1/2*0.6829+1/2*0.4101=0.5465

信息增益

信息增益 = 信息熵 - 条件熵=0.6518-0.5465=0.1053
也就是说，引入了湿度humidity这个变量之后，就使得是否打球这个变量的信息量就从0.6518减小到了0.5465
信息量是描述变量的不确定性的，值越大，就表示这个事件越不确定
因此，湿度这个变量的引进，使得这种不确定性降低了，有利于做决定

信息增益常用于决策树的构建，和特征选择