一、 缘起
之前根据目前所学(看《游戏编程中的人工智能》以及网上的各种博客文章等等资料),写了一篇关于神经网络实现手写数字识别的文章,但随着继续学习(尤其是后来报了CSDN的《机器学习:机器学习40天精英计划》课程),发觉之前的文章对反向传播以及神经网络的演化(或者说学习)论述的还很牵强,不够到位,于是就想着再次整理一下关于反向传播相关的知识,就权当做学习笔记吧。
二、分解神经元(人工神经细胞)
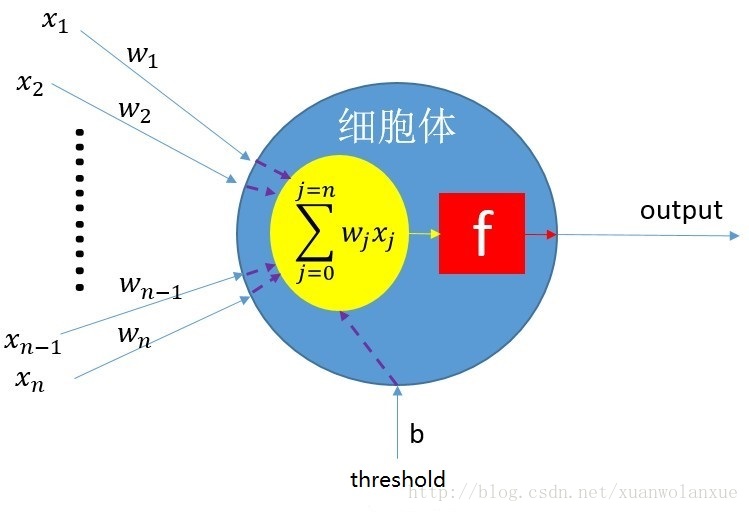
前面《神经网络实现手写数字识别(MNIST)》一文中展示了一个人工神经细胞的模型结构图,如下所示:
从上图中可以看出一个人工神经细胞其实是由多个函数复合而成的,详细一点的分解就是如下所示:
以很色竖线为界,左边为上面人工神经细胞模型的黄色部分:
右边部分就是人工神经细胞的激活函数部分:
如果将两个公式合二为一可以写为:
三、数学原理
3.1 偏导数
在百度百科中对偏导数的解释为:
在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。偏导数在向量分析和微分几何中是很有用的。
比如这里有个二元函数 z=f(x,y)
如果要求在 (x0,y0) 处对x的偏导,就需要将y固定在 y0 处,将其看着常数,这个时候二元函数也就可以看做一个一元函数 z=f(x,y0) ,然后就可以求出 z=f(x,y0) 在 x0 处的导数,也就是 z=f(x,y) 在 (x0,y0) 处对x的偏导数
同理,将x固定 x0 处,让y有增量 △y ,如果极限存在 那么此极限称为函数 z=f(x,y) 在 (x0,y0) 处对y的偏导数。记作 f′y(x0,y0) ,也就是: ∂f∂y∣∣∣y=y0x=x0
偏导数反映的是函数沿坐标轴正方向的变化率
3.2 链式法则
在百度百科中的解释为:
链式法则(英文chain rule)是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。
然后也举了例子来说明,大概就是:
如果有这么一个复合函数 f(g(x)) ,如果此函数对x求导,根据链式法则就应该是:
其他形式: ∂y∂x=∂y∂z.∂z∂x
拿一个具体的函数来说,比如: y=sin(x2+1)
这里就是一个复合函数,
- g(x)=x2+1
- f(x)=sin(x) 既 f(g(x))=sin(g(x))
根据链式法则,对此函数求导为:
链式法则用文字描述,就是“由两个函数凑起来的复合函数,其导数等于里边函数代入外边函数的值之导数,乘以里边函数的导数
3.3 反向传播原理
简单来说,反向传播原理(或者说作用)就是,将神经细胞的输出误差反向传播到神经细胞的输入端,并以此(当然还会加上)来更新神经细胞输入端的权重。
在详细说明反向传播原理之前,需要先理解几个概念:
- 输出误差,既神经细胞的期望输出与实际输出之间的差值,其表达式为: δ=Ot−Or ,其中 Ot 为期望输出, Or 为实际输出
- 学习率,用以控制神经网络的学习速度的,实际就是用于控制神经细胞输入权重调整幅度的
接下来就来详细说说反向传播原理,如神经细胞分解一章所示,我们可以将一个神经细胞分为两个部分
其一(前半部分:累加部分):
其二(后半部分:激活部分)
现在复合函数有了,输出误差的概念也有了,那这个反向传播该如何传呢?
前面介绍了求偏导和链式法则,在这里就该是它们表演的时候了。
这里也就分成两个部分来看:
- 激活部分
从上面可以看出,激活部分是一个一元函数,其波形图如下所示:
如上图所示,假设点A就是我们期望的点,对应的y轴上的点 Ot 就是神经细胞的期望输出值,对应的x轴上的点 Xt 就是我们期望的神经细胞的累加部分能够输出的期望值。同理点B就是神经细胞实际输出点。
当一个神经细胞被激活,得到输出之后(也就是完成正向传播之后),我们将知道 Or 和 Xr 的值,又因为是训练,所以我们也会知道 Ot 的值,然后根据这些已知的值又可以计算出神经细胞的期望输出与实际输出之间的误差: δo=Ot−Or ,最后就只有 Xt 是未知的。
但是在这里,我们并不是要去求 Xt 的值,既然是要讲神经细胞的输出误差反向传播回去,那么我们要求的就是神经细胞累加部分的输出误差,也就是: δx=Xt−Xr 。
具体的要如何来求这个变化率呢?
既然前面介绍偏导的时候已经说到“偏导数反映的是函数沿坐标轴正方向的变化率”,而这里的函数是一元函数,也就是说其导数(因是一元所以就不存在“偏”)反应的就是其变化率。
所以,这里就可以使用激活部分的一元函数的导数来求解(传播)从点A到点B的变化率。
因为这里的激活部分的一元函数是sigmoid函数,所以其导数为(省略推导过程,直接看结果):
换一种形式如下:
这个函数就代表了将神经细胞输出误差反向传播回来时的变化率,其中的x就是神经细胞的实际输出 Or ,也就是说实际的输出误差 δo 乘上这个变化率就能得到反向传播回来的真实误差.因此累加部分的输出误差为:
- 累加部分
如下是一个简单的神经网络:
上图中神经绿色部分为整个神经网络的输入数据,蓝色部分为隐含层神经细胞层,红色部分为输出层神经细胞层。
这一部分和激活部分有点不一样的是,这里是一个复合函数,如下所示:
对这个函数进行第一步分解可得到:
也就是说,一个神经细胞包含n( n>=1 )个输入。所以神经细胞累加部分的输出就是这n个输入的累加和,也就是说,对于累加部分的输出,这n个输入均有各自的贡献,其程度也受到各自权重w的影响。
同理,累加部分输出的误差也是所有输入共同贡献的结果,所以在这里我们就需要使用前面介绍的“链式法则”分别对每一个输入求偏导数来获得每一个输入部分误差贡献,进而可以将误差反向传播到反向的下一层神经细胞层,也能进行权重更新。
以上面的简单神经网络为例,假如这里就是图中神经细胞“ f3(e) ”的累加部分,由图可知, f3(e) 的输入包含 f1(e) 和 f2(e) 两个神经细胞,其对应权重分别是 w5 和 w7 ,以公式表示 f3(e) 的累加部分为:
换一种形式(将 fj(e) 以 Oj 表示):
f3(e)
神经细胞的最终输出表示为:
按照链式法则的规则,如果要求神经细胞 f1(e) 对神经细胞 f3(e) 的输出误差的贡献,就可以先将神经细胞 f2(e) 的输出和对应权重固定,也就是看着一个常数,因此在求导时,这个相加的常数项就直接为0而忽略掉了,这时的函数形式变为。
换一种形式:
同理可得:
当然,这里其实仍然是一个复合函数,因为不管是 O1 还是 w5 都是变量,所以,如果我们对 O1 求偏导数,就等于是将输出误差反向传播到反向的下一层神经细胞层,如果对 w5 求偏导数,就是获得需要调整的权重w的变化量(当然这里会需要加入学习率的控制)。
具体的,对
O1
求偏导数的结果为:
对
w5
求偏导数的结果为:
因为神经细胞的复合函数是由激活部分和累加部分组成的,也就是说根据链式法则神经细胞最终的输出反向传播的输入端就是两者函数的导数乘积,即:
其中:
所以终上所述,对于神经细胞 f3(e) ,其反向传播给反向前一层的神经细胞的误差为:
神经细胞 f3(e) 反向传给 f1(e) 传给:
神经细胞 f3(e) 反向传给 f2(e) 的误差:
其中:
- δ1 : 神经细胞 f1(e) 的输出误差
- δ2 : 神经细胞 f2(e) 的输出误差
δx:神经细胞 f_3(e)$从最终输出透过激活部分反向传播到累加部分的误差:
δx=δ3∙O3r(1−O3r) ,其中: δ3=O3t−O3r 是$f_3(e)的最终输出误差
w5,w7 : 是函数 h1(O,w) 和函数 h2(O,w) 分别对 O1 和 O2 求偏导数
注意:这里神经细胞 f1(e)和f2(e) 的最终输出误差,也不仅仅只是上面的两个公式计算的结果,由上面的网络结构图可以看出,这两个神经细胞的输出值不但对 f3(e) 有贡献,也同样对 f4(e) 有贡献。所以 f1(e)和f2(e) 的最终输出误差为:
δ1=δ1 from f3(e)+δ1 from f4(e) δ2=δ2 from f3(e)+δ2 from f4(e)
同理可得神经细胞 f3(e) 的两个输入权重的变化量为:
其中:
- δx :和上面一样
- η :学习率,控制神经网络学习速度(或者说权重更新幅度)的系数
接下来就是在原有的权重基础上对权重进行调整了。先来看一下神经网络的正向传播过程,在累加部分,因为是所有输入相加,所以权重值越大,最后得到的累加和也就越大。而在激活部分,从上面的sigmoid函数波形图可以看出,也是输入越大输出就越大。也就是说整个神经细胞的输出与权重之间近似于“单调递增”关系。
在前面我们计算神经细胞最终的输出误差时,使用的是 误差=期望值−实际值 ,期望值是训练神经网络时输入的标签,是不变的。 所以要想误差最小,就必须增大实际值去逼近期望值。而前面我们得出了神经细胞的输入权重与最终输出(即实际值)是“单调递增”的关系,也就是要增大输入权重。所以新权重 w′5和w′7 的值为:
注意:上面说,因为定义的误差公式为: 误差=期望值−实际值 ,所以要使用 + δw ,可能有的人会说,如果“实际值” 大于了“期望值” 怎么办呢?
这个没有关系,如果如果“实际值” 大于了“期望值”了,那这个“误差” 必然也是负值,而这个 + δw ,其实就相当于 − |δw| ,也就是说相当于减小权重值,也能让实际值逐渐逼近期望值
四、总结
以上是以直观的方式分析神经细胞的输入权重该如何更新调整(也就是反向传播训练神经网络的过程),其实一般都是以“梯度下降法”来分析的。但是笔者对这一块不太熟悉,网上搜索了很久,基本上都是说,使用梯度下降法,然后啪啪的拿出一堆公式,也不说明,神经网络的梯度是啥? 与权重更新这些有啥关系,这个“下降”是如何下降的? 几乎都是说就是沿着梯度下降的方向如何如何,有些不知所云。暂且就这样吧,后续如果这块搞明白了再单独写一篇梯度下降的内容或者更新到本篇内容当中。


























 1388
1388

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








