本总结是是个人为防止遗忘而作,不得转载和商用。
本节的前置知识是我总结的“推荐系统 - 1、2”。
LMF
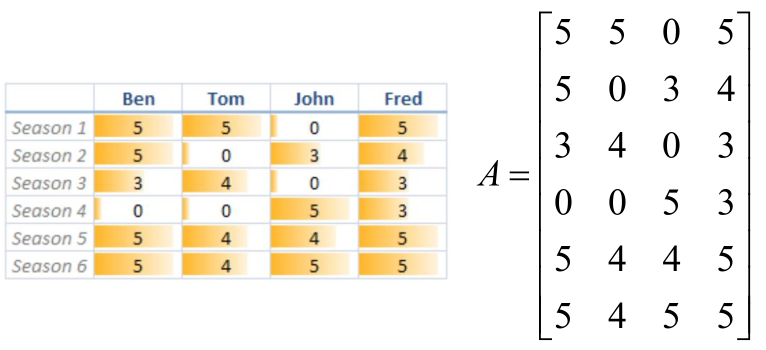
假设一个场景:假定Ben、Tom、John、Fred对6种商品进行了评价,评分越高代表对该商品越喜欢。0表示未评价,如下图:
左图是评价情况,右图是将左图写成矩阵A6*4的样子。
然后就该思考了,这些评价的标准是什么?单纯的“这个商品好”是不行的,一定是有导致“这个商品好”的原因,如:商品的产地、商品的材质等。而这个原因就是隐变量。
那基于此我们就需要建立模型,即:A分解成2个矩阵U和V,分解后如下:
Am*n= Um*k·Vk*n,K是隐变量数目
为了方便写代码,把上式改成
Am*n= Um*k·VTn*k,K是隐变量数目
进一步,建立目标函数:
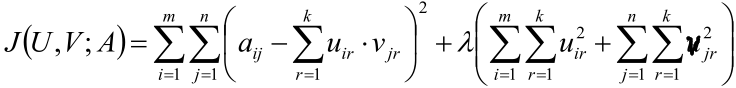
之后就是“求梯度->梯度下降”那一套了,这里再给出求导后的结果:
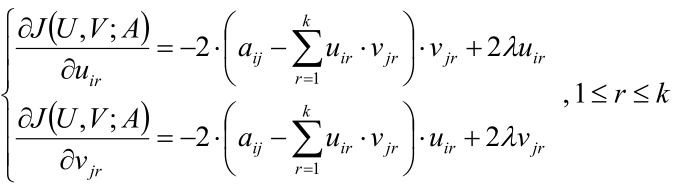
剩下的就是写代码不停地对U、V梯度下降,最后就求出U和V了。
代码(源自邹博老师)

结果(源自邹博老师)
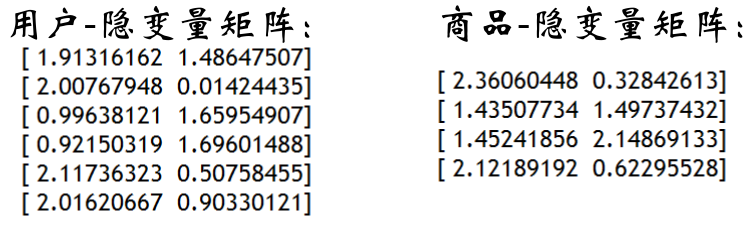
K=2时:
如上图所示,这是求出的U和V,接着把这两个矩阵点乘,就得到下面的预测矩阵:

还记得矩阵A的样子吗?里面是有一些0值的,于是这个矩阵中对应A的0的元素就是我们估计的用户对该商品的评价。
PCA(主成分分析)
实际问题往往需要研究多个特征,而这些特征存在一定的相关性。那这样一来,我们何不在所有的特征中挑选出几个有代表性的特征来表述这所有的特征呢?只要挑选的特征足够好,那即能够代表原始特征的绝大多数信息,又能使组合后的特征又互不相关,降低相关性。
而这样的操作就是主成分分析(从一样本集合中提取出主成分,并通过对主成分的分析来作为原始样本集合的分析)。
说人话就是:有一个矩阵A,我们想对A做降维,用降维后的矩阵近似表达A。
那如何找出一个合适的方法,从而既可以对A做降维,又可以让降维后的矩阵尽可能的接近于A呢?
了解SVD的可能一瞬间就想到SVD,不过主成分分析的做法不一样,主成分分析的做法是这样。
对于矩阵A=(a1,a2, ..., am),其中ai是n维的,即ai=(ai1, ai2, ..., ain),于是乎A是m*n的。一般m>n。
降维步骤:
1,令B = AT·A,这时B是个n*n的对称方阵(对称阵的特征值是实数,特征向量正交)。
2,用QR分解求B的特征值λ1,λ2, ..., λn和特征向量u1, u2,..., un。
3,造一个矩阵U=( u1,u2, ..., un)n*n,因为u1,u2, ...un正交,所以U正交,所以U·UT = I,即UT = U-1。
4,造一个对照阵∧,对角线上的元素是(λ1,λ2, ..., λn),其他都是0。
5,这时B = AT·A = UT·∧·U
6,因为如果从∧中把最小的λj去掉后是仍能保证和原始的矩阵A十分相似的,所以同理:把最小的几个λj去掉对原始矩阵A的影响不太大,即:我只保留最大的k个λ对原始矩阵A的影响不太大。
因此∧中和U中仅保留前k大的λ和u。
7,于是乎把Am*n这个n维的矩阵降维成了k维,即:
原始:ATm*n·Am*n= UTm*n·∧n*n·Um*n
降维:ATm*k·Am*k= UTm*k·∧k*k·Um*k
AT·A被称为散列矩阵。
注:PCA要求数据是高斯分布。
PCA的作用
对数据降维、去噪
PCA与SVD
还是那句话:了解SVD的可能一瞬间就想到SVD,因为PCA也是取前k个特征值对原始矩阵降维。那PCA与SVD是什么关系呢?看下面的分析:
1,对于m*n的矩阵A,其特征值和特征向量的式子是:
(AT·A)vi=λivi
2,做如下操作
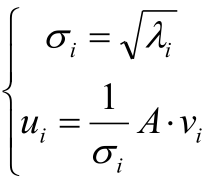
注意:因为A是m*n的,所以vi是n维的,即n*1的,所以A·vi就是m*1的,所以ui是m维的。
3,把u1, u2,..., um用U表示,σ1,σ2, ..., σn写成对角阵∑,于是A=U∑VT,这就是奇异值分解SVD的式子,推导如下:
所以LMF中的例子用SVD做的话就是:
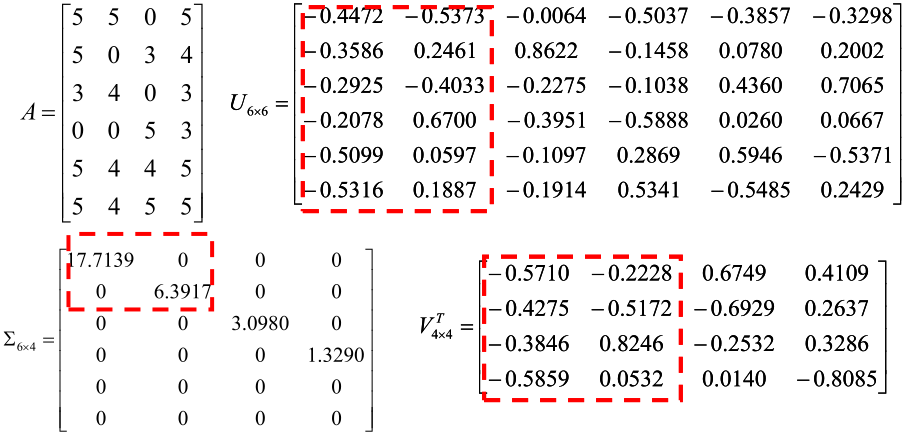
对矩阵A做SVD,然后令K=2时,有下图:
于是将U只取前两列并画图后就得到了产品的相似度,如下:
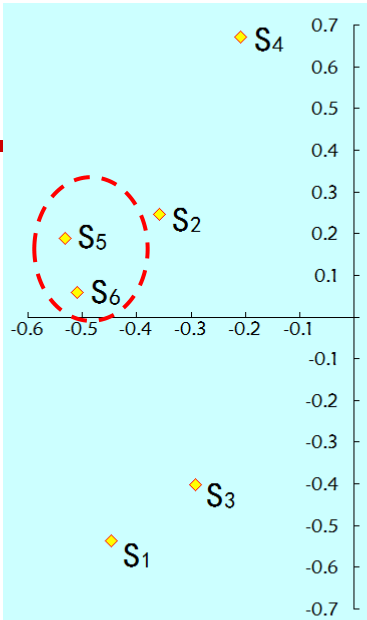
可以看到5号商品和6号的夹角很小,这两个很接近。
对V只取前两列并画图后就得到了用户的相似度,如下:
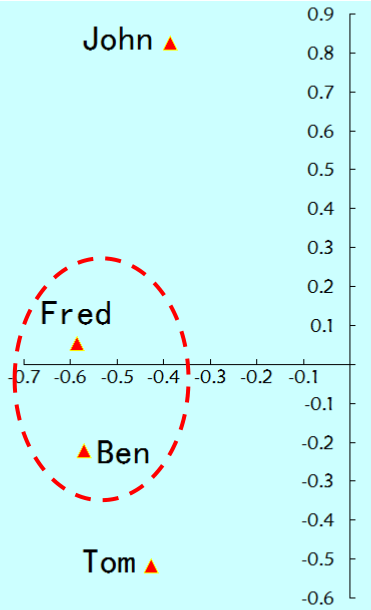
可以看到Fred和Ben是最接近的。
于是新来个用户时,如何对新用户进行个性化推荐呢?答案是:
1,还是那个例子,既然是新用户,那新用户就打分了,反馈到矩阵A就是多了一行。
2,对新的矩阵A做SVD分解,不过做SVD分解的话还是要费一定的气力的(需要求特征值和特征向量嘛),那怎么办呢?其实根据上面的图1就可以这么想:我算出新用户与其他用户的相似度后将新用户画到图1里,不就能找到与新用户最接近的用户了吗?那根据与新用户最接近的用户喜欢的东西,不就能给新用户推荐商品了。
2.1,于是首先通过如下的推导得到A=U∑VT中的V:
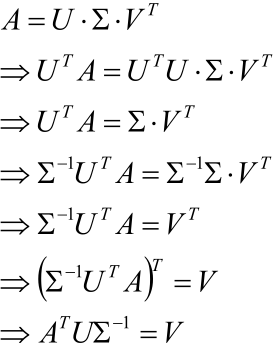
如:假设有个Bob的新用户,对6个产品的评分为(5,5,0,0,0,5)T,则:
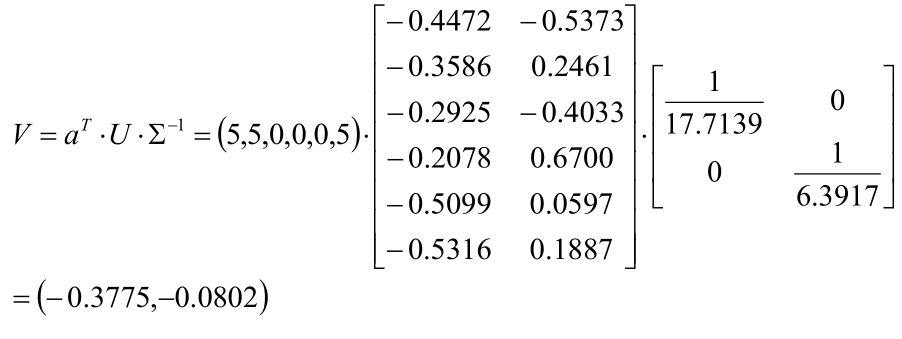
2.2,计算Bob与现有用户的距离(这里使用余弦距离)发现最近的是Ben,如下图:
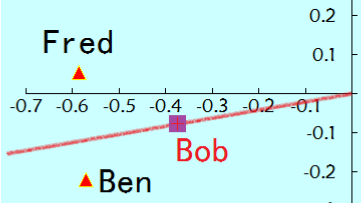
对比下Ben和Bob的打分:
Ben:5 5 3 0 5 5
Bob:5 5 0 0 0 5
因此,可顺序推荐S5和S3。
PCA总结
PCA与SVD的对比








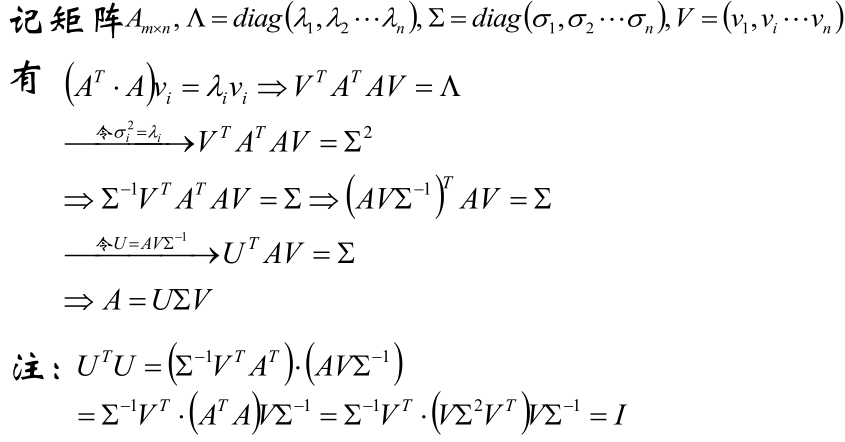















 1610
1610











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








